0 引言

　　被广泛应用的三相电压型逆变器是由多个全控型开关器件、二极管和滤波电感、电容等组成的一类时变的、耦合的、多输入多输出的非线性系统[1]，为方便控制，人们总希望将其化为线性系统。精确线性化这种非线性控制方法通过非线性坐标变换可将原来的非线性系统化为线性系统，从而将非线性系统的综合问题化为线性系统的综合问题[2]。经文献检索，该方法已被应用到Buck变换器、逆变器等电力电子变换器系统中[3-4]。在上述文献中，应用精确线性化得到的线性系统采用线性控制策略时，多结合最优控制方法。在选取二次型性能指标中的对称矩阵Q和R时，在文献[3]中采用经验矩阵数值，对怎样选取、如何选取并未给出依据；在文献[4]中选取的Q矩阵与系统的负载参数有关，一旦选取特定的Q矩阵，当负载参数发生变化时，采用原来反馈增益矩阵，系统的动态响应是否仍然较优值得商榷。如何选择反馈增益矩阵参数，减少其随机性是值得探讨的问题。

　　反步法是一种对带有参数严格反馈形式的非线性系统有效的设计方法，比较适合在线控制[5]。精确线性化得到的线性系统一般均可化为带有参数严格反馈形式模型，再对其采用反步法，比较容易得到系统的控制规律。本文将这两种方法结合起来应用于三相电压型逆变器系统中，并推导出一种非线性复合控制的模型，为逆变器的有效控制提供理论依据。

1 三相电压型逆变器的线性化分析

　　1.1 三相电压型逆变器的数学模型分析

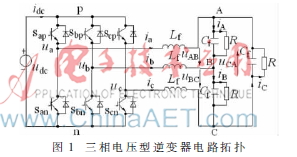
　　图1为三相电压型逆变器的电路拓扑，图中sij(i∈{a，b，c})，j∈{p，n})为全控型器件，Lf、Cf为滤波电感和电容，R为负载电阻。电路工作时每相桥臂中仅有一个开关器件导通，定义开关函数Si，当Si=1表示与p相连，Si=0表示与n相连。定义虚拟线电流iab=ia-ib，ibc=ib-ic，ica=ic-ia，线开关函数sab=sa-sb，sbc=sb-sc，sca=sc-sa。依据6个开关的8种状态和基尔霍夫定律可以得到[1]：

　　对于式(1)这样的多输入、多输出的非线性系统，存在uAB+uBC+uCA=0，iab+ibc+ica=0。式(1)中独立的微分方程数仅有4个，不妨取式(1)中的第1、2、4、5行。引入开关周期平均算子式(2)将式(1)离散系统变换为连续的系统[1]，其中TS为开关周期，x(t)为电路中的某电量。

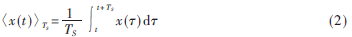
　　对式(1)求开关周期平均后，得到式(3)，式中各量均为开关周期平均值，为讨论方便，各变量仍保持原有书写格式。dab=da-db，dbc=db-dc，dca=dc-da为线间占空比。

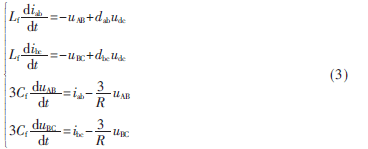
　　1.2 三相电压型逆变器的线性化条件验证

　　对于式(3)选取状态变量为x，控制输入变量为占空比d，输出变量为线电压y。具体含义为x=[x1 x2 x3 x4]T=[iab ibc uAB uBC]T，d=[dab dbc]T，y=[h1(x) h2(x)]T=[uAB uBC]T。系统的维数为4，式(3)对应的仿射非线性数学模型为式(4)：

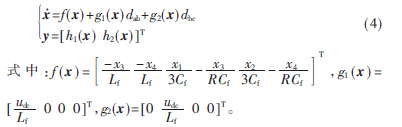
　　依据微分几何理论，如果满足下述2个条件则系统可实现线性化[2]：

　　(1)矩阵[g1(x) g2(x) adf g1(x) adf g2(x)]在x0邻域内的秩为4。

　　(2)下述4个向量场的集合在x=x0处每个都是对合的：

　　D1={g1(x)}，D2={g1(x)，g2(x)}，

　　D3={g1(x)，g2(x)，adf g1(x)}，

　　D4={g1(x)，g2(x)，adf g1(x)，adf g2(x)}。

　　对条件(1)的验证，通过计算李括号得到式(5)：

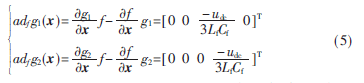
　　显然[g1(x) g2(x) adf g1(x) adf g2(x)]为对角阵，且与x无关，可以验证它在全局范围内的秩均为4。即条件(1)满足。将式(5)带入向量场D1、D2、D3、D4中，由于它们与x无关为恒向量场，任意两个恒向量场的李括号为零向量，因此D1、D2、D3、D4均是对合的，即条件(2)满足。当系统满足条件(1)和(2)时，可以选取一组输出函数实现系统状态反馈线性化。对输出h1(x)=x3，计算相应的李导数有：

　　根据上式计算的结果和系统相对阶的概念可知，对输出h1(x)的关系度为2[3]。对输出h2(x)=x4，计算相应的李导数，同理可得到对输出h2(x)的关系度为2。通过坐标变换可将原非线性系统转化成一个能控的线性系统。

　　1.3 精确线性化

　　令z1=h1(x)，z2=Lf   h1(x)，z3=h2(x)，z4=Lf   h2(x)，并对其求导可得到式(11)：

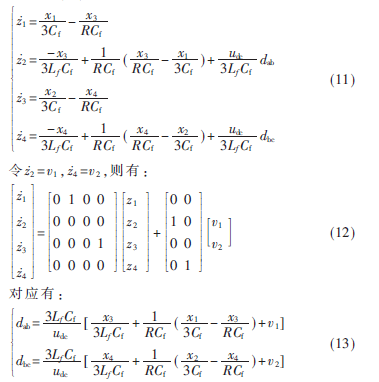
2 三相电压型逆变器的反步设计方法

　　将式(12)所示的系统模型写成具有参数严格反馈形式的多输入多输出非线性系统的一般表达式[2]：

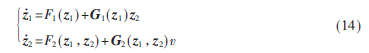
　　其中z1=[z1  z3]T=[x3  x4]T=[uAB  uBC]T，z2=[z2  z4]T，v=[v1  v2]T，F1(z1)=0，F2(z1，z2)=0，G1(z1)=I2×2，G2(z1，z2)=I2×2。系统的阶数为2，应用反步设计法时可按两步进行：

　　(1)定义系统跟踪误差相量矩阵E1为式(15)，式中z1ref为输出期望值。

　　对上式进行求导并整理后得到：

　　定义辅助误差相量E2矩阵函数为：

　　其中z2ref为虚拟控制相量。将式(17)代入式(16)中可得：

　　设计虚拟控制相量z2ref为：

　　式中k1=k11  00   k12为反馈增益矩阵，k11、k12为正实数。将式(19)代入式(18)得到：

　　对于式(20)，如果E2→0，则E1→0。

　　选取Lyapunov 函数为：

　　对式(21)求导，可得到：

　　(2)对式(18)求导得到：

　　设计控制相量v为：

　　式中k2=k21  00   k22为反馈增益矩阵，k21、k22为正实数。将式(24)代入式(23)得到：

　　选取Lyapunov函数为：

　　对式(26)求导可得到：

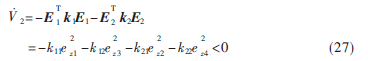
　　根据Lyapunov 第二方法可判定系统渐近稳定。

3 实验验证

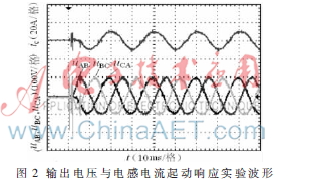
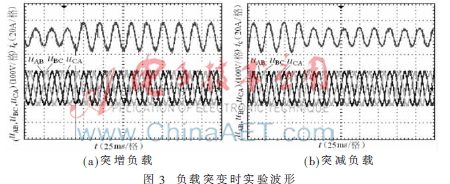
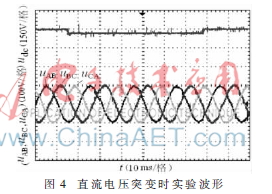
　　实验参数：给定三相对称输出电压峰值为100 V，输出频率设定为50 Hz，udc=150 V，TS=0.1 ms，R=20 ，Lf=5 mH，Cf=5 F。反馈增益选为：k11=k12=6 000，k21=k22=12 000。图2为起动实验波形，图3为负载突变时波形，负载由20 跳变为10 ，然后再由10 跳变为20 。图4为直流电压突变实验波形，其中直流电压变化范围为150 V→120 V→150 V。从实验结果可看出系统具有较好的动态、静态性能，对负载扰动、直流电压扰动具有较强的抗扰能力。

4 结论

　　本文将三相逆变器系统的仿射非线性数学模型，经过精确线性化得到具有参数严格反馈形式模型，再应用反步设计方法，推导出系统的控制模型。最后通过实验验证了该复合控制策略的有效性。

　　参考文献

　　[1] 徐德鸿.电力电子系统建模与控制[M].北京：机械工业出版社，2006：6-12.

　　[2] 胡跃明．非线性控制系统理论与应用[M]．北京：国防工业出版社，2005：188-193．

　　[3] 邓卫华，张波，胡宗波，等．CCM Buck变换器的状态反馈精确线性化的非线性解耦控制研究[J]．中国电机工程学报，2004，24(5)：120-125.

　　[4] 帅定新，谢运祥，杨金明，等.基于状态反馈精确线性化单相全桥逆变器的最优控制[J]．电工技术学报，2009，24(11)：120-126.

　　[5] YANG J H，WU J，HU Y M．Backstepping method and its applications to nonlinear robust  control[J]．Control and Decision，2002，17(S)：64l-647.