0 引言

    物理层网络编码通过在中继节点选择适当的调制解调技术，将相互叠加的电磁波信号映射为相应的数字比特流，然后进行异或处理（即进行了网络编码），使得所有多径、多播干扰变成网络编码的一部分，充分利用干扰来提高通信系统的性能^[1]。该技术自2006年提出以来就受到广泛关注^[2]。

    在同步条件下将物理层网络编码应用在无线中继系统传输中，可以使网络吞吐量比直接网络编码模式和传统中继转发模式分别提高50%和100%，信号传输速率也分别提高50%和100%^[3]，此外系统的抗干扰能力和安全性能也得到了提高。但在实际环境中，由于信道的距离、类型不同，以及不同终端之间振荡器、晶振频率等不可能做到完全同步，造成中继节点接收到的两个源节点信号存在载波相位偏移、载波频率偏移以及符号偏移，使得物理层网络编码的性能受到损失^[4-6]，因此研究各个因素对系统性能的影响具有重要意义。

    文献[7-9]从功率方面对系统性能损失进行理论推导和仿真实验，分析了各种异步条件对功率的影响。然而各种异步条件对系统误码率的影响一直缺乏相关理论。针对上述存在的问题，采用XOR的映射方式，在中继节点采用不同的处理方式，完成载波相位、载波频率偏移以及符号偏移对通信系统误码率的理论推导和仿真实验，为物理层网络编码的工程应用奠定理论基础。

1 系统模型

    本文考虑如图1所示的双向中继系统模型^[10]，首先两个源节点A和B同时向中继节点R发送信息(即多址接入阶段)，然后中继节点R对两个目的节点A和B(也就是源节点)广播信息。

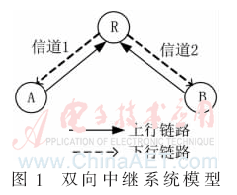
    在中继节点处理叠加信号的方法主要有：基于符号的叠加（Superposition，SUP）、基于排斥准则的近邻成簇（Closest-neighbor cluster，CNC）映射^[9]、基于码字的向量模加（Vector modulo addition,VMA）^[11]和基于比特的XOR等方法。其中基于比特的XOR方法最简单、最实用^[12]，因此在中继节点处采用XOR映射方式处理叠加信号。

2 影响因素及分析

2.1 载波相位的影响

    假设两发送信号载波相位差为θ，使用BPSK调制，则两源节点A和B发送的信号分别为：

    在中继节点处对叠加信号乘以载波2cos(wt)，通过低通滤波器得到信号：

    在相位偏移的条件下，物理层网络编码的映射关系如表1所示。

    由表1可知：在中继节点R处两个端节点的和信号a_A+a_B经过物理层网络编码映射之后分别得到-1和1，且-1和1的概率相等，均为50%。根据上述条件可得：

式中f代表映射函数，由贝叶斯公式和条件概率公式可以推导出：

式中，N₀表示噪声的方差。通过式(8)可以得到物理层网络编码映射的判决门限r₁和r₂，从而推导出在载波相位偏移的条件下中继节点接收信号的误码率公式：

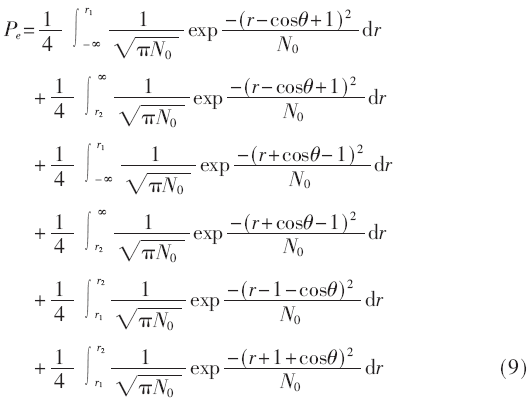
    图2是相位偏移θ分别为0、π/5、π/4和2π/5条件下信噪比随误码率的变化曲线。可以看出，随着载波相位偏移的增加，信噪比对误码率的影响越来越小。

    角度θ和信噪比对误码率的影响如图3所示。在图3的三维图形中可以发现，当载波相位偏移达到90°时，系统的误码率不再随着信噪比的变化而变化，而是趋于一个常数。因此，在物理层网络编码的工程应用中应尽量减少载波相位偏移。

2.2 载波频率的影响

    假设两个发送信号载波频率差为Δw，则两源节点A和B发送的信号分别为：

    从式(13)中得到，误码率和4个量有关系，分别是判决门限r₁和r₂、载波频率偏移Δw、帧数k和采样周期T。一般情况下取T=1，则误码率由r₁、r₂、Δw和k决定。

    当载波频率偏移较小时，假定取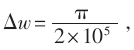则在SNR=5和SNR=10的条件下，可以得到帧数k对系统误码率的影响，如图4所示。

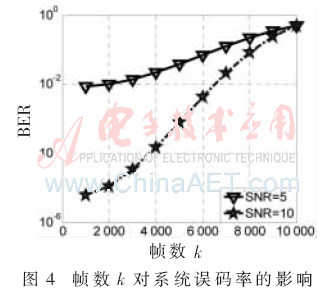
    通过图4可以得到，当载波频率偏移比较小的时候，随着帧数的增加，误码率逐渐提高，而且趋于一个常数。因此，在载波频率偏移比较小的条件下，应尽量减少帧数，以降低系统误码率。当载波频率偏移比较大的时候，需要把Δw·k作为整体考虑，将Δw·k的值整合到[0，π/2]之间，其对系统的影响和载波相位偏移对系统的影响相似。

2.3 符号偏移的影响

    假设两个发送信号时间同步误差为?Δt=εT(-1/2≤ε≤1/2)，则两源节点A和B发送的信号分别为： 

    在中继节点处对叠加信号乘以载波2cos(wt)，通过低通滤波器可以得到信号：

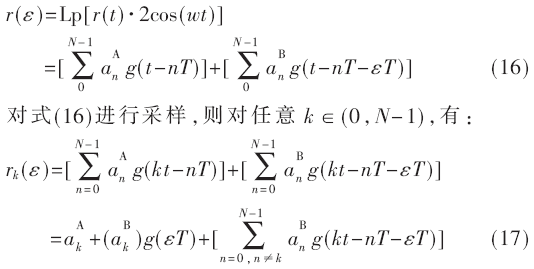
    由式(17)得到，时间不同步在降低了信号功率的同时，还引来了符号间干扰。

    为研究方便，取脉冲成形函数为升余弦滚降函数，即：

    在有符号偏移的情况下，物理层网络编码的映射关系如表2所示。

    使用和载波相位偏移类似的方法，得到：

    类似地可以推导出在符号相位偏移的条件下中继节点接收信号的误码率公式：

    图5是符号偏移ε分别为0、0.1、0.3和0.5条件下，信噪比对误码率的变化曲线。可以得到：在同一信噪比下，随着符号偏移的增加，系统的误码率逐渐升高。当符号偏移为0.5个符号时，系统的误码率达到最高，与同步条件(ε=0)下的误码率相比，最大相差6 dB。

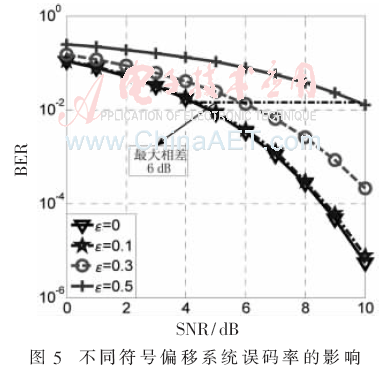
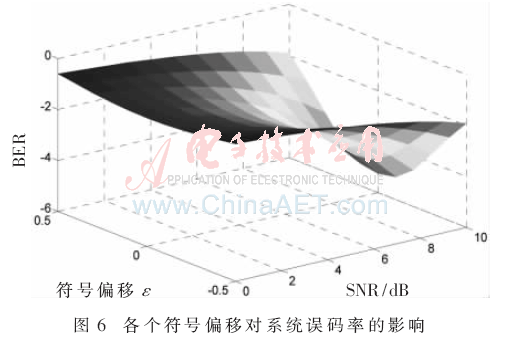
    图6为符号偏移和信噪比的变化对误码率的影响结果。由于g(t)是偶函数，因此图像关于ε=0对称。通过和图3对比可知，符号偏移对系统误码率的影响相对较小。

3 结论

    本文采用XOR映射方式首次从理论上分别得到载波相位偏移、载波频率偏移、符号偏移与系统误码率的数学模型。通过仿真实验可知，在同一信噪比下，随着载波相位偏移的增加，系统的误码率逐渐增加，当相位偏移达到最大值90°时，系统的误码率趋于一个常数，不再随信噪比变化。在载波频率偏移条件下，当偏移较小时，帧长的增加也会引起系统误码率的增加，当偏移较大时，系统性能受频率偏差和帧长共同作用。随着符号偏移的增加，系统的误码率相对于同步条件下最大损失6 dB，相比于载波相位偏移损失较小。本文通过理论推导和仿真实验，为后续的物理层网络编码工程误差分析建立了理论参考基础。

参考文献

[1] Zhang Shengli，Liew Soung Chang，Patrick P.Lam.Physicallayer network coding[C].The Annual International Conference on Mobile Computing and Networking(ACM Mobi-Com).2006：358-365.

[2] 赵明峰，周亚建，原泉，等.物理层网络编码研究进展[J].计算机应用，2011，31(8)：2015-2021.

[3] 陈志成.无线通信中物理层网络编码技术的研究[D].南京：南京邮电大学，2012.

[4] Lu Lu，Zhang Shengli.Asynchronous physical-layer network coding[J]．Wireless Communications，IEEE Transactions，2012，11(2)：819-831．

[5] Hao Yonggang，Goeckel Dennis，Ding Zhiguo，et al.Achievable rates of physical layer network coding schemes on the exchange channel[C].Proceedings of 2007 IEEE Mil Comm Conf，2007：1-7.

[6] Zhang Shengli，Liew Soung Chang，Patrick P.Lam.On the synchronization of physical-layer network coding[C].Proceedings of 2006 IEEE Information Theory Workshop，2006：404-408.

[7] Zhang Shengli，Liew Soung Chang，Wang Hui.Synchronization analysis in physical-layer network coding[EB/OL].[2011-01-11].http：//arxiv.org/pdf/1001.0069.

[8] Zhang Shengli，Liew Soung Chang，Wang Hui.Synchronization analysis for wireless TWRC operated with physicallayer network coding[C].Wireless Pers Commun，2013(68)：637-653.

[9] 宋欢，丁良辉，钱良.基于无线帧的物理层网络编码同步误差性能[J].信息技术，2013(9)：1-5.

[10] 苗金华.TWRC中物理层差分网络编码[D].天津：天津大学，2010.

[11] Nam Wooseok，Chung SaeYoung，Yong H Lee.Capacity bounds for two-way relay channel[C].International Zurich Seminar on Communications(IZS)，2008：144-147.

[12] Popovski Petar，Yomo Hiroyuki.Physical network coding in two-way wireless relay channels[C].IEEE International Conference on Communications，2007.