文献标识码: A
文章编号: 0258-7998(2015)06-0132-04
0 引言
在电磁波被发现不久,美籍科学家尼古拉·特斯拉便提出利用电磁波携带能量实现无线电能传输的构想[1]。无线电能传输分为电磁感应式、谐振耦合式和微波式[2]。谐振耦合式较于电磁感应式的传输方式传输距离得到了极大的提高[3];较于微波式的传输方式只有几毫瓦至几百毫瓦的传输功率[4],耦合式几十瓦甚至几百瓦的传输功率更为有效。谐振耦合式无线传输思想由MIT于2006年提出,2007年MIT利用电磁谐振原理在2 m多的距离处点亮了60 W的灯泡,且传输效率达到了40%左右[3]。
目前谐振耦合式无线电能传输仍处于起步阶段,在传输距离、传输功率和传输效率这三大要素方面的分析还不够[5]。文献[6]研究了传输功率、传输效率与负载的关系并利用功效积对系统进行了优化,但因忽略了接收线圈对发射线圈的影响导致最终理论与仿真结果悬殊较大。文献[7]考虑了接收线圈的影响,但未考虑到系统传输效率较大时传输功率较低的情况。分析传输效率和功率与负载等因素之间的关系,针对一些文献为了计算方便忽略了接收线圈对发射线圈的影响造成较大误差的问题,对比得出了接收线圈的影响是不可忽略的结论。同时利用功效积指标使系统优化解决了传输效率较大时往往功率不高的问题,并且对模型及参数进行了仿真验证。
1 谐振耦合式无线电能传输系统原理与模型
1.1 谐振耦合式无线电能传输原理
谐振耦合式无线电能传输系统原理性结构图如图1所示,包括发射端和接收端两部分。发射端由发射电路A和谐振线圈S组成,接收端由谐振线圈D和负载电路B组成。

系统工作时,激励线圈A产生高频磁场,源谐振线圈S在外加激励下谐振,能量由A传输到S,S通过磁谐振耦合将能量传给次级谐振线圈D,D再与负载电路B产生耦合将能量传输给负载。A、S、D、B 4个线圈均被设计成具有相同的谐振频率,在磁场的作用下可以产生谐振,但由于功能不同,各个线圈的其他参数不尽相同,如半径等[8]。
1.2 谐振耦合式无线电能传输电路模型
为了分析的简便,仅对发生谐振耦合的两收发线圈LS、LD进行等效分析,由于空心线圈在高频下的寄生电阻和寄生电容不能忽略,因此LS、LD的等效模型如图2所示。
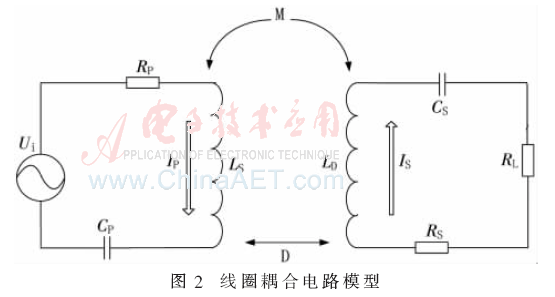
图2中,RP、RS为发射线圈和接收线圈内阻,为计算方便近似取RP≈RS;CP、CS为发射线圈和接收线圈补偿电容;Ui为加载在发射线圈上的激励,其频率为ω;RL为等效负载阻抗;M为线圈互感。
1.3 谐振耦合式无线电能传输数学模型
由于在传输过程中,接收电路肯定会对发射电路产生一定的影响,考虑这一因素后,根据图1,利用基尔霍夫定律可以写出回路方程组:

线圈传输效率是接收端负载上得到的功率和发射端的功率之比,即:
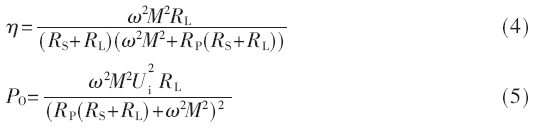
可见传输效率与功率均与ω、M、RS、RP、RL有关。当收发线圈参数一致时(即KS=KD)时:

其中,μ0为真空磁导率, r为线圈半径, d为传输距离,可见互感与 r、 n、 d有关。
高频下线圈损耗电阻主要包括欧姆损耗电阻RO和辐射损耗电阻Rr[9]:
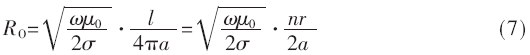
其中,a为导线半径;n为线圈匝数;σ为电导率;l为导线长度。
对于谐振耦合式无线电能传输系统,其谐振频率一般为1 MHz~50 MHz,此时有Rr<<Ro[9],即可忽略辐射损耗,则线圈损耗电阻Rp=Rs≈Ro。
2 系统分析与优化设计
2.1 系统最大功效积基本原理
一个系统中传输效率和传输功率是分不开的,但是大部分情况下很难使效率和功率同时得到最大值,于是引入功效积ψ这个概念,即功率和效率的乘积,当功效积达到最大值时,效率和功率均达到了较大值。由式(4)、式(5)得:

2.2 功效积与传输效率对比分析
随着负载的变化,效率存在最大值,即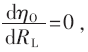 求解可得:
求解可得:

将式(12)代入式(4)和式(5)得(传输效率取最大):
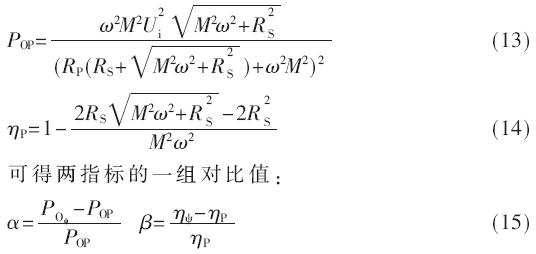
假设等效模型参数如表1所示。

根据表1的参数与式(10)~(11)、式(13)~(15)可得:α≈36%,β≈-9%。由α、β可知,最大功效积传输与最大效率传输相比,虽然效率下降了9%,但是功率上升了36%。综上所述,最大功效积相比较于最大效率传输具有优越性,对系统进行了优化,实现了较高传输效率的同时拥有较高的输出功率。
2.3 与忽略接收线圈系统的对比分析
一些文献为了研究方便忽略了接收电路对发射电路的影响,使理论推导进一步简化。
根据文献[7]中的公式与表1参数得:当忽略接收线路对发射线路影响时,最佳负载RL≈13.3 Ω。
由式(9)得,当考虑影响因素时,最佳负载RL≈17.5 Ω。
对比上述两种情况可得,忽略接收线圈影响与不忽略影响的最佳负载误差约为32%,误差很大,可证明接收电路对发射电路的影响不可忽略。
3 仿真结果与分析
3.1 不忽略接收线圈影响的仿真分析
由上文可知,功效积为最大时,负载约为17.5 Ω。运用MATLAB软件对图1仿真得出对应的输出电流、输入电压和输入电流如图3~图5所示。
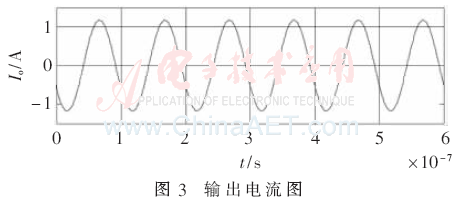
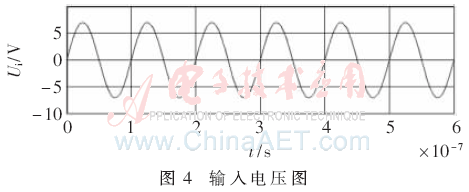
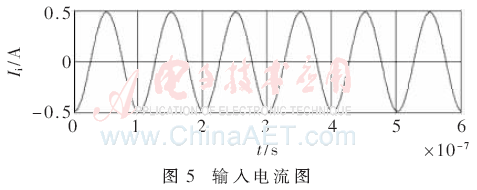

当负载分别7.5 Ω、12.5 Ω、17.5 Ω、22.5 Ω、27.5 Ω时,分别仿真得到对应的输出功率、效率和功效积,再根据式(4)、(5)、(8)计算出对应的输出功率、效率和功效积,理论数据和仿真结果如表2所示。
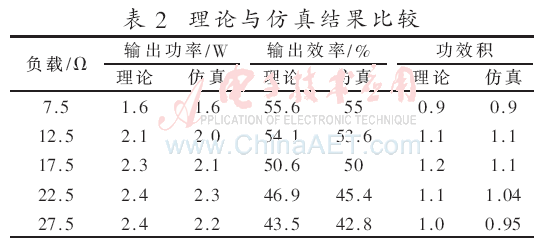
由理论分析可知:负载为17.5 Ω时,功效积达到最大。且由表2中几组仿真数据对比可知,当负载为17.5 Ω时,功效积最大。从表2可以看出,理论与仿真的结果基本吻合,而且当功效积最大时,可以同时保证较高的输出功率和效率,从而论证了功效积的优越性。但是理论与仿真还是存在一定差距,是因为理论分析十分理想化并且忽略了线圈的辐射损耗电阻,而且仿真过程中很多参数设置为近似数所导致的。
3.2 忽略接收线圈影响的仿真分析
当忽略接收电路对发射电路的影响,取负载13.3 Ω时,运用MATLAB软件可得仿真结果如图6~图8所示。
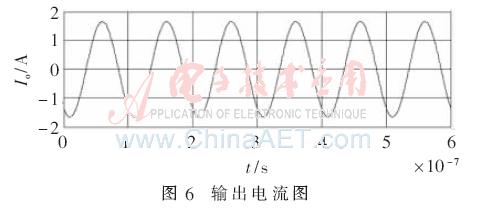
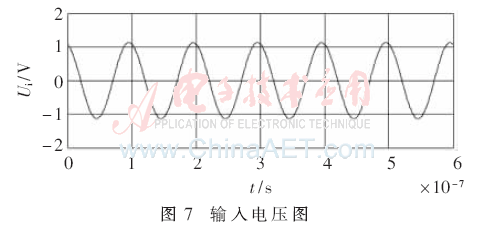
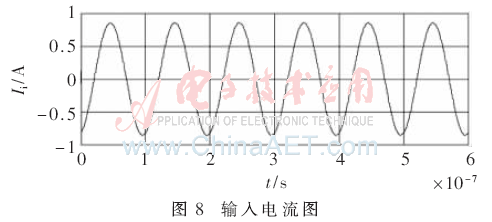
由图6~图8可得仿真结果ηD=82%,PD=4.8 W。
由表1的参数与式(14)得,不忽略接收线圈影响的最大传输效率为55.7%,与ηD对比再次印证了接收线圈对发射线圈影响的不可忽略性。
4 总结
本文利用互感等效模型分析了影响输出效率和功率的因素。得出了以下结论:
(1)忽略接收线圈的影响后,最佳负载的误差达32%,且传输效率仿真结果为82%,远高于理论最大值55.7%,证明了接收线圈的影响是不可忽略的。
(2)功效积为最大时的传输效率虽然比传输效率最大值低了9%,但输出功率却比效率最大时上升了36%,说明了功效积对系统确实进行了优化。
(3)仿真结果与理论数据误差在3%左右,而忽略接收线圈影响的误差为32%,说明了理论分析过程的优越性。
参考文献
[1] LI H L,HU A P,COVIC G A,et al.Optimal coupling condition of IPT system for achieving maximum power transfer[J].Electronics Letters,2009,45(1):76-77.
[2] 黄静,邵兵,王剑飞.无线电能传输系统参数优化[J].电子技术应用,2014,40(12):28-31.
[3] 汪强,李宏.基于磁耦合谐振的无线电能传输系统的研究[J].电子技术应用,2011,37(12):72-75.
[4] YOUNDO T,JONGMIN P,SANGWOOK N.Mode-based analysis coupled of resonant characteristics for near-field small antennas[J].IEEE Antennas and Wireless Propagation Letters,2009(8):1238-1241.
[5] JIN W K,HYEON C S,KWAN H K,et al.Efficiency analysis of magnetic resonance wirelesspower transfer with intermediate resonant coil[J].IEEE Antennas and Wireless Propagation Letters,2011(10):389-392.
[6] 张智娟,董苗苗.谐振式无线电能传输系统的研究[J].电子技术应用,2013,39(8):54-56.
[7] 傅文珍,张波,丘东元,等.自谐振线圈耦合式电能无线传输的最大效率分析与设计[J].中国电机工程学报,2009,29(18):21-26.
[8] 郑盼龙,迟冬祥.一种小型磁谐振式无线电能传输系统的实验研究[J].机电工程,2014,31(10):1333-1338.
[9] KURS A,KARALIS A.Wireless power transfer via strongly coupled magnetic resonances[J].Science,2007,112(6):83-86.

