摘  要： 传统FCM聚类算法存在初始聚类中心较为敏感的问题，易陷入局部最优。针对此问题，提出了基于密度权值和自适应免疫系统的FCM算法（d-AIFCM）。算法在对Web用户进行聚类分析的过程中，基于用户群体之间的相似性，引入密度权值生成候选初始聚类中心，采用自适应免疫系统的原理确定初始聚类中心，自动生成最佳分类，解决传统FCM算法对初始聚类中心敏感的问题。实验结果表明，d-AIFCM算法在收敛次数和聚类效果方面较其他同类算法有所提升。

　　关键词： 初始聚类中心；FCM；自适应免疫算法；Web用户聚类

0 引言

　　在互联网高速发展的时代，Web服务的方式趋于多元化，如何为不同需求的Web用户提供个性化服务是当前网络服务的研究热点。目前，多个研究小组通过对Web用户进行聚类分析，研究用户的行为、兴趣等信息，从而为用户提供个性化服务。在实际应用中，用户的兴趣受多方面影响，采用FCM进行聚类分析能较客观地反映现实世界。本文对传统的FCM算法进行改进，并将其应用于Web用户聚类分析，具有一定的研究意义。

1 相关工作

　　FCM算法对初始化数据较敏感，易陷入局部最优。针对该问题有两种解决办法：一种是在聚类过程中进行全局随机搜索，参考文献[1]利用模拟退火算法扰动当前聚类结果，扰动结果以一定的概率被认为是当前的全局最优解，但计算耗时长。另一种是改善初始化条件，参考文献[2]提出的FaiNet算法利用生物克隆免疫系统的原理对原始数据进行初始化，但其初始抗体群是随机生成的；参考文献[3]利用参考区域获取聚类中心，算法的性能依赖于区域半径的选取。本文引入密度权值，将自适应免疫原理与FCM算法结合提出d-AIFCM算法，该算法可自动生成最佳分类，解决了FCM算法对初始聚类中心敏感的问题，能够最大程度找到全局最优解。

2 算法设计

　　2.1 用户兴趣矩阵

　　设pj为网站页面，ui为访问用户，则ui对pj的兴趣度Iij为：

　　其中，ω表示ui对pj的浏览次数，Tijt表示ui第t次访问pj的浏览时间。

　　定义1 （用户兴趣矩阵）以pj为横坐标，以ui为纵坐标，以Iij为矩阵元素构造用户兴趣矩阵：

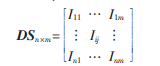
　　2.2 算法思路

　　设DS为样本数据集合，D为样本的密度权值；RS为候选初始聚类中心集合；MS为初始聚类中心集合。

　　2.2.1 确定候选聚类中心

　　聚类中心处于所代表类的中心位置，且在样本点密度连续的范围内应该只具有一个聚类中心，以防止两个类高度重叠。故聚类中心的选取应该满足：具有较高的密度且与其他中心的距离尽可能大。

　　本文对每一个样本点赋予密度权值：

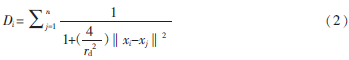
　　其中，‖xi-xj‖2为样本点间的欧氏距离，rd表示领域密度半径：

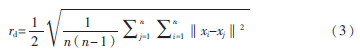
　　2.2.2 确定初始聚类中心

　　自适应免疫系统是人体的重要防御系统。当机体受到抗原性异物刺激时，被激活的抗体会发生选择性克隆与变异，部分与抗原具有较高亲和力的个体保存并组建成为该抗原的记忆细胞。受自适应免疫系统的启发，抗体的克隆过程相当于用户兴趣的传播过程，变异过程相当于用户的兴趣变化，记忆细胞类似于聚类中心。将RS中的元素Ri视为抗体，DS中的元素Gj视为抗原，产生的记忆细胞即为初始聚类中心。

　　定义2 （亲和度）亲和度用来衡量抗体与抗原之间的匹配性，用τij表示：

　　定义3 （克隆）克隆是抗体进行的自我复制过程，其克隆体的数量为：

　　定义4 （变异）变异是抗体在克隆过程中为增加个体多样性而进行的操作，变异公式如式（6）所示：

　　Ri=Ri-α（Ri-Gj）（6）

　　其中，α表示变异率，计算公式为：

　　其中，r为[0，1]之间的随机数，，DGj表示抗原Gj的密度权值。

　　2.2.3 算法实施

　　d-AIFCM算法的具体实施过程如下：

　　（1）选取候选聚类中心。

　　输入：DS

　　输出：RS

　　①初始化样本密度权值D；

　　②选取拥有最大密度权值的样本点xi，RS←xi，Set←xi，从DS中移除xi；

　　③选择与xi最近的样本点xl，Seti←xl，从DS中移除xl；

　　④选取xk，xk与Set中的样本点距离最近；

　　⑤如果Dk小于Set中所有样本点的密度权值，从DS中移除xk，转到步骤④，否则转至步骤②；

　　⑥输出RS。

　　（2）确定初始聚类中心。

　　输入：DS，RS

　　输出：MS

　　初始阈值σ、ε；

　　For Gj in DS；

　　If Gj与MS中的记忆细胞的距离大于ε；

　　计算RS中抗体Ri与抗原Gj的亲和度；

　　选取亲和度最大的前n个抗体→RS′；

　　For Ri in RS′

　　Rit=Ri-α（Ri-Gj）

　　End for

　　End for

　　计算Rit与Gj的亲和度，按一定比例保留亲和度较大的克隆体→MS′；

　　计算MS′中克隆体之间的欧式距离，删除距离小于阈值σ的克隆体；

　　计算MS′的重心，得到记忆细胞M，M→MS；

　　End if

　　End for

　　（3）以MS中数据为初始聚类中心执行FCM算法的迭代过程。

3 实验结果与分析

　　3.1 实验数据与环境

　　实验数据：实验数据采用某学院网站2012年1月份一周内的Web日志，对Web日志进行预处理，处理后共有2 786个用户，28个网站页面。

　　实验环境：Intel（R）Core（TM）i3-3210M@3.20 GHz CPU，4 GB内存，Windows XP 32位操作系统。采用JAVA实现算法，并利用MATLAB制作实验图表。

　　3.2 评价指标

　　实验分别从迭代次数（I）、分支系数（PC）[4]和分配熵系数（PE）[5]对本文算法、原始的FCM算法以及参考文献[3]的FaiNet算法进行了比较分析。

　　PC值反应了模糊集群之间成员共享的程度，值越高，集群之间的重叠就越小，计算公式为：

　　PE是验证模糊聚类的另一个指标，值越小，算法就越稳定，计算公式为：

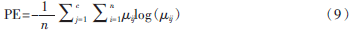
　　3.3 实验分析

　　在本实验中，FCM算法中的加权指数b取值为2，阈值σ取0.18~0.98共9个值，进行9组实验。实验过程发现，类别数与σ相关，σ越小，产生的记忆细胞数越多，类别数越多，反之亦然，如图1所示。

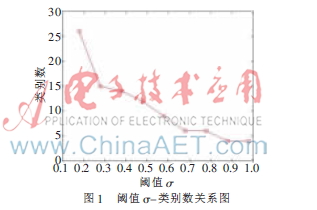
　　3.3.1 迭代次数的比较

　　FaiNet算法中的抗体群是随机生成的，属不完全匹配的记忆细胞法。d-AIFCM算法在进行聚类之前已经充分考虑密度权值和距离等因素，又经过克隆和变异操作，挑选出一批较精确的初始聚类中心，类别数也随之确定，属完全匹配记忆细胞法，避免了原始FCM算法随机选取初始聚类中心的弊端，这样可以加快聚类过程的收敛速度。可以通过实验来进行验证，实验结果如图2所示。

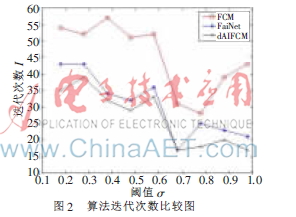
　　3.3.2 PC和PE的比较

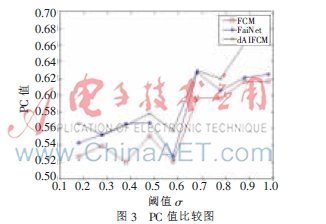
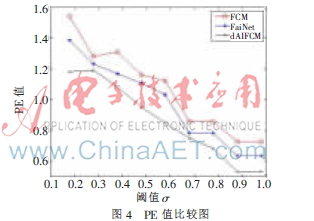
　　PC值和PE值的对比分别如图3、图4所示。从图3及图4可知，d-AIFCM算法具有较小的重叠性和较大的稳定性。同时，算法的PC值呈上升状态最后趋于平稳，PE值呈下降状态最后趋于平稳，说明当类别数越多，针对用户的分类越详细，一个用户所归属的类别数也越多，则类间的重叠性就会增加；当类别数越少，分类结果趋于平稳，极端情况下，所有用户同属于一个类，则重叠性最小且最稳定，但是这不符合实际情况，故在实际应用中应根据实际的需要选择合适的σ值。

　　可以注意到，实验中阈值σ取不同的值时，PC值的跳跃性较大，且PE值明显均较高，这与数据集的特性有关，数据集是从实际的Web日志中提炼出来的，数据稀疏性较大，可能影响算法的性能。

4 结论

　　本文针对FCM算法中存在的对初始聚类中心敏感的问题，在自适应免疫算法的启发下，提出了一种新的基于Web日志的聚类方法。该方法无需人工作指定类别数，类别数可在算法实施过程中自动生成，并减轻了数据初始化对聚类结果的影响。实验表明，该算法与相关算法相比，在收敛次数和聚类效果上具有一定的优越性。在后续的工作中，将围绕如何降低数据稀疏性对算法性能的影响等方面展开。

参考文献

　　[1] Zhao Xinchao. Simulated annealing algorithm with adaptive neighborhood[J]. Applied Soft Computing， 2011，11（2）： 1827-1836.

　　[2] SZABO A， DE CASTRO L N， DELGADO M R. FaiNet： an immune algorithm for fuzzy clustering[C]. Fuzzy Systems （FUZZ-IEEE）， IEEE， 2012： 1-9.

　　[3] 李鑫，张继福，蔡江辉.一种基于大密度区域的模糊聚类算法[J].小型微型计算机系统，2012，33（6）：1310-1315.

　　[4] Xie Xuanli， BENI G. A validity measure for fuzzy clustering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1991， 13（8）： 841-847.

　　[5] AMIG?魷 E， GONZALO J， ARTILES J， et al. A comparison of extrinsic clustering evaluation metrics based on formal constraints[J]. Information Retrieval， 2009， 12（4）：461-486.