摘  要： 四旋翼飞行器的制作与研究日渐火热，而且其应用价值日渐凸显，当今四旋翼飞行器大都使用飞控板控制，其优点是操作简单，稳定性比较好，但很多的复杂功能无法自定义，仅仅能使用其固有的动作。源于市面上飞控板的这一不足，设计了具有自主特色的控制思路，重点讲解在研究过程中的角度平衡的数据处理思路与方法。

　　关键词： 四旋翼飞行器；平衡；陀螺仪；加速度计

1 四旋翼飞行器结构框图与描述

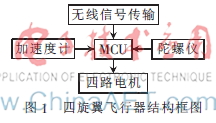
　　该飞行器由一主控MCU从传感器读取加速度计输出的重力加速度模拟量与陀螺仪输出的角速度模拟量，对其进行比例融合相互补偿获得真实的角度值，以备主控控制电机的转速来保持平衡。图1为飞行器简略结框图。得到准确的角度值是控制平衡的关键之处。当前市面上购买的飞控板大都采用卡尔曼算法和互补算法，对比这些算法可谓各有利弊，但这些算法也都是对模拟量进行滤波融合。

2 角度值输出误差的问题与发现

　　角度值是控制平衡核心参考量，MCU对传感器的模拟量进行读取，而后将当前加速度计模拟量G和陀螺仪模拟量A分别减去各自固定的常数（平衡点重力加速度GK、平衡点角速度常数AK），得到当前的净输出重力加速度GO和净输出角速度AO，再经过滤波算法对当前GO和AO比例拟合得到当前角度Aangle。此处最关键点在于GK、AK这两个常数的确定，它们的准确与否直接影响到角度Aangle的正确与否。计算角度过程中，常用的思想就是事先测试出一个合适的静态AK，然后将当前从陀螺仪读取来的A减去这个静态AK得到净输出角速度值AO。将AO进行积分得到理论角度值，然后将从加速度计读取到的G减去测试出来的静态GK得到净输出GO，而后用得出的GO按一定权重（1/T）去补偿角速度积分出来的角度值，最后将补偿后的角度值乘以一个固定常量比例值（S），便可以得到当前角度值Aangle。图2为角度融合的总体流程框图[1-2]。

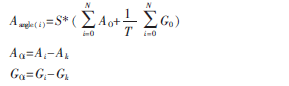
　　但由于陀螺仪与加速度计温移比较严重，因此平衡零点模拟量无法准确确定，而且陀螺仪静止时角速度输出噪声（如图3所示），更进一步加大了平衡零点确定的难度系数。

3 动态平衡零点常数的引入

　　通常采用静态平衡点常数来计算当前角度，其弊端是当环境温度变化时便无法输出正确角度值。针对静态平衡点适应性差的问题，动态设定平衡点的思想还是很有必要的。所谓动态平衡点就是飞行器在起飞之前维持其处于水平且静止状态，然后读取当前的加速度计和陀螺仪输出模拟量读取N次求平均值之后将其设定为平衡点常数GKt、AKt，而后便可以稳定起飞。

　　其中，Gt为当前读取的重力加速度计模拟量，At为当前读取的陀螺仪输出模拟量。

4 动态平衡零点设定的优化

　　当飞行器刚上电，系统各种电路模块不够稳定导致电源电压出现波动，此时的输出模拟量存在一定偏差，动态平衡点确定是要求飞行器各个电路模块要处于稳定状态，所以要求在上电之后稍作延时再设定平衡点常数GK、AK。当各个电路模块稳定以后，对模拟量的读取常用的方法是取N次便设定为平衡零点模拟量，因为在角度值的确定过程中角速度起主导作用，其输出偏差大小很大程度影响到计算的角度值，而重力加速度值只是用来修正和补偿计算角度值的，这里不作过多讨论，重点放在角速度积分环节上。

　　图4为不同时刻读取N次角速度均值输出波形。

　　从图4可以看出AK（1 630，1 645），显然动态AK是一个范围值，而非确切值。当设定值为最高点AK=max（1 630，1 645）时，积分不久之后便会使计算角度再次偏大，当设定值为最底点AK=min（1 630，1 645）时，积分不久之后便会使计算角度再次偏小Aangle（i）<Aangle实际，使飞行器失去平衡而至炸机。因此动态AK的设定存在一定的偶然性。可以看出加速度计在静止时会围绕某一个固定值（此处大约为1 637）上下波动，所以对现在输出平均模拟量进行累加之后再求一次平均值，便可以得到要得到的最近似平衡零点，如图5所示，其中水平线为比较理想Ak。

5 优化后的角度跟随图像分析

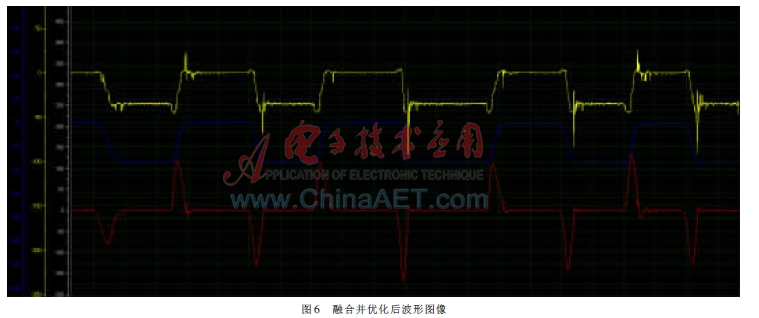
　　融合并优化后的波形图像如图6所示，其从上到下波形依次为净输出重力加速度GO，融合之后的实际角度Aangle，净输出角速度AO。

6 结论

　　在使用模拟量加速度计和陀螺仪计算角度值时，动态平衡常数有其存在的必要性，动态平衡常量解决了静态平衡点适应性差的缺点，但动态平衡常量的引入也带来了一定的弊端，其使得平衡常量值是一个范围值而非确切数值，解决办法是适当提高平衡常量设定时对模拟量的读取次数，多次读取求平均值能使得平衡常量更加逼近最优常量值，从而得到更精确的角度值。

参考文献

　　[1] 邹伯敏.自动控制理论（第三版）[M].北京：机械工业出版社，2007.

　　[2] 智能车竞赛秘书处.电磁组直立行车参考设计方案（版本2.0）[Z].2012.03.