0 引言

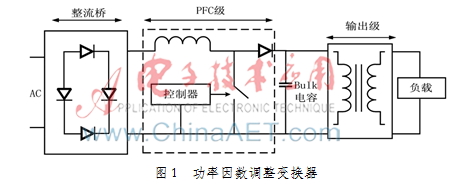
　　目前开关电源的功率因数都需要满足各种国际国内标准，为了满足功率因数的要求，需要设计功率因数校正电路。其中带有APFC电源驱动的设计中通常都是在桥式整流与DC-DC中间加上功率因数(PF)校正电路，正如图1所示[1]。该部分电路可以工作在CCM、DCM、CRM 3种导通模式下。对于输出功率小于100 W的系统优先选择CRM导通模式，CRM导通模式可实现ZCT-Boost，可有效地降低开关损耗和开关应力，也可以降低EMI干扰。

　　由于现有的论文里绝大部分是对电流控制模式和电压控制模式中CCM和DCM的研究[2-6]，极少有关于CRM下小信号建模的研究，尤其是在电压控制模式下。因此本文着重对电压模式下CRM-Boost-PFC的小信号建模进行详细的分析和推导，并由此推导做出了对应的补偿器的设计。最后用一个10 W Boost-PFC设计实例验证了小信号分析及补偿设计的合理性。

1 电压型控制模式的优缺点

　　开关电源IC的系统设计中控制形式的确定很重要。由于电压控制模式和电流控制模式有着明显的结构区别，它们也有各自的特点。

　　电压控制模式是最早在稳压电源设计中采用的方法，这种设计的主要特性是只存在一条电压反馈通路，而脉宽调制是通过将放大的误差电压信号与斜波信号进行比较来完成的，过流检测必须单独执行。因此电压控制模式拥有如下优点[2]：

　　首先它采用单个反馈环路，因而比较容易设计和分析。其次它用一个大幅度斜波提供了用于实现稳定调制过程中充分的噪声裕量。除此之外，低阻抗功率输出为多输出电源提供了更加优良的交叉调制性能。与电压模式相比，电流模式对上述缺点都有所优化，但又引入了新的问题，例如增加了反馈环路数量后补偿变难，当占空比大于50%时，需要采用斜波补偿的方法来稳定环路等。如果对电压控制型的缺点加以改善，例如加入电压前馈来采样输入电压，正如UCC3570。改进后它会拥有巨大的优势。

2 电压控制模式的CRM-Boost PFC工作原理

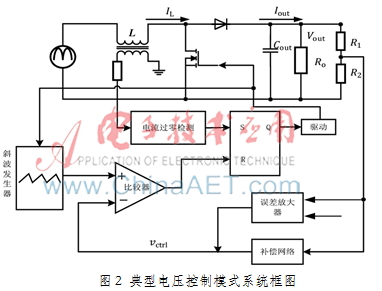
　　图2为电压控制型升压转换器的系统框图，由图可看出，典型电压控制模式的IC没有乘法器，且只有一个电压控制回路。电压控制型有输出电压采样和零电感电流采样，不对输入电压采样。因此电压控制模式适合于系统对动态响应要求不高且带恒定负载的开关电源中。

　　图2的电压控制系统通过采样网络R1和R2对输出电压采样，采样后信号送入误差放大器的反相端，其正相端为参考电压，误差放大器和补偿网络放大的误差信号与斜波信号进行比较的结果送入RS触发器的R端。RS触发器的S端接收电感/电流检测信号的触发，RS触发器的输出送给驱动器使功率开关管工作。

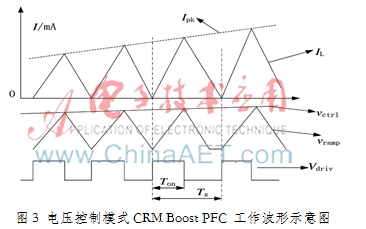
　　正常工作时如图3所示，功率开关管只有在电感电流为零时才开通，且Vramp也只有在电感电流为0时才开始上升。只要Vramp上升至Vctrl，功率开关管会立即被断开。

3 小信号模型推导

　　电压控制模式下的功率开关管工作在恒定导通时间且变频的工作状态，传统的态空间平均法来已不再适用。只能采用电流注入等效电路的方法来建立其数学模型[7-8]。在小信号模型分析之前先假设：

　　(1)变换器中的电感和电容都是理想元器件。

　　(2)变换器中的功率开关管和二极管是理想元器件。

　　(3)输出Cout电容产生的电压纹波足够小。

　　(4)功率级输入电压Vin(t)在一个开关周期里是恒定的，Vm为其峰值。Ts相对于TL足够小。

　　对于Boost-PFC，在单个开关周期，传输到输出二极管的平均电流为：

　　其中Ddis为放电时间占空比，对于临界导通模式，Ddis为：

　　整理可得：

　　因此，半个AC周期的平均值为：

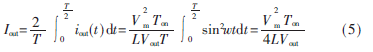
　　分别对Ton、Vout、Vm求微分运算再求和：

　　令。因此该系统功率级的小信号等效电路可用图4表示。

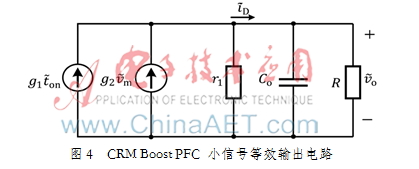
　　假设Vctrl与Ton的关系为K=ctrl/Ton。因此：

4 补偿设计实例

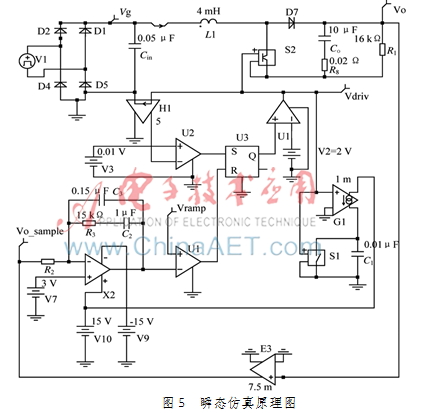
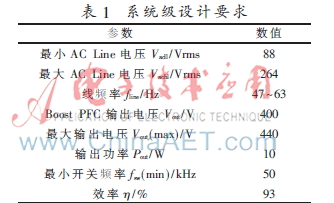
　　该设计系统级要求如表1所示，其原理图如图5所示。本文的第3节已经对该类型控制电路做了小信号分析，得到了输入到输出和控制端到输出的传递函数，为补偿的设计做了理论分析。要使补偿后的系统稳定，需满足以下条件[9]：首先要静态误差电压为足够小；其次要补偿后相位裕量至少为45°；最后系统的穿越频率为线电压频率的1/5~1/10。

　　首先对要建立的开环系统进行补偿前AC仿真，没有补偿网络时，仿真结果如图6。从该波特图中可以看出，相位裕度满足要求，但系统的穿越频率太高，无法对输入电压中100 Hz的纹波进行抑制，不满足设计要求，因此要加补偿网络使系统得到优化。

　　设定控制IC的系统要求当Vctrl变化量在1 V~4 V时，导通时间Ton变化范围为0.5 μs~12 μs。因此开环情况下，由系统参数规格确定输入到输出和控制到输出的传递函数为如下：

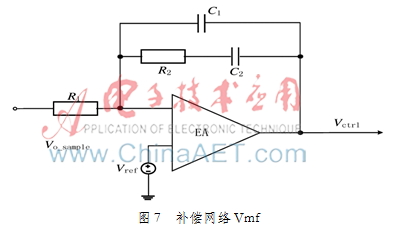
　　由于开环控制环路只有一个低频极点，所以选择Ⅱ型补偿，如图7所示。该结构提供一个抵消低频极点的零点，再给环路一个零频率极点和高频极点[9]。低频零频率极点可以提高低频增益，改善静态误差；低频零点提高相位裕量，增大阻尼，降低超频和调节时间；高频极点可提高降噪性能。

　　该补偿网络的传递函数如下：

　　由系统控制到输出的传递函数确定的补偿方案如下：

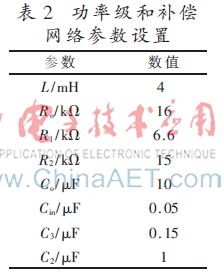
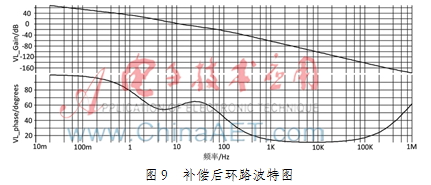
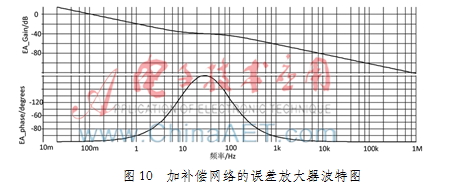
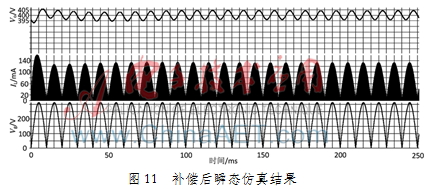
　　通过计算，该CRM-Boost-PFC功率级参数和补偿网络的参数如表2所示。最后通过建立如图8所示系统的小信号模型，并进行AC分析，得到如图9补偿后环路波特图和如图10带补偿网络的误差放大器的波特图。通过仿真可以看到，通过补偿后的环路，其相位裕度为52°，穿越频率为12 Hz。系统稳定且对100 Hz的纹波有很好的抑制作用。确定补偿网络后又对整个系统做了瞬态仿真，结果如图11。整个系统启动140 ms后完全稳定了下来，输出电压的纹波控制5 V以内，达到了设计的目的。

5 结论

　　本文针对工作于变频状态的电压控制型CRM导通模式的Boost PFC转换器进行了小信号分析，在状态空间平均法不适用的情况下用电流注入等效电路法进行了小信号建模，并给出了合理的补偿设计方案；在SiMetrix/SIMPLIS仿真平台下进行了实例设计，通过该设计验证了该小信号分析方法及补偿设计的合理性。该方法不仅对变频系统板级的分析与设计有重要的意义，也对变频系统的控制芯片系统级设计有重要的指导作用。

参考文献

　　[1] TYRCHI J.ON semiconductor application note AND8123/D，power-factor correction stages operating in critical conduc-tion mode[EB/OL].(2003-09)[2014-07].http：//www.onse-mi.cn/publink/collateral/AND8123-D.PDF

　　[2] MAMMANO R.UNITROOE design note DN-62，switching power supply topology voltage model VS currentmodel[EB/OL].(1999-09)[2014-07].http：//www.ti.com/lit/an/slua119/slua119.pdf.

　　[3] SEBASTIAN J，JAUREGUIZAR M，UCEDA J.An overview of power factor correction in single-phase off-line power supply system[C].Proc.Of IEEE IECON 1993：1688-1693.

　　[4] Zhang Xiangjun，Wang Binze，Ding Hao，et al.Study of CCMBoost PFC based on Simulink[C].IEEE IPEMC 2012：1756-1760.

　　[5] Yang Sungpei，Chen Shin-Ju，Huang Chaoming.Small-Sig- nal modeling and controller design of BCM-Boost-PFC converters[C].IEEE Conference on Industrial Electronics and Applications(ICIEA)，2012：1096-1101.

　　[6] RIDLEY R B.A new continuous-time model for current-mode control with constant frequency，constant on-time，and constant off-time，in CCM and DCM[C].IEEE PESC 1990：382-389.

　　[7] TANG W，LEE F C，RIDLEY R B.Small-signal modeling of average current-mode control[C].APEC′92，1992：747-755.

　　[8] CHETTY P R K.Current injected equivalent circuit approach(CIECA) to modeling of switching dc-dc converters [J].IEEE Trans.Aerosp.Electron.Syst.，1982，IE-29(3)：230-234.

　　[9] PRESSMAN A I.开关电源设计(第三版)[M].北京：电子工业出版社，2010.