文献标识码: A
文章编号: 0258-7998(2015)01-0107-04
0 引言
图像置乱技术是当前主流的图像加密技术,众多研究者已提出了具有良好的置乱性能的图像置乱算法[1-5]。但是对于图像置乱性能(置乱度)的评价研究却相对滞后,大部分依赖原始图像,如文献[6-8]等,缺乏统一的标准和模型。图像置乱度评价应重点研究根据图像各种特征建立科学的模型,并从模型出发设计具体评价指标,最终形成较完善的、能够独立于原始图像的盲评价指标体系。图像特征模型的建立有两种方式:(1)根据自然图像特征建立自然图像的特征模型;(2)基于理想置乱图像建立特征模型。前者需对大量自然图像特征进行统计分析,工作量大。后者所依据的理想置乱图像实际上是不能得到的,因此只能根据实际置乱图像的特征对理想置乱图像特征进行拟合,来建立模型。
在文献[9]中对置乱图像差分直方图的分布特性进行了详细分析,指出在理想置乱情况下,置乱图像的差分直方图应服从线性分布,并给出了相应的线性模型:
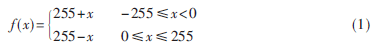
该模型是一个线性分段函数,自变量x为差分值,函数值为图像差分值个数。该模型表明:理想置乱情况下,置乱图像的差分直方图统计分布曲线是以差分值为自变量的分段线性函数。该模型的提出使得针对图像差分的置乱度评价工作有了科学的模型。但只是根据大量实验数据的分布特性,主观确定了该线性模型,并未进行科学、详细的证明。本文以此为出发点,采用统计分析方法,将此问题转化为分布函数的拟合检验和回归分析问题,通过建立线性回归方程,求得回归系数的最小二乘估计,来验证此模型的科学性。
1 分布函数的拟合检验
若提出假设的形式为 :
H0:F(x)=F0(x),H1:F(x)≠F0(x)(2)
其中F(x)为需要检验的分布函数,F0(x)为已知分布函数,分布函数中可以含有或不含未知参数。假设检验问题称为对分布函数的拟合检验。
常用的假设检验方法有![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586940062310864878742.jpg) 检验和柯尔莫戈罗夫K检验。本文以
检验和柯尔莫戈罗夫K检验。本文以![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586941073310866656252.jpg) 检验为例来进行验证。
检验为例来进行验证。
设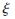 是分布函数F(x)的总体,
是分布函数F(x)的总体,![I_J0GYPEK75I]A@4OQ[2UUL.png I_J0GYPEK75I]A@4OQ[2UUL.png](http://files.chinaaet.com/images/2015/08/22/6357586945341510868071594.png) 是一个样本。将R1=(-∞,+∞)分为m个子区间(xi-1,xi],其中-∞=x0<x1<…<xm=+∞。令vi表示样本
是一个样本。将R1=(-∞,+∞)分为m个子区间(xi-1,xi],其中-∞=x0<x1<…<xm=+∞。令vi表示样本![I_J0GYPEK75I]A@4OQ[2UUL.png I_J0GYPEK75I]A@4OQ[2UUL.png](http://files.chinaaet.com/images/2015/08/22/6357586947396510864353559.png) 落入区间(xi-1,xi]的个数或频数,npi称为样本
落入区间(xi-1,xi]的个数或频数,npi称为样本![I_J0GYPEK75I]A@4OQ[2UUL.png I_J0GYPEK75I]A@4OQ[2UUL.png](http://files.chinaaet.com/images/2015/08/22/6357586948886710865184536.png) 落入区间(xi-1,xi]的理论频数。作统计量:
落入区间(xi-1,xi]的理论频数。作统计量:
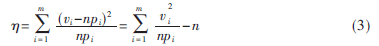
?浊依赖于n和m,以下假定m是定值。
定理1[10](Pearson):如果H0正确,则:

其中:
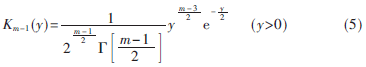
式(5)是![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586970691910865356989.jpg) (m-1)分布的密度函数,这里设F0(x)不含未知数。
(m-1)分布的密度函数,这里设F0(x)不含未知数。
对于定理1, 当n足够大时可认为 。对已知的显著性水平
。对已知的显著性水平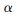 ,从
,从![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586974201610866513742.jpg) 分布表中查得
分布表中查得 (m-1),使得
(m-1),使得 ,即取否定域为(
,即取否定域为( (m-1),+∞)。若
(m-1),+∞)。若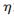 >
> (m-1),则否定H0。
(m-1),则否定H0。
理想置乱情况下,令F0(x)=f(x),F(x)为置乱图像实际的差分直方图分布个数。因为图像差分值取值范围为-255~255,因此将R1=(-∞,+∞)分为510个子区间,子区间长度为1。F(xi)代表差分值为xi的元素数目,即为样本落入子区间(xi-1,xi]的频数,因此有样本频数vi=F(xi)。理论频数npi=F0(xi)=f(xi)。根据式(3)构造![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586991491510862967085.jpg) 检验指标:
检验指标:

由于n足够大,因此,可认为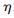 ~
~![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586995783010866610139.jpg) (509)。自由度为509,取值较大,因此
(509)。自由度为509,取值较大,因此![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357586997735410862009442.jpg) 分布近似服从N(509,2 * 509),可采用正态分布来进行实际计算。给定显著性水平
分布近似服从N(509,2 * 509),可采用正态分布来进行实际计算。给定显著性水平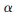 =0.05。
=0.05。
综上所述,当设计的![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587010385510864931474.jpg) 统计指标
统计指标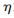 >562.593时,拒绝H0,否则接受H0。
>562.593时,拒绝H0,否则接受H0。
2 线性回归模型的建立
根据置乱图像的差分直方图分布图,分析可能对分布个数产生影响的因素只有差分值。因此建立线性模型:
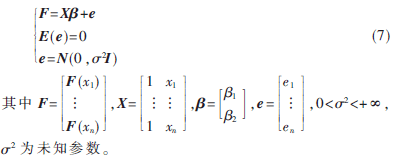
F由差分直方图分布个数的n次观察值构成,F(xi)代表差分值为xi的元素数目。X称为设计矩阵,由常数项和差分值的n次观察值构成,n=511。?茁是未知参数,称为回归系数。e为随机向量,有时称为误差随机向量。
根据线性模型(7),要选择合适的![(FA0CZ]`XME$Z[{P30ZPVV3.jpg (FA0CZ]`XME$Z[{P30ZPVV3.jpg](http://files.chinaaet.com/images/2015/08/22/6357587021464710864069406.jpg) 使误差项的平方和最小,即求
使误差项的平方和最小,即求![(FA0CZ]`XME$Z[{P30ZPVV3.jpg (FA0CZ]`XME$Z[{P30ZPVV3.jpg](http://files.chinaaet.com/images/2015/08/22/6357587022229010867841321.jpg) 的最小二乘估计
的最小二乘估计![KW]SG5L0FX0_UHZ5HHPZ$5E.jpg KW]SG5L0FX0_UHZ5HHPZ$5E.jpg](http://files.chinaaet.com/images/2015/08/22/6357587023524410862108034.jpg) 。
。
若![KW]SG5L0FX0_UHZ5HHPZ$5E.jpg KW]SG5L0FX0_UHZ5HHPZ$5E.jpg](http://files.chinaaet.com/images/2015/08/22/6357587024828810866346563.jpg) 满足条件:
满足条件:
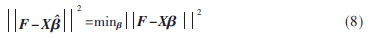
则![KW]SG5L0FX0_UHZ5HHPZ$5E.jpg KW]SG5L0FX0_UHZ5HHPZ$5E.jpg](http://files.chinaaet.com/images/2015/08/22/6357587025800910868938638.jpg) 为
为![(FA0CZ]`XME$Z[{P30ZPVV3.jpg (FA0CZ]`XME$Z[{P30ZPVV3.jpg](http://files.chinaaet.com/images/2015/08/22/6357587026896210869655179.jpg) 的最小二乘估计。令:
的最小二乘估计。令:
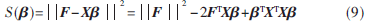
将式(9)对![(FA0CZ]`XME$Z[{P30ZPVV3.jpg (FA0CZ]`XME$Z[{P30ZPVV3.jpg](http://files.chinaaet.com/images/2015/08/22/6357587028548010869552721.jpg) i求偏导并令其等于0,可得到正规方程组:
i求偏导并令其等于0,可得到正规方程组:

因为X的秩rank(X)=2,因此最小二乘解唯一,并由下式给出:

?滓2的无偏估计为:
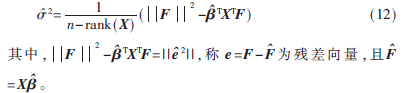
对每一幅图像,其平均残差为:

3 实验结果
3.1 分布函数拟合检验
利用文献[5]中的方法对图像进行置乱变换,置乱次数为100次。选取该方法是因为该方法同时实现了像素值和像素位置置乱,具有代表性。对100幅置乱图像进行差分直方图分布特性的假设检验,检验结果如表1所示。


表1中指出,在100幅置乱图像中,差分直方图符合分布模型f(x)的图像数量为56幅,不符合该分布的图像数量为44幅。在符合该分布模型的56幅图像中,最小的?字2指标?浊=454.38,对应的置乱次数T=91。考察该置乱图像和差分直方图(图1)可知,置乱图像具有良好的类似噪声特性,其差分直方图具有明显的线性分布特性。同时可认为该56幅图像已近似达到理想置乱。对于被拒绝的图像,由于其差分直方图分布不符合线性分布,导致![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587031441710869046399.jpg) 指标很大。
指标很大。
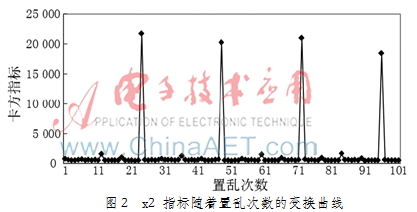
图2给出了?字2指标随着置乱次数的变换曲线。从图中可看出,大部分图像的![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587032562110866219897.jpg) 指标数值分布在1 000以下。但是当T=24、48、72、96时,该统计指标远远高于其他值。考察具有上述置乱次数的图像及其差分直方图,这些图像有着明显的规则性,且差分直方图分布与线性模型相差很大,与参考文献[1]中的置乱度评价结果完全吻合,这说明本文设计的
指标数值分布在1 000以下。但是当T=24、48、72、96时,该统计指标远远高于其他值。考察具有上述置乱次数的图像及其差分直方图,这些图像有着明显的规则性,且差分直方图分布与线性模型相差很大,与参考文献[1]中的置乱度评价结果完全吻合,这说明本文设计的![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587033723610868633665.jpg) 指标能够科学、合理地反映样本频数与理论频数间的差别。
指标能够科学、合理地反映样本频数与理论频数间的差别。

图3给出了不同的![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587035365310867559391.jpg) 指标下所求的p值分布。概率p<0.05的图像均认为其差分直方图分布与模型f(x)不相符。由于p具有如下性质:(1)0≤p≤1;(2)理想置乱时,p=1。因此该p值可作为图像置乱度评价参数直接进行置乱度评价,比如当
指标下所求的p值分布。概率p<0.05的图像均认为其差分直方图分布与模型f(x)不相符。由于p具有如下性质:(1)0≤p≤1;(2)理想置乱时,p=1。因此该p值可作为图像置乱度评价参数直接进行置乱度评价,比如当 =454.38时,可认为具有最好的置乱效果,对应p=0.96。
=454.38时,可认为具有最好的置乱效果,对应p=0.96。
3.2 回归方程系数预测
进行分布函数拟合检验的目的是选择出置乱效果较好的图像,剔除不理想的测试样本。对于接受H0的56幅图像,首先计算其差分直方图,然后进一步根据式(11)对差分直方图分布函数的系数进行最小二乘估计。图4、图5给出了56幅置乱图像差分直方图分布函数的回归方程系数最小二乘估计值的分布图。
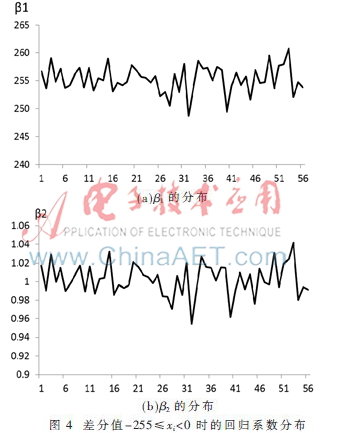
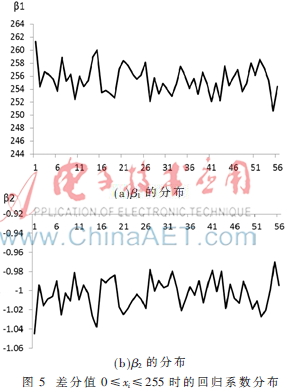
由回归系数分布图4和图5可以得出:(1)常数项系数β1大部分在区间[250,260]范围内取值,与差分值取值范围无关。(2)系数β2的取值和差分值取值范围有关,当差分值-255≤xi<0时,β2∈[0.9,1.1];当差分值0≤xi≤255时,β2∈[-1.1,-0.9]。
根据图4和图5,为了消除样本独立性对系数的影响,求出线性模型最终的系数,进一步计算β1、β2的均值(表2),可知式(7)与所提出的线性模型(1)完全吻合,验证了理想置乱图像差分直方图线性模型(1)的正确性。

3.3 残差分析

在回归分析过程中假设误差e服从均值为0的正态分布(式(7))。图6给出了56幅图像的平均残差分布图,平均残差根据式(13)进行计算。由图可知,大多数图的平均残差都接近于0,说明误差的统计分布符合式(7)对误差e的统计分布特征的假设。
4 总结与展望
由于前期研究中提出的理想置乱情况下图像差分直方图分布模型没有进行严格的数学证明,缺乏理论基础。为了解决该问题,本文立足于统计分析,利用线性![(J]MVU0Z3SQH3(M08PPB73G.jpg (J]MVU0Z3SQH3(M08PPB73G.jpg](http://files.chinaaet.com/images/2015/08/22/6357587047988910866497049.jpg) 假设检验及回归模型预测理论,通过将实际置乱图像的差分直方图分布和参考文献[1]中提出的线性模型进行分布函数拟合检验,选出置乱效果好的置乱图像,进一步对这些进行回归系数预测。实验结果验证了在理想置乱情况下,置乱图像的差分直方图服从线性分布,实验结果与参考文献[1]吻合,为理想置乱图像差分直方图模型的提出提供了理论基础。
假设检验及回归模型预测理论,通过将实际置乱图像的差分直方图分布和参考文献[1]中提出的线性模型进行分布函数拟合检验,选出置乱效果好的置乱图像,进一步对这些进行回归系数预测。实验结果验证了在理想置乱情况下,置乱图像的差分直方图服从线性分布,实验结果与参考文献[1]吻合,为理想置乱图像差分直方图模型的提出提供了理论基础。
在以后的研究工作中,重点应研究以自然图像和理想置乱图像统计特征为基础的评价模型库的建立,来解决缺乏统一评价标准的问题,完善置乱度的盲评价指标体系。相应的置乱度评价体系的发展也能对图像置乱算法的研究起到重要的指导作用。
参考文献
[1] LIU L,ZHANG Q,WEI X.A RGB image encryption algo-rithm based on DNA encoding and chaos map[J].Computers& Electrical Engineering,2012,38(5):1240-1248.
[2] EI-LATIF A A A,NIU X,WANG N.Chaotic image encryp-tion using bezier curve in DCT domain scrambling[C].Commun.Comput.Inform.Sci,2011:30-41.
[3] 吴成茂,田小平.三维不等长Arnold变换及其在图像置乱中的应用[J].计算机辅助设计与图形学学报,2010,22(10):1831-1840.
[4] 凌大旺,禹思敏.基于嵌入式系统的混沌数字图像加密研究[J].电子技术应用,2012,38(3):20-22.
[5] 张统权,何建农.基于混沌细胞自动机的图像加密算法[J].微型机与应用,2013,32(22):44-47.
[6] 王新新,布挺.基于图像表面积的置乱程度评价算法[J].安徽大学学报:自然科学版,2011,35(4):48-52.
[7] 刘家胜,朱灿焰,汪一鸣,等.基于位置相关性的图像置乱效果评价方法[J].计算机工程,2010,36(24):208-210.
[8] ZHAO L,ADHIKARI A,KOUICHI S.A new scrambling evaluation scheme based on spatial distribution entropy and centroid difference of bit-plane[Z].2011:29-44.
[9] 王聪丽,陈志斌,薛明晰,等.基于图像差分统计特性的图像置乱度盲评价线性模型[J].计算机应用,2012,32(12):3470-3473.
[10] 叶其孝,沈永欢.实用数学手册(第2版)[M].北京:科学出版社,2006.

