摘 要： 在图像获取过程中，存在很多造成图像退化的因素，因此需要对图像进行复原。本文对现有的典型复原方法进行了综合分析。介绍了图像一般退化模型和运动模糊退化模型的建立方法；对退化模型的点扩散函数的估计方法进行了分析；对当前的一些复原算法进行了总结。对图像复原技术未来的发展方向进行了预测。
0 引言
在获取图像的时候，由于相机聚焦不佳，相机和物体在曝光的短暂时间内存在相对的移动，或者受传感器的噪声、大气湍流、粉尘以及光线明暗变化等影响，都会造成图像的退化，导致图像模糊。为了从模糊的图像中提取有用的信息，图像复原成为了图像处理中的重要研究方向和数字图像处理的一个重要应用[1]。图像复原是将退化的图像进行处理，通过一些复原算法改进图像质量，尽可能地复原图像的本来面目。目前运动模糊是造成图像退化的主要原因，是图像复原中较难处理的一类情况，也是目前研究的热点之一[2]。对于运动模糊图像的复原一般是通过建立运动模糊图像模型得知图像退化的原因，针对具体的原因采取相应的复原算法得到清晰的图像。在模型的建立中点扩散函数（PSF）的确立是最关键的，目前对于PSF的确立存在很多方法。
1 运动模糊图像退化模型的建立
图像复原是建立在图像退化模型基础上的,因此对于模型的建立尤为重要。图像退化原因的多样性导致退化模型的建立比较复杂[3]。根据图像退化的性质一般可以分为两类退化来建立退化模型。
1.1 图像一般退化模型的建立
有噪声的情况下，图像退化/复原模型的描述如图1所示[2,4-8]。
图中f(x, y)为原始图像，h(x, y)为退化函数即点扩散函数（PSF），n(x, y)为噪声项，g(x, y)为退化后图像。图1所示退化模型的数学表达式为[4]：
把上式空间域形式转化为频域形式为：
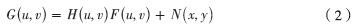
其中， G(u,v)、F(u,v)、H(u,v)、N(u,v)分别是g(x, y)、f(x, y)、h(x, y)、n(x, y)的傅里叶变换。
1.2 运动模糊图像退化模型的建立
图像获取中，景物与相机发生相对运动，造成图像的运动模糊。由于曝光时间短，认为曝光时间内景物的运动是匀速运动，因而匀速直线运动模糊图像的恢复是现在图像复原研究的主要方向之一。匀速直线运动模糊退化模型的建立方法如下[6,9]：
令图像f(x, y)为一个平面运动图像，其中在x和y方向上运动分量分别为x0(t)和y0(t)，采集时间长度为T，在有噪声的情况下，运动模糊图像g(x, y)为：
图像运动模糊常有一定角度，为了方便起见，一般将图像旋转到水平方向上。如图2所示，图像与竖直方向具有一定的角度Φ，为了方便处理需要把图像顺时针旋转Φ进而处理图像。
令b为物体运动的距离，T为曝光时间，即:
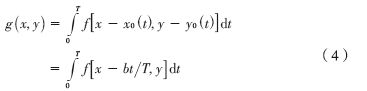
对上式进行离散化：
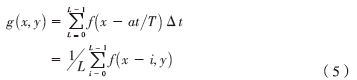
其中，L为像素数，Δt为像素的拖延时间。一幅模糊图像由多个原图拖延叠加而成。通过离散化式（5）和图像一般的退化模型的表达式（1）的对比可以得出[6]：
式（7）是水平模糊方向的退化模型，h(x, y)即为点扩散函数PSF，G(u, v)、F(u, v)、H(u, v)分别是g(x, y)、f(x, y)、h(x, y)的傅里叶变换，N为图像的宽度。
2 PSF的确定
由图像的复原公式得知，建立图像退化模型的关键是确定点扩散函数（PSF）。通过点扩散函数可把图像复原分为两种形式[1,10-12]：
第一种是点扩散函数已知的情况下对图像进行复原，对于匀速直线运动造成的模糊，PSF为[8]：
其中d是模糊长度，θ为模糊角度。把上式的PSF代入图像复原公式就可对图像进行复原，得到清晰的图像。
第二种是点扩散函数未知的情况下，通过估计的方法确定点扩散函数。其方法包括图像观察估计法、模型估计法、实验估计法[1]、频谱特征估计法、依据摄像机参数指标估计法等。
3 图像复原算法
退化模型建立后，可采取相应的处理算法对图像进行复原。复原算法根据性质的不同可分为：基于迭代思想的复原算法、基于非迭代思想的复原算法以及一些新兴的复原算法。
3.1 基于非迭代思想的图像复原算法
3.1.1逆滤波复原算法
逆滤波法通过模糊图像的傅里叶变换来估计原图的傅里叶变换。模糊退化模型的傅里叶变换方式为：
通过上式对图像进行复原的公式为：
再对F(x, y)进行傅里叶反变换就是复原图像f(x, y)。
对于逆滤波算法来说，由于图像的复原公式为一个分式，所以如果H(x, y)很小，则图像F(x, y)就会很大，这相当于扩大了噪声，使图像的复原效果明显变差，但是对于无噪声的图像复原效果则很好。
3.1.2维纳滤波复原算法
算法复原宗旨是使原始图像与恢复图像之间的均方差最小[13]。其基本的原理是寻找一个使如下统计误差函数最小的估计图像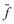
：
其中E是期望值操作符，f是未退化的图像，该表达式在频域可表示为 [14]：
其中，H(u,v)表示退化函数，
表示H(u,v)的复共轭，
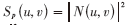表示噪声的功率谱，
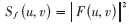表示为退化图像的功率谱。
此算法克服了极点干扰的问题，而且向量和标量均适用[15]。但这个算法在信噪比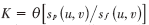
的确定上存在着计算复杂的问题。其未退化图像和噪声的功率谱必须已知，而且需要已知系统的点扩散函数。可以从噪声的功率谱以及退化图像的功率谱上入手精确地解决信噪比，以提高维纳滤波算法的复原效果。
3.1.3 最小二乘复原算法
最小二乘法分为有约束条件和无约束条件两种。无约束条件的最小二乘法是使退化过程中对原图的线性估计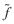
在最小二乘意义下接近模糊图像。
有约束的最小二乘法通过预先设定的约束条件（
,μ为噪声项），使得图像f的像素值接近响应图像g中相应像素值，然后把迭代函数代入复原公式求得复原图像。此算法存在着最优解不稳定的问题。现在有学者采用空间迭代的方法求得问题的解[16]。最小二乘复原算法处理由高噪声和中等噪声造成的图像模糊效果最佳。
维纳滤波是建立在最小化统计准则基础上，所以在平均意义上是最优的，而本算法对于每一幅图像都会产生最优的效果[1]。
3.2 基于迭代思想的图像复原算法
3.2.1 最大熵算法
最大熵算法是使用最大熵约束条件对图像进行恢复。其基本思想是使复原图像的熵与噪声图像的熵相加值最大[17]。令图像函数有正值，则一幅图像总的能量为：
图像的熵为：
噪声熵为：
使Hf + Hn的值最大，然后进行图像复原。
这种算法可有效抑制噪声，而且可以有效地对图像的缺失部分进行恢复。由于该算法为非线性算法，数值的计算比较麻烦，通常以迭代的方式进行计算，耗时且计算量大。因此对于最大熵复原算法的改进可以从解决计算量的方式上入手，找到一种快速的计算方法得到相应的数值，提高算法的效率。
3.2.2 L-R算法
Lucy-Richardson算法是在像素点满足泊松分布的情况下，在贝叶斯条件概率模型的基础上采用极大似然估计通过迭代的方法求解清晰的图像[7,18]。
这种算法在信噪比比较低的情况下，图像的复原可能会出现斑点，而且算法的迭代对图像噪声有放大的功能[15]，所以本算法只适用于无噪声的情况，通过迭代次数的增加使图像第k+1次迭代效果即f(x,y)k+1收敛于原清晰图像f(x,y)，则迭代停止。所以如何克服噪声的干扰是本算法改进的关键所在。
3.3 新兴的图像复原算法
3.3.1 神经网络图像复原算法
伴随着神经网络研究的发展，神经网络在图像复原处理中也得到了应用。基于神经网络的图像复原方法大体可以分为两类：
第一类是基于Hopfield神经网络的图像复原，将图像复原问题转化为极小值的问题来处理，再映射为Hopfield的能量函数，从而利用Hopfield网络求解最优问题[19]。
第二类是运用大量的原图与模糊图像进行学习训练，再利用训练后的网络进行图像复原[16]。
神经网络算法能够通过输入数据自适应找到隐含在样本中的内在规律，使其具有很高的推广能力，但是算法的实施关键在于怎么处理数据与网络函数的映射。
3.3.2 图像超分辨率复原技术
这种复原技术是指利用多帧低分辨率图像，求解成像的逆过程，重建原图的高分辨率图像。超分辨率重建过程可分为三步：（1）预处理，即去噪；（2）配准，即对低分辨率序列间的矢量进行估计；（3）重建，即把多帧低分辨率信息融合在一起。这种技术能够在不改变成像设备硬件的前提下实现优于系统分辨率的观测，最早由Harris和Goodman于上世纪60年代提出。后来学者们又提出了长椭球波函数法、线性外推法和叠加正弦模板等方法。80年代末提出了能量连续降减法、Bayesian分析法和凸集投影等方法。
4 图像复原技术的总结与展望
图像复原问题特别是运动模糊图像复原问题成为了当今图像技术研究的热点。目前的算法都存在弊端，如逆滤波由于无法摆脱噪声的干扰而只适用于无噪声或者噪声比较小的情况；维纳滤波复原算法对噪声有很好的抑制但却很难计算信噪比；最小二乘法对于处理受到高噪声和中等噪声影响造成的模糊图像效果最佳。
另外基于迭代思想的方法中，最大熵算法不用对图像事先做太多的假设，可以有效地抑制噪声和对图像的细节进行较好的恢复，提高了分辨率，而且可以有效地对图像的缺失部分进行恢复,但却存在着数值计算麻烦的问题。Lucy-Richardson算法采用迭代的方法进行图像复原，但有噪声干扰的情况下，此算法的迭代对图像噪声有放大的功能。所以如何克服噪声的干扰是改进本算法的关键。
图像复原问题的未来研究方向将主要围绕参数识别和复原滤波两方面展开，参数识别问题以后会向着增加先验知识的方向发展，而复原滤波算法的研究未来会以去除噪声与图像恢复相结合做为研究的重点，做到在图像复原的过程中不引入任何的噪声。这是对传统复原算法改进的方向。还有一种发展方向就是开发新的复原算法，特别是神经算法的出现为图像复原提供了新的研究思路，也为以后的研究打开了新的方向。另外传统的图像复原技术能够分析模糊的原因，但是只能将频率复原到衍射极限相应的截止频率处，而截止频率外的信息将丢失。现在的超分辨率复原方法却能恢复丢失的信息，这将是未来图像复原研究的另一重要方向。
参考文献
[1] 曾晶. 运动模糊图像复原的探究[J]. 佳木斯教育学院学报, 2012（10）：451,455.
[2] 王若琳, 程耀瑜. 基于 Radon 变换的运动模糊图像复原研究[J]. 电子测试, 2013 (1): 4-7.
[3] BEN E M, NAYAR S. Motion-based motion deblur-ring[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2004, 26(6):689-698.
[4] 程姝, 赵志刚，吕慧显，等. 顺序结构的运动模糊图像复原技术综述[J]. 计算机应用, 2013, 33(A01): 161-165.
[5] 王敏, 田启川. 改进的运动模糊图像复原算法[J]. 微型机与应用, 2011, 30(6): 37-40.
[6] 王秋云, 王轶群. 基于Lucy-Richardson算法的运动模糊图像复原研究[J]. 自动化仪器仪表，2013（2）：18-19,22.
[7] 孟凡菲. 基于盲解卷积算法的运动模糊图像复原[J]. 科技信息, 2012 (32): 128-128.
[8] 闫永存, 杨燕翔, 黄小莉, 等. 匀速直线运动模糊图像复原的改进算法[J]. 电子设计工程, 2012, 20(3): 145-148.
[9] 高治雄, 金韬.一种高鲁棒性的运动模糊图像复原算法[J]. 华东理工大学学报: 自然科学版, 2012, 38(4): 506-510.
[10] Rafael C G,Richard E W. 数字图像处理(第二版)[M].阮秋琦,阮宇智,等译.北京:电子工业出版社,2007.
[11] MOGHADDAM M E,JAMZAD M.A comprehensive study to findthe effect of different noise removal methods on linear motion blurparameter estimation[C]. IEEE 13th International Conference on Systems Signals and Image Processing，Piscataway: IEEE, 2006.
[12] FERGUS R, SINGH B, HERTZMANN A, et al. Removing camerashake from a single photograph[J]. ACM Transactions on Graphics(TOG)-Proceedings of ACM SIGG RAPH 2006, 2006,25( 3) :783 -794.
[13] 孟庆浩, 周荣彪. 复合帧运动模糊图像复原方法研究[J]. 计算机工程, 2006, 32(13): 187-189.
[14] Gonzalez R C，Woods R E，Eddins S L.Digital Image Processing Using MATLAB[M].北京：电子工业出版社,2005.
[15] 李勇峰. 运动模糊图像复原算法研究[J]. 山西电子技术, 2013 (4): 90-91.
[16] 王芳. 一种新的最小二乘法图像复原算法的研究[J]. 包装工程, 2009, 29(12): 151-153.
[17] 辛玲. 运动模糊图像复原算法综述[J]. 硅谷, 2010 (1): 55-56.
[18] 余恕梅, 檀结庆, 王明珠. 运动模糊图像复原结果中伪像的消除[J]. 计算机工程与应用， 2013, 49(5): 5.
[19] 吴城磊. 连续 Hopfield 神经网络图像复原算法的改进[J]. 电脑知识与技术: 学术交流, 2006 (10): 99-100.
[20] 卓力,王素玉,李晓光.图像/视频的超分辨率复原[M].北京:人民邮电出版社,2011.