摘 要： 排课是学校教学管理中非常重要的工作。排课问题是一个有约束、多目标的优化组合问题，并且已经被证明是一个NP完全问题。高职院校与一般中小学校相比，课程的编排需考虑的因素更多，极为复杂。以广东农工商职业技术学院计算机系实训室排课系统的算法作为研究对象，根据我院的一校多区等实际情况和计算机实训课程的特点进行排课算法的研究，采用多重优先法则与遗传算法相结合的方法有效解决了排课问题，不但排课效率高，而且容易得到优质课表。

　　关键词： 排课；实训室；遗传算法；多重优先

0 引言

　　排课问题就是在给定教师资源、教室资源和开课计划的前提下，如何合理地安排课表问题。其实质是含约束条件的目标函数优化问题，是运筹学中的时间表问题(Timetable Problems，TTPs)[1]。1975 年， Even S 证明了高校排课问题在本质上属于NP完全问题[2]。遗传算法 GA作为随机优化与搜索方法，通过对可行解进行选择、交叉、变异等遗传算法的作用使种群不断进化，最后得到全局最优解或近似最优解，成为求解排课问题的主要方法[3]。

　　近年来，高职院校不断进行扩招，专业、学生、教师不断增加，使得教室、实训室等资源变得紧缺，排课问题变得越来越严峻。由于各个学校的具体情况各不相同，通用的排课软件已不能很好地适应每个学校。本文对我院一校多区等实际情况和计算机实训室课程的特点进行了深入分析，在使用遗传算法的基础上结合多重优先的方法先得到初始种群，然后通过遗传算法的选择、交叉、变异、迭代进行寻优，最终得到优质课表[4]。相对于其他利用遗传算法解决排课问题的算法，该算法更具针对性，主要体现在对课程的多重优先的分层编排和课程编码设计上。

1 计算机系实训室排课问题分析

　　本学院有约两万名学生，计算机系有学生两千多名，分布在两个校区，一、二年级的学生在北校区、三年级的学生在西校区。教师同时担任两个校区的课程。学院教务处负责安排理论+实践课程的理论学时（在多媒体教室上），计算机系负责安排理实一体化课程和理论+实践课程的实训学时（在本系实训室上），计算机实训室排课是在教务处已排好的理论课课表的基础上进行。本系有30多间实训室，除少数专业实训室（如摄影室、手绘室、网络实训室等），大部分均为普通机房，可承担一般课程的实训教学，普通机房的配置分为高、中、低三级，根据课程的要求最大化地利用好实训资源，提高教学效果。

　　根据本学院的实际情况，实训室排课除了要满足一般课表的要求，还有一些特别要求，应遵循的基本原则有：

　　（1）硬约束条件，即必须满足的条件：

　　①教师不能冲突，同一教师在同一时间不能教授两门课程（课程包括实训课和理论课）；

　　②实训室不能冲突，同一实训室在同一时间不能安排两门课程；

　　③班级不能冲突，同一班级在同一时间不能安排两门课程（课程包括实训课和理论课）；

　　④教师不能在同一个半天在不同校区上课；

　　⑤课程必须安排在符合基本实训要求的实训室上，专业性很强的课程要专门安排专业性实训室，一般课程按内容要求不能低于最低配置的实训室；

　　⑥实训室容量必须满足上课学生人数，现有实训室的容量一般都大于班级人数的编排；

　　⑦全院公共选修课时间段不安排课程。

　　（2）软约束条件，不一定要满足，但满足能得到较优解：

　　①同一门课程在一周之内应间隔排列。如某课程周学时为4学时，以2学时为一个教学单位，需安排两次，两次的安排时间有合理间隔；

　　②同一班级的课程应在一周内分散安排；

　　③课程尽量安排在上课效果好的时间段，晚上和周五的下午尽量不排课；

　　④对于上课时间有特殊要求的教师和课程尽量满足其时间要求。

　　在以上列出的软硬约束中，硬约束必须要满足，而软约束是在满足硬约束的前提下尽量满足。

2 排课遗传算法设计

　　2.1 编码设计

　　使用二维矩阵来表示一个总的课表。横坐标表示时间，纵坐标表示实训室，课程信息包括课程名称、授课教师、班级、实训室要求等信息。排课就可以简化成将课程信息放入这个二维矩阵。采用这种操作，不可能出现同一时间的教室冲突，只要保证在同一时间中教师和班级不冲突，同一半天中教师没有被安排在不同校区就可以得到一份可行课表。具体编码设计如下：

　　（1）二维矩阵的横坐标表示时间片

　　高职院校的课程一般两节课连上，两节课为一次课，上午两次课，下午两次课，因课程较多，有时晚上也需排课。每次课作为一个时间片来安排课程，每天6个时间片，每周5天，则可分为30个时间片。

　　每个时间片表示为Tij, i∈{1,2,3,4,5}，j∈{1,2,3,4,5,6}，i表示星期几，j表示一天内的哪一个时间片。具体如表1所示。

　　（2）二维矩阵的纵坐标表示实训室

　　实训室代码设置为4位，R=（R1 R2 R3 R4），其中：R1表示实训室所在校区：1表示北校区，2表示本部；R2表示实训室的配置类型：1表示高配置，2表示中配置，3表示低配置，4表示摄影室，5表示手绘室，6表示网络实训室；R3表示实训室可容纳的学生数；R4表示各类型实训室的编号。

　　（3）课程信息代码

　　课程信息代码设置为10位，C=（C1 C2 C3 C4 C5 C6 C7 C8 C9 C10），其中：C1表示实训室所在校区：1表示北校区；2表示本部；C2表示对实训室的配置类型要求，具体代码表示与R2相同；C3表示班级人数；C4、C5表示班级代码；C6、C7表示教师代码；C8、C9表示课程名称；C10表示课程每周需上的次数。每门课程根据学时确定每周需上课的次数，一般为1~3。

　　2.2 初始群体

　　2.2.1 初始群体的产生

　　排课需考虑的约束很多，如果全部直接使用随机生成的方式很难得到有效的无冲突课表，故本文根据实训室排课的特点，有针对性地设计了多重优先和随机生成相结全的方法，生成无冲突课表作为初始基因。

　　初始基因（无冲突课表）的生成分为两大部分：

　　（1）初排

　　先将课表分为北校区课表和西校区课表两部分，分别进行预排。初排时将课室信息采用多重优先和随机的方法将其分层安排到相关的教室，对课室的安排先遵守约束性再随机，使得实训资源的分配达到最大化。安排的时间片均随机。具体如下：

　　①在已排好理论课的课表基础上，将全院选修课的时间片标注出来，该时间段不排课；

　　②将少量的对实训室有特别要求的课程排入指定的实训室，如摄影课排入摄影室，手绘课排入多功能手绘室，时间随机；

　　③将少量人数多的课程安排到能容纳该人数的符合要求的实训室，时间随机。因为只有极少的班级人数比较多，也只有一两个实训室的容量比较大，一般实训室的容量都是60位，一般班级的人数也不超过60，所以一般实训室能容纳大部分的班级；

　　④将对实训室配置要求为高的课程随机排入高配置实训室，时间随机；

　　⑤将对实训室配置要求为中的课程随机排入剩余的高配置实训室后，再随机排入中配置实训室，时间随机；

　　⑥将对实训室配置要求为低的课程随机排入剩余的中配置实训室后，再随机排入低配置实训室，时间随机。

　　在分配时，同一课程优先分配到同一实训室。

　　（2）调整

　　经过预排后，所安排的实训室已能满足课程的需要，而且配置高的实训室利用率比较高，实现了资源的最大化利用。但现阶段的课表有可能会出现教师上课时间冲突、学生上课时间冲突、教师同一个半天被分配到不同校区等问题，所以要进行总体调整。具体操作流程如下：

　　① 将预排好的北校区和西校区课表合并成一个总课表；

　　②在同一时间上检查是否有同一个老师，如果有，则调整到该老师没有上课的其他时间片，实训室不变；

　　③在北校区、西校区同一半天的时间上检查是否有同一个老师，如果有，则调整时间片，实训室不变。

　　④在同一时间上检查是否有同一个班级，如果有，则调整到该班级没有上课的其他时间片，实训室不变。

　　经过调整，得到初始无冲突课表。课表的样式如表2所示。一份课表作为一个基因V。

　　2.2.2 初始群体规模

　　使用同样的方法生成一定数量初始基因构成遗传算法的初始群体。初始群体的规模不宜过大或过小。过大计算量大，收敛慢；过小则不利于得到最优解。这里的初始群体规模设为30，得。

　　2.3 适应度函数

　　初始群体均为无冲突课表，满足了课表的硬约束条件，但对软约束条件的满足是不一样的。为了判断课表的优质程度，得到最优课表，需根据排课的软约束条件构造相应的适应度函数进行评价。初排时已充分考虑实训室优质资源的高效使用，现评价只需考虑课程安排的时间。

　　（1）上课时间效果值计算

　　课程尽量安排在上课效果好的时间。一般上午上课效果优于下午；下午优于晚上；周一、周二优于周四、周五等。设定的每天各个时间段的效果值如表3所示。

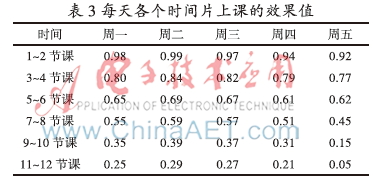
　　整个课程表中占用上课时间的效果值之和为：

　　式（1）中，D表示课程所在时间段的效果值； i表示时间片；j表示课程实训室；r表示实训室总数；missing image file0表示该位置无排课，1表示该位置有排课。

　　（2）课程间隔效果值计算

　　同一门课程一般一周内安排两次，在一周之内应间隔排列，间隔效果值如表4所示。

　　整个课表的课程间隔效果值为：

　　式（2）中，E表示同一课程一周内的间隔时间的效果值，m为课程的门数。

　　（3）适应度函数

　　归总上面约束函数，得出总的适应度函数为：

　　其中，p、q为权值，p=30，q=50。

　　2.4 选择算子

　　为防止已经搜寻到的最优解丢失，让上一次群体中适应度最大的20％的课表直接进入下一代群体中，另外80％的个体使用“轮盘选种”的方法选择进入下一代基因。

　　2.5 交叉

　　因为作为每个基因的课表都是无冲突课程，故在进行交叉和变异时要设计好交叉的方法，不改变课表无冲突的状态。这里以半天的2个时间片的课程安排作为交换单元，因为如果以一个时间片作为交换因子，有可能在半天里将同一位教师分配到不同校区。教务处已排的理论课程、已定的选修课时间、周五晚上的时间单元对应的内容不作交叉，保留原位。

　　2.6 变异

　　在同一时间片里将课程调整到达到最基本配置要求的实训室的空时间片中。因变异的区域限定在同一时间片里，故可以保证课程表的冲突状态。

　　2.7 判断终止条件

　　根据需要进行迭代次数的设置，可随时停止运算。

　　2.8 得出适应度最高的课程表

　　计算出适应度最高的课表作为最终优质课表。

3 各类型课程表的生成

　　由得到的最终优质课表生成各类型的课程表，包括教室安排表、教师安排表、班级安排表。

4 实验

　　使用Visual Studio 2010的C#作为实验程序的编写工具。程序中通过导入外部文件的方式，可随时设置教室、班级、教师、课程、学时安排等约束条件，通过遗传算法的多次迭代得出具有较高适应度的课表。程序运行结果表明，算法的前期收敛速度很快，后期变慢，因为初始基因已为无冲突课表，要得到效率值较优的课表只需较少的迭代次数与时间即可。

5 结论

　　本文针对我院一校多区等实际情况和计算机实训课程的特点，基于遗传算法，使用多重优先的法则先得到无冲突课表作为初始基因，相对于其他使用遗传算法解决排课问题的方法更高效，设计了效果适应度函数、选择、交叉和变异的方法，算法快速收敛，能有效得到优质课表。

参考文献

　　[1] 廖宇力.基于遗传算法的排课问题适应度函数设计[J].现代计算机（专业版），2010(4):53-57.

　　[2] 崔玉连,杨新峰.改进遗传算法在排课问题中的应用研究[J].微型电脑应用,2013，29（10）:48-51.

　　[3] 钟耀广,刘群锋.基于遗传算法的高校排课数学模型[J].东莞理工学院学报,2012，19（5）:4-8.

　　[4] 于干,张军. 遗传算法在自动排课中的应用研究[J].科技向导,2011(30):10-11.