0 引言

    近几年卫星导航系统发展较快，全球已经拥有四个独立的导航系统，统称为全球导航卫星系统（Global Navigation Satellite System，GNSS）。相比早期单一系统，GNSS为用户提供了更多可用卫星和可用信号频点。测量型接收机在作业时需要持续稳定接收卫星信号，早期基于单一系统的测量型接收机会尽量选择开阔、无遮挡的环境进行作业，而GNSS为测量型接收机提供更多卫星、信号频点数量，这使测量型接收机改善了解算精度，同时扩展了使用范围。目前测量型接收机用途十分广泛，如工程测量、工程形变监测和资源勘查等，随着技术的不断提高，其用途也发展到城市道路、建筑工程测量等，所以其作业环境很复杂，有时无法随意选择，这就面临着环境中的电磁干扰问题。

    宽带干扰在作业环境中不常见,多数为人为有意干扰，同时也很难在数字基带部分有效滤除。实际环境中常见的干扰形式为连续波干扰、扫频连续波干扰，白噪声窄带干扰等，是作业中实际面对的电磁干扰类型。本文将这几种干扰类型作为抑制对象，研究滤波算法应用后的影响。

    导航接收机抗干扰的方法较多，如在天线、射频、基带等不同环节实现，时域、空域、频域有不同算法处理等，研究的关注点主要是干扰抑制能力强弱及对导航定位解算精度的影响，而位置解算精度主要是关注对伪距的影响程度。测量型接收机为提高位置精度，主要采用载波观测量、差分解算的方式完成位置计算，如果因抗干扰而加入干扰滤波算法，会对载波观测量精度有何影响，这是目前研究中很少关注的。

    本文通过仿真实验，在数字中频信号中加入固定功率的干扰信号，使用频域干扰抑制技术进行抗干扰处理，分析干扰抑制后信号的相关性变化；建立跟踪模型，跟踪剔除干扰的信号，分析码环、载波环相位测量精度的变化情况。

1 频域干扰抑制技术

    频域干扰抑制思路比较简单，将信号进行频域变换，在频域内分析信号及干扰的幅频特性，使用一定方法对确认为干扰的谱线分量进行抑制，达到消除干扰的目的。频域干扰抑制方法最简单且常用的实现方式为设置检测门限，将超出门限值的谱线分量定为干扰部分并进行处理。卫星导航信号经过长距离传输后到达用户端时衰减很大，信号功率低于环境噪声功率，因此用户接收的主要是白噪声信号，而白噪声的频谱是平坦的，这非常适合于使用门限检测的方式进行频域干扰抑制处理。文献[1]中提出了重叠选择频域干扰抑制方法，并使用此方法对GPS信号进行抗干扰处理，其核心思路如图1所示。

    主要组成部分为：时频域变换（FFT/IFFT）、数据序列加窗、干扰门限生成及干扰抑制、重叠合成结构。

    时频域变换部分主要是将需要处理的卫星数据序列转换到频域，并对频域谱线幅度进行干扰分析及滤除，处理后的数据通过反变换的方式转换到时域供后续处理部分使用。数字时频变换方法主要采用FFT/IFFT实现，设计时重点考虑算法的计算量、资源消耗程度、计算点数几个部分。计算点数选取越多，频谱的分辨率越精确，消耗的资源或计算量越大，因此可根据实际情况合理设计。

    由于FFT计算对数据进行分块处理，相当于乘以矩形窗函数，当信号频率点与FFT的分析频率点不重合时，会引起信号频谱泄露。处理频谱泄露的方法就是使用窗函数对数据进行加权，抑制其旁瓣幅度。不同的窗函数具有不同的旁瓣衰减幅度，同时其主瓣宽度也发生变化，当旁瓣能量降低时，主瓣能量增加，主瓣宽度也将变宽，如果是剔除干扰信号，将有更多的谱线被剔除^[2]。设计时可根据需要抑制的干扰强度合理选择窗函数，平衡主瓣宽度及旁瓣抑制能力的关系。

    加窗可以抑制频谱能量泄露，但因窗函数序列两端平滑减小至零，加权后会造成分块数据在连接处的能量损失，重叠合成处理就为解决这一问题。文献[1]中采用两路50%延迟重叠选择的方法进行信号能量补偿，50%延迟因计算量适中而使用较多，合成结构除重叠选择外也可使用重叠相加的方式，且重叠相加可以获得更小的能量损失^[3]。

    干扰抑制算法采用N-sigma方法^[1]，此方法利用信号的频域幅度的统计值计算干扰抑制门限，计算公式如下：

式中：μ_cale为对数谱线幅度均值；σ_cale为对数谱线幅度标准差；N为自适应调节因子。

    N取值取决于幅度标准差σ_cale的值，按不同情况将标准差划分为预设的四个等级，根据不同等级设计N为不同取值，当干扰功率越强、干扰数量增多时，综合信号的标准差会较大，此时N取值较小，反之当干扰功率较弱时，标准差也会变小，此时N取值较大，确保包含全部有用信号。计算公式如下。

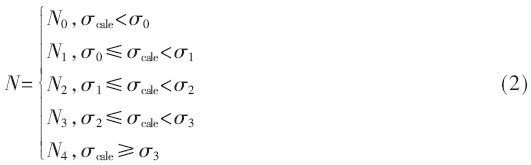
    抑制技术可以选用直接置零或等比例钳位两种方法，直接置零方式将引起较多的信号能量损失，等比例钳位方式虽然可以减少信号能量损失，但也会残留干扰信号能量，相位信息也将受到干扰，会对后期信号误码率产生一定影响。

    本文仿真中设计的频域干扰抑制方法参数如表1。

2 信号相关性仿真

2.1 信号及干扰模型

    卫星导航系统原理上是一个基于码分多址的直接序列扩频通信系统，无噪声的输入信号可表述为：

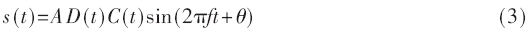
式中：A为信号幅度，D为调制信息码，C为伪随机码，f为载波频率，θ为信号相位。

    数字化的输入信号在移除多普勒值后其序列相关函数如式(4)所示^[4]：

式中：N为序列长度；T_c为伪码码宽；τ为序列时延。

    即序列延时在正负一个码片内的自相关峰为三角函数形式。

    最常见干扰形式为窄带干扰，单音干扰是窄带干扰的一种特殊形式，其模型可表述为：

    通过调整参数A_j1、f_j可改变干扰信号的功率和干扰频点位置。

    窄带干扰可由高斯白噪声通过一个窄带数字滤波器来产生，窄带数字滤波器可用M阶自回归(AR)模型实现。干扰信号表达式为^[5]：

2.2 相关性仿真

    图2所示为频域滤波后信号相关性仿真流程，无噪声信号与干扰信号合成后送入频域干扰抑制模块，经干扰分析抑制后与本地载波混频，分析去除干扰后信号的相关性变化。

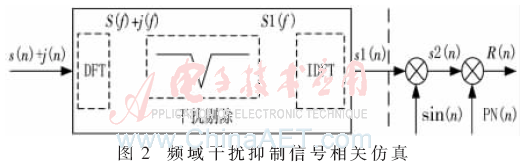
    仿真条件为：输入信号伪码速率10.23 MHz；采样率21 MHz；信噪比-30 dB；干信比50 dB；仿真时间1 ms。

    输入信号为不同中心频点的窄带干扰：窄带截止带宽1.2 MHz(7.3~8.5)，通带带宽1 MHz(7.4~8.4)；窄带截止带宽1.2 MHz(2.0~3.2)，通带带宽1 MHz(2.1~3.10。干扰中心频点在不同位置时相关性与原信号相关性比对如图3所示。

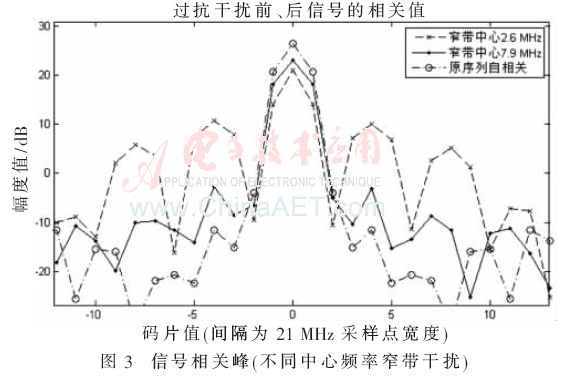
    从图3可以看出，当窄带信号中心频点离信号中心频点近时，相关峰能量损失更多，且曲线的旁瓣上升较大，即信号的低频部分能量较高，且低频部分决定信号单脉宽内的幅度平坦程度；而高频部分能量占比相对减少，高频部分更多影响信号脉宽的边沿陡峭程度。

    图4所示为不同带宽窄带干扰影响比对。窄带通带起点2.1 MHz；过渡带宽度0.1 MHz；带宽取值为0.3 MHz、0.6 MHz、0.9 MHz、1.2 MHz。从图中可以看出，窄带干扰时相关峰损失较大，因窄带干扰频点接近信号中心频点，信号低频谱线损失较多，所以旁瓣较高，其中0.3 MHz带宽时信号能量损失较大，原因是其带宽较窄，加窗后干扰旁瓣能量抑制不理想，而设置的分段加权因子在此条件时较小，导致生成门限较低，将窄带干扰外的一部分有用信号剔除所致。

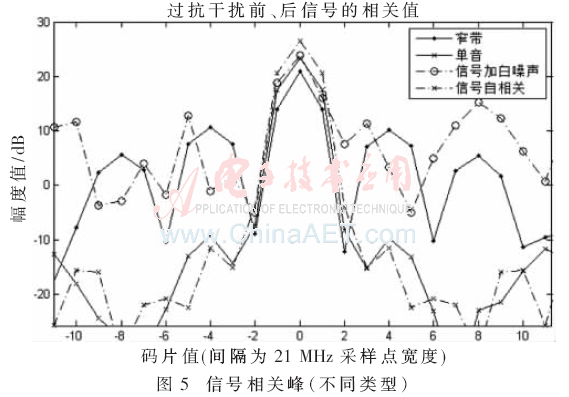
    图5为不同类型信号经过干扰抑制模块后信号相关峰的变化，输入类型为无干扰信号、信号+高斯白噪声、单音信号、窄带信号。在没有干扰及白噪声时，信号的相关峰值最高；当含有白噪声后信号的相关峰值下降，旁瓣能量升高，这主要是受到噪声影响，信号延时超过一个码片后的正交性变差，其主瓣、旁瓣两侧不对称，是因为采样频率稍大于信号频率2倍，采样点相位受噪声影响较大，在一次积分时间内样点的相关曲线会有较大的波动；单音干扰抑制后相关峰值有所下降，但其旁瓣较小；窄带干扰抑制后旁瓣左右对称，旁瓣能量有较大增长，最大旁瓣能量与含白噪声时的旁瓣接近。

3 环路测量精度仿真

3.1 仿真模型

    添加跟踪环路模型，仿真流程变化如图6所示。

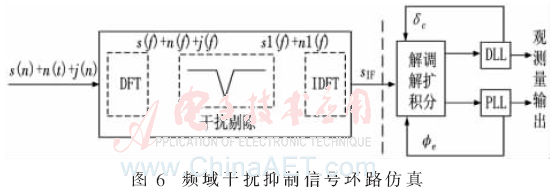
    为进行环路仿真，对仿真模型进行修改，添加噪声项干扰，输入信号模型变化为：s_in(t)=s(t)+n(t)+j(t)，其中n(t)为加性高斯白噪声。

    码环选用二阶非相干超前减滞后延迟锁定环，鉴相器表示^[6]：

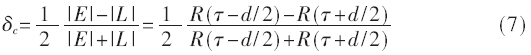
式中|E|、|L|为超前、滞后支路的相干积分幅值；d为超前滞后支路码片间隔。

    噪声带宽与滤波器振荡频率关系式为B_n=ω₀(4ζ²+1)/(8ζ)，ζ为阻尼系数。

    载波环选用三阶科斯塔斯锁相环，鉴相器表示为：

    噪声带宽与滤波器振荡频率关系式B_n=ω₀/1.2。

    稳定跟踪时环路参数选择为：载波环噪声带宽12 Hz；码环噪声带宽0.2 Hz；码环超前滞后间隔1码片；环路积分时间1 ms。

    可使用热噪声估算公式计算环路测量精度大小，载波环热噪声估算公式为^[7]：

式中：载噪比C/N₀值约43 dBHz(信噪比-30 dB、带宽21 MHz)；B_fe为射频带宽取值21 MHz；T_C为伪码序列码片宽度，约97.75 ns。

3.2 仿真结果

    选用不同干扰信号作为输入条件，通过计算测量历元输入信号与本地信号伪码、载波的相位差值，分析码环、载波环的测量精度。

    选取的干扰类型为连续波干扰(CWI)、扫频干扰(SFI)、1 MHz宽度的窄带干扰(NBI)。其中CWI频点2.140 223 MHz；SFI起点2.140 223 MHz，扫频速率40 kHz；NBI起点2.1 MHz，通带带宽1 MHz。

    仿真时间为30 s，测量条件为：信号无干扰无FDIS模块、信号无干扰有FDIS模块、连续波干扰、扫频干扰、窄带干扰5种条件。测量误差统计值如表2。

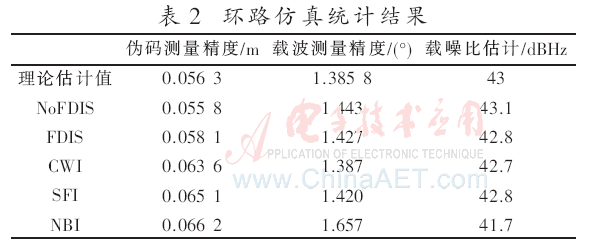
    由统计结果可以看出：(1)伪码、载波测量精度在不同条件时与理论估计结果近似；(2)伪码测量误差随测量条件变化逐渐放大，最差为窄带干扰条件；(3)载波测量误差只有窄带时存在较明显不同；(4)载噪比估计值在窄带干扰时有明显下降，其余干扰条件时存在小幅度下降。

4 结论

    由信号相关性仿真可知，窄带干扰位置不同影响不同，当接近信号中心频点时干扰影响增大；窄带干扰比连续波干扰造成更多的相关功率损失，且旁瓣功率增高。

    由环路仿真结果可知，窄带干扰对伪码、载波的测量精度、载噪比影响最大；伪距测量精度随干扰形式有逐渐变差的趋势；载波测量精度在仿真条件下影响较小。

    在典型的仿真条件下，频域干扰抑制技术可以对设定干信比为50 dB的干扰信号进行抑制，对滤除干扰后的信号进行跟踪，因剔除干扰谱线造成的信号能量损失，会引起测量精度的恶化，但变化程度不大，可以满足1/100相位精度要求，因此干扰抑制算法可以应用于测量型接收机中。

参考文献

[1] CAPOZZA P T，HOLLAND B J，HOPKINSON T M．A single-chip narrow-band frequency domain excisor for a global positioning system(GPS) receiver[J]．IEEE Journal of Solid-State Circuits，2000，35(3)：401-410．

[2] 应启珩，冯一云，窦维蓓．离散时间信号分析和处理[M]．北京：清华大学出版社，2001：104-107，228-235．

[3] 曾祥华.扩频系统频域窄带干扰抑制算法加窗损耗研究[J].电子与信息学报，2004，26(8)：1276-1281.

[4] 张欣．扩频通信数字基带信号处理算法及其VLSI实现[M]．北京：科学出版社，2004：18-20．

[5] 付江志．直扩测控系统中的窄带干扰抑制技术研究[D]．哈尔滨：哈尔滨工程大学，2010.

[6] PARKINSON B W，SPILKER J J．Global positioning system：theory and applications[M]．Washington：USA，American Institue of Aeronautics and Astronautics，1996：361-375．

[7] 谢钢．GPS原理与接收机设计[M]．北京：电子工业出版社，2009：293，317．