摘 要: 设计了一种基于零点优化的低功耗ΣΔ调制器,该结构不需要传统ΣΔ调制器中的数字抵消逻辑部分,可以采用低增益的运算放大器(OTA),减小了设计难度。此外,设计的调制器中积分器的输出摆幅大大减小,积分器的非理想特性得到了抑制。通过优化零点位置,增加了调制器的稳定性和动态范围,信噪比和未进行零点优化相比得到了大大提高。设计的调制器采用0.35 μm CMOS工艺仿真实现,仿真结果表明,在带宽为500 kHz、过采样为16 Mb/s时,信噪比达到90.9 dB, 功耗仅为3.78 mW。
关键词: 低失真;数字抵消逻辑;非理想特性;调制器;信噪比
模数转换器(ADC)作为模拟电路和数字电路的接口,其精度和速度对系统的性能起到了决定性作用。随着通信产品、电脑产品、消费类电子产品的飞速发展,系统对ADC的要求也与越来越高。
在众多ADC中,ΣΔADC能很好地折衷速度和精度,减少了其中模拟部分的精度,得到了广泛的应用[1]。在一些应用中[2],由于采样频率受到了限制,为了达到高精度,不得不使用高阶调制器。但是单环高阶调制器具有潜在的不稳定性,虽然级联结构通过级联多级低阶达到了高阶稳定的效果,得到了广泛的应用。但是级联结构需要数字抵消逻辑模块,来抵消前级产生的量化噪声,以实现高阶整形效果。因此对数字和模拟部分的匹配精度要求很高,为了达到高精度,调制器必须使用高增益,宽带宽,宽摆幅,大摆率的运算放大器OTA,但这样会增加系统的功耗和复杂度。
本文设计了一种基于零点优化的低功耗ΣΔ调制器,该结构对各级量化噪声高阶整形,不再需要传统ΣΔ调制器中的数字逻辑抵消部分,降低了数字模拟部分的匹配要求。此外,本文设计的调制器能减小各级的输出摆幅,提高了稳定性和动态范围。通过优化零点位置,信噪比和未进行零点优化的情况相比得到了很大地提高。
1 基于零点优化的调制器
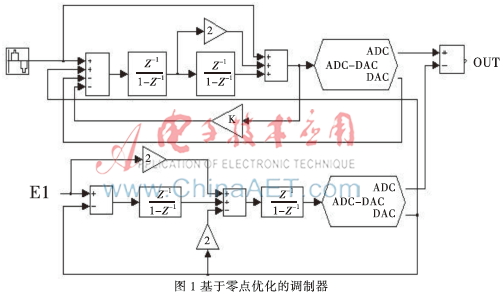
本文设计的基于零点优化的ΣΔ调制器如图1所示。
其传输函数为:
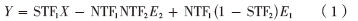
从式(1)可以看出,输出的第一项和第二项与传统级联结构一致,第三项表明E1不止被NTF1整形,还额外乘了(1-STF2)。
理论上,如果使得STF2=1,可以抵消第一级的量化噪声,然而这在实际中难以实现。该结构的关键在于选择第二级的信号传输函数,使得1-STF2能对E1进行整形。对于本文设计的调制器系统:

则

因此输出对E1也进行4阶噪声整形。从式(3)可以看出,和传统的级联结构相比,第二级的量化噪声没有被抵消,而是进行了4阶整形。优点在于该结构不需要传统的数字抵消逻辑部分。因此不存在数字模拟部分失配的问题[3],OTA的设计变得更加简单。缺点在于增加了总的量化噪声,信噪比减小了3 dB。
2 零点优化
本文设计的调制器中,因为第一级积分器处理的信号不是传统级联结构中的E1,使得调制器的动态范围有所减小。通过调整K的值,可以使得NTF的零点分布在带宽内偏移直流处,从而进行零点优化[4]。可以提高系统的动态范围和信噪比。
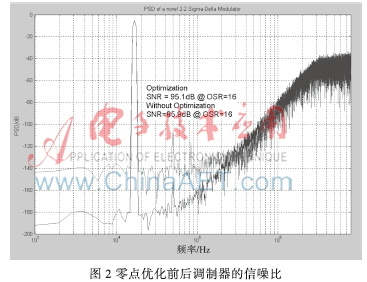
在MATLAB/Simulink下通过行为级仿真,发现在K=0.05时,可以使调制器达到最大的动态范围,信噪比达到95.1 dB(如图2所示),比未经过零点优化提高近10 dB。此外,由于第一级采用了低失真结构,从图 3可以发现除最后一个积分器外,输出摆幅都不到0.5 V。和传统的级联结构相比,积分器的摆幅大大减小,降低了功耗。

3 调制器参数选取及电路设计
采样电容会产生热噪声(又称为KT/C噪声),为了减小热噪声需要采用较大的采样电容。运算放大器的热噪声主要来源于输入差分对和电流源管的沟道热噪声[1]。当Cs=2.4 pF时,
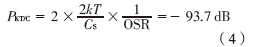
放大器有限增益以及输入寄生电容使采样电容上的差分信号对应的电荷不能完全转移到积分电容,引起积分泄露,考虑运算放大器的有限增益后,一阶积分器传输函数可表示为:

其中,u为OTA增益的倒数,g为所设计积分器的增益。从(5)可以看出,由于运算放大器的增益有限,传输函数的极点发生偏移。增加了带内噪声,带内噪声可表示为关于u的函数。对于单环L阶调制器,加入OTA的有限增益影响后,其带内噪声可表示为:
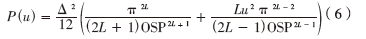
式(6)中第一部分即为量化噪声,第二部分所示为运算放大器的有限增益引入的噪声。本文所采用的结构对第一级和第二级的量化误差均进行4阶噪声整形,所以积分器泄露对它的影响很小,这与4阶单环的影响一致,行为级仿真发现,对于本文设计的结构,当OTA增益大于30 dB时,积分器泄露对调制器的影响很小;而对于传统级联结构,则需要OTA的增益大于70 dB,才能减小积分器泄露的影响(如图4所示)。设计中通常留有一定的裕度,因此本设计中OTA的直流增益定位为40 dB。
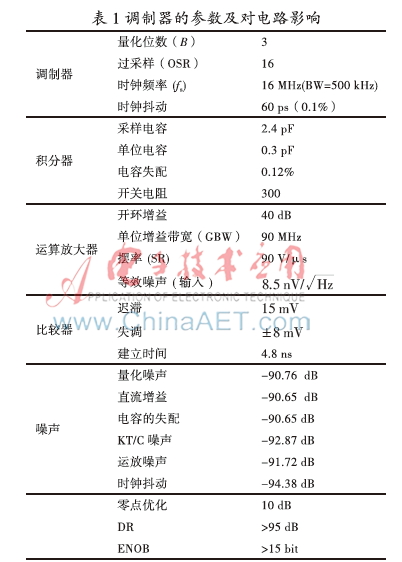
ΣΔ调制器中积分器的建立时间和精度由其中OTA的单位增益带宽和增益决定,为了保证积分器能在半个周期内完全建立,必须在小于半个时钟周期内建立,且精度达到99.9%,据此,本文设计目标定为90 MHz。电路设计中的参数选取和各参数对噪声的影响总结如表1所示。
由于对增益要求不高,为节省功耗采用单级结构,此外,采用增益增强和电流镜来增加增益和带宽,采用AB类输出增大OTA的摆率。本文设计的OTA如图5所示。

其增益为:

从式(7)可以看出,增益提高了1/(1-k)倍,调整k的大小,可以改变其增益。和普通的单级放大器相比,A点的阻抗和寄生电容都增大,因而极点位置降低。为了保证足够的相位裕度,非主极点必须大于3倍GBW,即要求

通过式(8)可以得到OTA能达到的最大增益。由于调制器自身也需要非交叠时钟,开关电容电路不需要消耗额外的静态功耗,因此采用开关电容的共模反馈电路,值得注意的是,共模反馈环路的GBW必须大于主放大器的GBW。因此要求gm5必须大于gm1[5]。
本文折衷了增益和带宽,选取k=0.8,B=9。仿真结果显示OTA的直流增益为42 dB,单位增益带宽为108 MHz(负载为3.1 pF),相位裕度为62°,摆率为121 V/μs,均满足设计要求。在3.3 V电源供电条件下功耗仅为0.75 mW。
在预放大器前,通过一个开关电容网络实现输入信号和第一级两个积分器输出之间相加,由于预放大器一般采用二极管连接的放大结构,输入管栅漏之间电容(Cgd)的存在,使得上一个周期的求和结果会影响到下一个周期,求和结果会出现偏差,需要每个周期对其刷新[7]。本文设计的求和加法器如图6所示,Ck1相求和,Ck2相,预放大器的输入输出短接,对Cgd放电,消除Cgd上存储电荷对求和结果的影响,实现高精度求和。
本文采用的比较器中采用的是一种高速高精度低功耗的动态比较器[6]。在16 MHz时钟下,迟滞小于10 mV,建立时间仅为3 ns,满足行为级仿真要求。
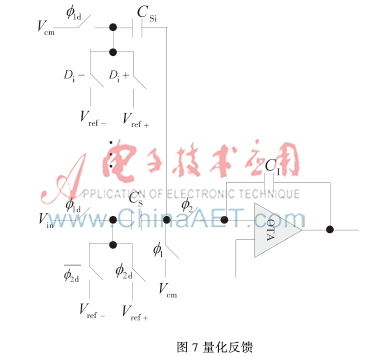
为了避免信号相关性,设计了一种新的量化反馈方式,如图7,2.4 pF的采样电容和8个0.3 pF的单位电容分别处理输入信号和两级量化器的反馈信号。
由于采用了多位量化,为了抑制ADC的非线性,本文采用了DWA技术[8]。
4 仿真结果
本文所设计的调制器采用0.35μm CMOS工艺实现。标准采样频率为16 Mb/s,带宽为500 kHz。过采样率为16 Mb/s。采用Cadence进行多工艺角验证,并且在电源电压在3 V~3.6 V,温度在-40 ℃~75 ℃时调制器能正常工作,信噪比和动态范围均能保持相近水平。当输入正弦信号频率为39 kHz,幅度为-3 dBFS时的输出PSD如图8所示,结果表明,设计的调制器能达到90.9 dB的SNDR(14.8 bit的有效精度)。

本文设计了一种基于零点优化的低功耗ΣΔ调制器,该结构不需要传统ΣΔ调制器中的数字抵消逻辑部分,可以采用低增益的运算放大器(OTA),减小了设计难度。此外,本文设计的调制器中积分器的输出摆幅大大减小,积分器的非理想特性得到了抑制。通过优化零点位置,增加了调制器的稳定性和动态范围,信噪比和未进行零点优化的情况相比得到了很大地提高。电路通过0.35 μm标准CMOS工艺仿真验证,结果表明,调制器最高能达到15 bit的分辨率,功耗为3.78 mW。 结果表明,该结构非常适合应用于宽带宽、高精度、低压低功耗环境。
参考文献
[1] Norsworthy S, Schreier R,Temes G. Delta-Sigma data converters:theory, design, and simulation[M]. NY: IEEE Press, 1996.
[2] Silva J, Moon U, Steensgaard J. et al. Wideband lowdistortion delta-sigma ADC topology[J]. Electronics Letters, 2001,37(12):737-738.
[3] Maghari N, Kwon S, Temes G,C. et al. Sturdy-级联delta-sigma modulator[J]. Electron. Lett., 2006(42):1269-1270.
[4] Schreier R. An empirical study of high-order single-bit delta-sigma modulators[J]. IEEE Transactions on Circuits System II, 1993,40(8):461-466.
[5] Sansen W M C. Aanlog design essentials[M]. Spring Press, 2006.
[6] Yin G M, Eynde F O,Sansen W. A high-speed COMS comparator with 8-bit resolution[J]. IEEE Journal Solid-State Circuits, 1992(27):208-211.
[7] Sandner C, Clara M. A. A 6-bit 1.2-GS/s low-power flash-ADC in 0.13-μm Digital CMOS[J]. IEEE Journal Solid-State Circuits, 2005,40(7):1499-1505.
[8] Baird R T,Fiez T. Linearity enhancement of multibit A/D and D/A converters using data weigthed averaging[J]. IEEE Transaction on Circuits System. II, 1995,42(12):753-762.

