摘 要： 提出了一个全新的混合算法并命名为微粒群差分算法，该算法在标准微粒群算法的基础上结合了差分进化算法用于求解约束的数值和工程优化问题。传统的标准微粒群算法由于其种群单一性容易陷入局部最优值，针对这一缺点利用差分进化算法中的变异、交叉、选择3个算子来更新每次迭代每个粒子新生产的位置以使粒子跳出局部优值。融合了标准微粒群算法和差分进化算法优点的混合算法加速了粒子的收敛速度。为了避免惩罚因子的选择对实验结果的影响，采取了可行规则法来处理约束优化问题。最后将微粒群差分算法用于5个基准函数和两个工程问题，并与其他算法作了比较，试验结果表明，微粒群差分算法算法具有很好的精准性、鲁棒性和有效性。

　　关键词： 混合算法；约束优化问题；微粒群算法；差分进化；可行规则

　　进化算法由于其通用性、可靠性、稳定性、简单性、所需要的信息少等一系列的优点，被广泛地用来解决并且成功地解决了很多约束优化问题。因此，提出了很多基于进化算法的约束处理方法[1-3]。由Kennedy和Eberhart [4] 提出的标准微粒群算法(PSO)便是其中一种应用广泛的仿生算法，它模拟鸟类群体觅食行为来寻求最优解，是一种基于群体智能的随机寻优算法，依赖于个体之间和种群之间的信息共享交换。然而PSO算法由于其种群的单一性容易导致早熟现象，使得优化问题陷入局部最优解。利用其他算法的全局搜索能力来改善PSO算法的缺点，这一混合算法的思想受到很多人的认同，本文正是在此基础上融合了差分进化算法(DE)的进化策略，提出了一种新的PSO、DE混合算法。算法的前半部分同粒子群算法，只是在粒子进行速度、位置更新后，借鉴DE算法的变异、交叉、选择算子以增强粒子群的多样性。

1 背景知识介绍

　　1.1 PSO算法

　　如上所述，PSO是受鸟类觅食行为启发而来的随机全局优化算法。基本PSO的速度和位置更新方程如下：

　　其中，为第i个粒子在第t次迭代时的自身历史最优位置，gbestt是第t次迭代时的种群最优位置。是惯性权重，c1，c2是常量，r1，r2是服从U(0,1)的两个相互独立的随机数。然而这个基本的PSO算法，速度是受到限制的。Clerc和Kennedy[5]引入了收缩因子修改了标准的微粒群模型，速度更新公式变为：

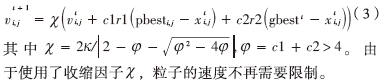
　　1.2 差分进化算法（DE）

　　差分进化算法是由Storn和Price[6]于1995年提出的解决全局优化问题的随机进化算法。算法通过变异、交叉、选择3种操作来领导种群找到最优解。DE算法的主要流程如下：

　　变异操作：本文中采用的是rand/1变异策略即vi=xr1+F×(xr2-xr3)，{xr1, xr2, xr3}， 是在父代种群中随机选择的3个不同个体，并且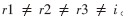。F是一个介于[0,2]间的实型常量因子，称为放缩因子。

　　交叉操作：交叉操作的目的是通过变异个体Vi=(vi,1,vi,2,…,viD)和目标个体Xi=(xi,1,xi,2,…,xiD)各维分量的随机重组以提高种群个体的多样性。算法通过下面的公式产生交叉向量Ui=(ui,1,ui,2,…,uiD)：

　　其中，rand是[0,1]间的随机数；CR是范围在[0,1]间的常数称为交叉变量。

　　选择操作：在贪婪准则的指导下，交叉向量Ui与目标个体Vi竞争。假设待求问题为minf(x),则选择操作可由下式确定：

　　1.3 可行规则

　　本文对于约束的处理采用的是可行规则法，可行规则[7]包含3个方面的内容。

　　⑴任意可行解总是优于不可行解；

　　⑵两个不可行解之间，适应值好的要优于适应值差的；

　　⑶两个不可行解之间，约束冲突值小的要优于约束冲突值大的。

　　总而言之，可行规则法就是找一个离可行域最近的解，即使这个解不在可行域内。

2 微粒群差分算法(CPSODE)

　　2.1 CPSODE算法的原理

　　如上所述，基本PSO算法尽管操作简单但并不是完美的。在本文中，在PSO的基本框架中加入了DE进化策略。基本PSO算法中的粒子在每次迭代中通过学习自身的历史最优位置和全局最优位置来更新自己的速度和位置,从而慢慢靠近优化问题的最优解。换句话说，PSO算法以全局最优位置为中心，吸引所有其他粒子靠近，但是如果最优位置粒子得不到更新，将出现早熟现象。这就是PSO算法陷入局部优值最本质的原因。众所周知，DE算法有着高效的全局搜索能力，其进化策略不仅参数少而且收敛速度快。如果考虑在PSO的位置更新后，对位置矢量进行DE的变异、交叉、选择操作，在这里变异选取了rand/1策略，这样位置矢量就得到更新，使得粒子的运动轨迹偏离既定的轨道，从而全局最优位置得到更新，增强了种群多样性。对DE进化策略的采纳不但加强了算法的搜索能力使算法能够更快的收敛到最优值，而且使算法跳出局部最优值的概率很大，可以有效地避免早熟早收敛。

　　2.2 CPSODE算法的流程

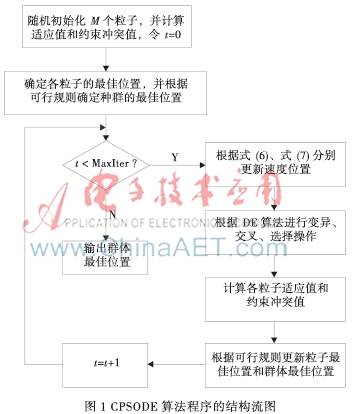
　　为了处理约束，首先在搜索空间随机初始化种群规模为M的粒子群的位置和速度，并计算每个粒子的适应值和约束冲突值，令每个粒子的历史最优位置(记作pbest)为初始化位置，适应值最优的历史最优位置为种群最优位置(记作gbest)；其次根据式⑵、式⑶更新每个粒子的位置和速度，接着对更新的位置进行DE算法的变异、交叉、选择操作，并重新计算各个粒子的适应值和约束冲突值；然后，在可行规则法的指导下，每个粒子更新pbest,并与gbest的适应值进行比较，若较好，则更新gbest，否则保持gbest原始位置。最后循环条件判断，若不满足算法会一次次迭代，直到满足终止条件。程序的结构流图如图1所示。

　　本文对于两处位置更新也做了细节的处理。搜索在搜索范围内才是有效的，因此CPSODE算法为了避免对速度的限制，使用了带收缩因子的速度更新公式即式（3），这样就保证粒子每次迭代的速度都不会致使粒子偏离搜索范围。其次，每次迭代新生产的位置若超出了边界，则超出边界的变量将用如下的法则处理[8]：

　　对每次迭代中DE交叉操作产生的交叉个体Uit，如果交叉个体Uit中任意一维向量Uti,j超出搜索空间，那么将会根据参考文献[9]处理：

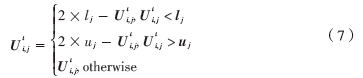
　　2.3 CPSODE算法时间复杂度分析

　　针对约束优化问题，设n为种群的粒子数，d为目标函数的维数，T为最大迭代次数。根据图1所示的CPSODE算法程序结构流程来分析其复杂度。分析结果如表1所示。

　　由上表可以看出，CPSODE算法的复杂度是O(T×n)数量级，n表示任意一个数。

3 实验仿真与分析

　　为了验证CPSODE算法的有效性，证明其相对于其他算法的优点，这一部分用了5 个典型约束测试函数和两个实际的工程问题来验证本文所提出的混合算法，这些测试函数包括非线性和二次函数。

　　3.1 典型约束测试函数优化

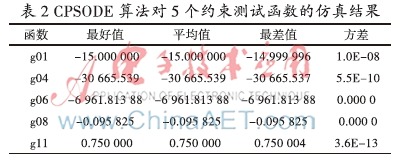
　　对每个测试函数独立运行100次，CPSODE算法参数设置如下：粒子数N=200，F和CR分别为0.4、0.9，g01,g04,g11最大迭代次数设置为500，g04和g08分别设置为300和250。收缩因子missing image file，对函数g11取 ε值为0.000 01。加速常量c1=c2=2.05。表2总结了在以上参数设置下约束测试函数的结果，给出了最好值，平均值，最差值和标准方差。可以看到CPSODE算法均能找到测试函数的全局最优值，而且函数g06、g08能够保持收敛到全局最优值。每个测试函数独立运行100次的标准方差也比较小。

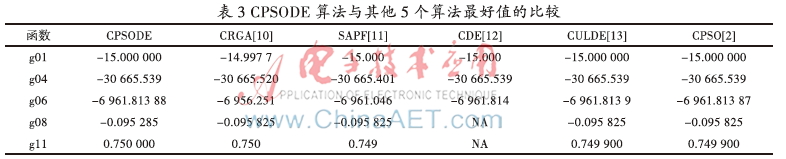
　　CPSODE算法同时也跟CRGA、SAPF、CDE、CLUDE和CPSO算法作了比较。结果如表3、表4、表5所示，NA表示不可求。从表格中可以看出，CPSODE算法要优于CRGA、SAPF、CDE算法，且可与性能很好的CLUDE和ABC算法相比较。就CLUDE算法而言，本文所提出的算法对g11寻找到更好的最好值、平均值和最差值；针对g01函数的平均值和最差值，CPSODE算法结果比其结果要好；对剩下的函数CPSODE、CLUDE算法都可以找到相同的最好值，对g04、g06、g08这3个函数的平均值也相同，最差值方面两种算法对g06、g08的最差值相同，只是对g04函数的最差值，CPSODE要略逊色一些。对于CPSO算法，CPSODE算法对g11函数求得的最好值、平均值、最差值都要优于CPSO算法。总而言之，CPSODE算法具有较好的寻优能力。

　　3.2 工程问题优化

　　为了研究CPSODE算法解决现实生活中工程问题的性能，用两个典型的实际工程问题对算法做了测试，分别是焊接条和伸缩绳问题。每个问题独立运行100次，粒子数N=200，F和CR分别为0.4、0.9，最大迭代次数设置为500。

　　从表6可以看出，CPSODE找到的最优解比参考文献[15]、参考文献[16]结果要好。而且CPSODE算法的平均值比其他算法都好，不仅如此，最差值和方差都是最优的。甚至CPSODE的最差值也要比参考文献[16]最优值好。表明CPSODE对于实际工程问题的求解有其明显的优势。

　　从表7中，可以得出CPSODE算法找到的最优值比参考文献[16]、参考文献[17]结果好，不仅如此，本文所提出算法对伸缩绳问题求解的平均值和方差均优于其他算法，最差值也同样优于除了参考文献[18]之外的其他算法，甚至要比参考文献[17]最优值要好。

　　3.3 CPSODE搜索效率分析

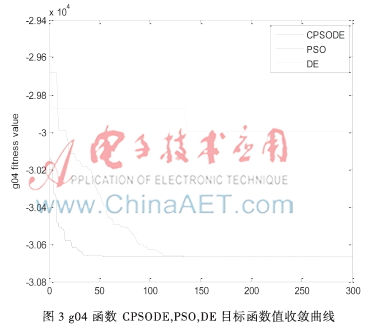
　　图2和图3 分别说明了g01、g04这两个函数收敛到目标函数最优值的迭代过程，从两幅图中可以看出CPSODE比PSO、DE能更快地找到最优适应值。由于混合了DE算法，不仅找到全局最优值而且加快了收敛速度。因此，证实了本文所提出的算法具有良好的全局搜索能力。

　　本文提出了一种新的算法，并命名为CPSODE算法，该算法通过嵌入DE算法提高了单一PSO算法的性能。算法通过局部最优值pbest和全局最优值gbest引导粒子最终收敛到全局最优位置，并在可行规则的指导下[7]来比较粒子更新的位置和其相对应的历史最优位置，然后优胜者更新pbest。在本文的后部分进一步的运用了CPSODE算法对5个典型的约束测试函数和两个典型的约束优化工程问题进行了实验仿真，并对其收敛性和复杂度进行了分析。从比较的研究中可以看出CPSODE展现了其对约束优化问题良好的求解性能。新提出的算法改善了PSO算法的鲁棒性。

参考文献

　　[1] Mohamed A W, Sabry H Z. Constrained optimization based on modified differential evolution algorithm[J].Information Science,2012（194）:171-208.

　　[2] Daneshyari, M, Yen, G.G. Constrained multiple-swarm particle swarm optimization within a cultural framenwork[J].Transactions on Systems,Man and Cybernetics,Part A: Systems and Humans,2012,42(2):475-490.

　　[3] Gandomi A H,Yang Xinshe, Alavi A H. Cuckoo search algorithm: a metaheuristic approach to solve structural optimization problems[J].Engineering with Computers,2013,29(1):17-35.

　　[4] Eberhart R, Kennedy J.A new optimizer using particle swarm theory[C].Sixth International Symposium on Micro machine and Human Science, Nagoya,1995:39-43.

　　[5] Clerc M . Kennedy J. The particle swarm- explosion,stability,and convergence in amultidimensional complex space[J]. IEEE Transactions on Evolutionary Computation ,2002,6(1) :58-73.

　　[6] Rainer S, Kenneth P.Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of global optimization ,1997,11(4) :341-359.

　　[7] Kalyanmoy D.An efficient constraint handling method for genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering ,2000,186(2-4): 311-338.

　　[8] Zielinski K, Laur R. Constrained single-objective optimization using differential evolution [C].IEEE Congress on Evolutionary Computation,Vancouver,BC:IEEE, 2006:223-230.

　　[9] Kukkonen S, Lampinen J. Constrained real-parameter optimization with generalized differential evolution [C].IEEE Congress on Evolutionary Computation, Vancouver, BC:IEEE,2006:207-214.

　　[10] Amirjanov A.The development of a changing range genetic algorithm[J]. Computer Methods in Applied Mechanics and Engineering ,2006,195(19-22):2495-2508.

　　[11] Tessema B,Yen G.G A self-adaptive penalty function based algorithm for constrained optimization[C]. IEEE Congress on Evolutionary Computation,Vancouver, BC:IEEE,2006:246-253.

　　[12] Huang Fuzhuo, Wang Ling, He Qie.An efficient co-evolutionary differential evolution for constrained optimization[J]. Applied Mathematics and Computation, 2007,186(1):340-356.

　　[13] Becerra R L,Carlos A. Coello Coello.Cultured differential evolution for constrained optimization[J].Computer Methods in Applied Mechanics and Engineering, 2006,195(33-36): 4303-4322.

　　[14] Akay B, Karaboga D.Artificial bee colony algorithm for large-scale problems and engineering design optimization[J].Journal of Intelligent Manufacturing, 2012,23(4): 1001-1014.

　　[15] Eskandar H,Sadollah A,Bahreininejad A,et al.Water cycle algorithm-A novel metaheuristic optimization method for solving constrained engineering optimization problems[J].Computer and Structures.,2012（110-111）:151-166.

　　[16] He Qie, Wang Ling.An effective co-evolutionary particle swarm optimization for constrained engineering design problems[J].Engineering Applications of Artificial Intelligence,2007,20(1):89-99.

　　[17] Coello C C, Becerra RL. Efficient evolutionary optimization through the use of a culture algorithm[J]. Engineering Optimizaiton,2004,36(2): 219-236.