0 引言

    以风力发电为代表的可再生能源^[1]具有间歇和随机性的固有属性，随着风力发电渗透率的持续提升，亟需增强当前电网对风电波动性的应对能力。储能电站能够实现能量的存储和释放，成为目前可能解决风电波动问题的重要方式之一^[2]。当前理论研究和示范工程中^[3]，通过配置一定容量比重^[4]的储能平抑其波动性^[5]，可平滑风功率输出。储能电站成为提升大规模风电可调控能力的重要途径^[6]。

    国内外学者指出储能电站目前尚未有特性突出、综合能力显著的储能介质^[7]，优势特性互补的复合储能^[8]是储能技术未来重要的发展方向^[9]。复合储能可弥补单一介质的不足，有利于提升储能电站的适应能力和运行可靠性^[10]，为储能电站基于未来信息构建动态优化控制提供了可能。基于此，本文提出了考虑超短期功率预测的储能电站动态优化控制方法，采用现场风功率运行数据进行了验证分析，结果表明了该方法的有效性和可行性。

1 储能电站充放电策略

1.1 储能介质特性分析

    以铅酸蓄电池和LiB为代表的能量型储能在当前诸多示范工程中获得应用，该类型储能能量密度大，储能时间长，应严格限制其充放电状态转换次数；功率型储能VRB具备频繁充放电切换响应能力，可充放电次数高，适用于呈现频繁快速变化特性的随机分量的波动平抑。

1.2 充放电模型

    考虑到风能分布具有明显的时间周期性，本文选取采样步长为5 min，根据平抑目标确定储能电站所需平抑的功率波动如图1所示。以充放各一次的时长Δt为统计量，可得Δt在采样点区间(1，14]的对应概率和达到85%，为Δt主要聚集区域。由此本文选定两个充放区间作为递进控制步长，得到递进控制步长将以[35，155]min为主要聚集区间。

    根据储能电站介质的运行特性构建主辅两层控制策略，具体充放电模型为：

    (1)VRB优先动作，LiB辅助平抑。递进控制步长内的单次充或放区间能量低于限值E_min，VRB优先动作并在其SOC不越限、充放功率在限值范围的前提下独立平抑波动。核心目标在于发挥VRB的SOC大范围变化特性，严格控制LiB充放电切换次数。该充放电模型对应具体运行模式为：

式中Δt为采样步长。P(t)为平抑目标功率偏移量，P(t)>0对应HESS的充电，其数值对应充电功率；反之对应放电状态，其数值为放点功率。Ei（i=1，2，3，4）为递进控制步长对应的两个充放区间的能量，且E_i=为各充放区间的始末时刻；同理E_i>0则代表HESS吸收能量，反之为释放能量。[E_min-discha，E_min-cha]为VRB优先启动对应的充放能量区间。SOC_VRB(t)为VRB的SOC瞬时值，SOC_max-VRB、SOC_min-VRB分别为VRB的SOC运行上下限值。当满足P_{max-discha-VRB}<P(t)<P_max-cha-VRB时，其中P_max-cha-VRB、P_{max-discha-VRB}分别为VRB的最大充、放电功率，本控制步长内VRB独立完成功率平抑；反之，则LiB辅助启动协调平抑。

    (2)LiB主要动作，VRB辅助平抑。对于非VRB优先动作状况，发挥LiB能量密度高的优势，由其启动并承担主要平抑任务；对于VRB的启动，取决于LiB充放电功率的变化速率及其SOC，其目标在于辅助LiB平抑目标或调整自身SOC以处于较优运行状态。VRB辅助启动条件为：

式中，SOC_max-LiB、SOC_min-LiB分别为LiB的SOC运行上下限值，文中分别取0.9和0.2；P_max-cha-LiB、P_{max-discha-LiB}分别为LiB的最大充、放电功率；ΔP(t)为充放电功率的变化率，且ΔP(t)=P(t)-P(t-1)；ΔP_max-cha-LiB、ΔP_{max-discha-LiB}分别为LiB的最大充放电功率变化率；SOC_LiB(t)为LiB的SOC瞬时值。当LiB、Uc同时启动时，当各自SOC或充放电功率同步越限时，将分别出现弃风和平抑功率不足的状况。

2 储能电站动态优化控制模型

2.1 目标函数

    基于上述充放模型，构建以储能电站SOC运行状态最优为目标的优化控制模型。已知递进控制步长区间的各介质初始SOC_int-LiB、SOC_int-Uc，基于充放电策略，使得本区间内各介质偏移最佳SOC的方差和最小，目标函数如式（3）所示。

    该目标函数主要解决本递进控制步长区间内充放能量在各介质间的协调分配问题。其中，SOC_OLiB、SOC_OVRB分别为最佳运行SOC，本文分别取0.6和0.5；SOC_LiB(t)、SOC_VRB(t)分别为本区间各介质的实时SOC数值，其数值基于充放电策略和风功率输出确定。VRB优先动作模式中，LiB仅针对充放电功率越限部分能量；而LiB主要动作模式下，在LiB启动且其充放电功率及其变化率和SOC均满足平抑条件时，将作为平抑能量主体。 

2.2 约束条件

    约束条件主要包括充放电功率约束、SOC约束。

    (1)充放电功率约束

2.3 求解算法

    本文采用鲁棒性强、计算效率高的粒子群优化算法（Particle Swarm Optimization，PSO）对算例进行求解，并对其进行适度改进，以克服动态边界问题，同时递进优化的区间计算量相对较小，利于发挥PSO搜索精度高和收敛效果好的优势。具体模型求解步骤为：

    (1)根据递进协调控制算法和本步长数据确定优化目标函数；

    (2)设置粒子群维数D、最大迭代次数M_max、收敛精度σ_thresh，同时初始化粒子群位置x和速度v，并给定初始SOC_int-LiB、SOC_int-VRB数值；

    (3)根据既定充放电策略和目标函数计算各粒子适应度值M；

    (4)将各粒子适应度值与自身粒子极值及全局粒子极值比较，若适应度值较小，则更新各粒子个体极值e_best及全局例子适应度极值g_best；

    (5)判断当前计算是否满足收敛条件，若是，则提取当前P_LiB、P_VRB即为最优充放电功率；若否，则更新各粒子位置x及速度v，并重复步骤(3)～(5)。

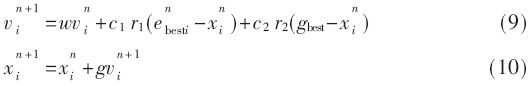
其中n为当前循环次数，c₁、c₂为粒子权重系数，w为惯性权重，r₁、r₂为（0，1）内均匀分布随机数，x_i、v_i为第i维粒子的位置与速度，g为约束因子。  

3 验证分析

    为验证本文方法有效性，基于风电场实际运行数据进行分析，该风场装机容量75 MW，储能电站中LiB额定容量配置为10 MWh，VRB为4.5 MWh，各采样点间隔为5 min。运行参数中，LiB的SOC运行允许限值为[0.1，0.9]，而VRB的SOC运行限值为[0，0.95]；LiB的充放电功率限值均为13 MW，而VRB的充放电功率均为9 MW；经统计该风场功率特征，E_min-discha取值为-1.1 MWh，而E_min-cha取值为1.0 MWh。

    (1)算例1：提取该风电场某年度5月份运行数据，基于本文所提方法，计算结果如表1所示。

    如表1所示，本文所提方法在相关评价指标上均有大幅改变，其中充放电启动因采用VRB独立承担弱能量区间的充放电任务，LiB的启动次数显著降低，减少了77.9%；平抑效果方面，由于LiB和VRB的协调配合，使得平抑后的功率偏移量方差降低41.7%，保证了平抑效果；目标函数数值M降低46.9%。

    选取一定时间截面区间P_LiB(t)、P_VRB(t)显示如图2所示，SOC_LiB(t)、SOC_VRB(t)如图3所示。充放电功率方面，可以看出，P_LiB(t)和P_Uc(t)的协调使得各自充放电功率越限次数降低，同时P_Uc(t)独立承担弱能量区间的充放电使P_LiB(t)有效减少充放电启动，而在两者同时充放启动的状况下，P_LiB(t)可承担更多的平抑任务；结合图3中SOC可以看出，其SOC_LiB变化较SOC_VRB要小，LiB适合于浅充浅放，而VRB则可发挥其SOC可大范围变化的优势。

    (2)算例2：提取该风电场某年度10月份运行数据，计算结果如表2所示。选取一定时间截面区间P_LiB(t)、 P_VRB(t)、SOC_LiB(t)、SOC_VRB(t)分别如图4、图5所示。

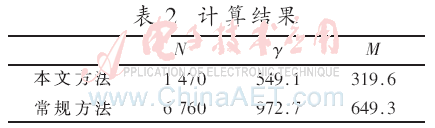
    表2中相关评价指标同样均有较大幅度优化，其中LiB的启动次数相比减少78.3%，而平抑后的功率偏移量方差降低43.5%；同时本文目标函数数值M降低50.8%。总体而言达到了本文方法的目标；在充放电功率和荷电状态方面，该算例同样较好地实现了本文方法的优化目标。当放电平抑任务较重、需较大容量放电容量时，此时两者同时启动，LiB承担较大放电容量；但若其SOC接近下限，此时VRB则承担起了剩余放电功率。

    综上所述，本文提出的考虑功率预测的储能电站动态充放电策略可有效实现递进控制区间的运行最优化。所提方法可保证各介质SOC运行状态及平抑效果的前提下有效减小LiB的充放电转换次数，充分发挥VRB的介质特性。

4 结论

    本文考虑将超短期风功率预测引入储能电站的控制过程，同时提出VRB优先动作或LiB主要动作的充放电策略，目的是通过递进式的区间优化实现储能电站的动态经济控制；通过构建递进区间控制的优化目标函数，并考虑实际条件约束，给出了基于粒子群算法的实现流程和求解步骤。利用实际风电场运行数据进行验证，根据平移后的功率偏移量、SOC运行区间等多个评价指标的分析结果，表明本文控制方法对储能电站的充放电转换次数及平抑效果等均具有显著效果。本文所提控制方法高效可靠，具有一定的理论价值和实际应用价值。

参考文献

[1] 肖湘宁，陈征，刘念.可再生能源与电动汽车充放电设施在微电网中的集成模式与关键问题[J].电工技术学报，2013，28(2)：1-14.

[2] BARTON J，INFIELD D.Energy storage and its use with intermittent renewable energy[J].IEEE Trans.on Energy Conversion，2004，19(2)：441-448.

[3] 高明杰，惠东，高宗和，等.国家风光储输示范工程介绍及其典型运行模式分析[J].电力系统自动化，2013，37（1）：59-64.

[4] 施琳，罗毅，涂光瑜，等.考虑风电场可调度性的储能容量配置方法[J].电工技术学报，2013，28(5)：120-127.

[5] 袁铁江，陈洁，刘沛汉，等．储能系统改善大规模风电场出力波动的策略[J]．电力系统保护与控制，2014，42(4)：47-53.

[6] TELEKE S，BARAN M E，BHATTACHARYA S，et al.Optimal control of battery energy storage for wind farm dispatching[J].IEEE Trans on Power Systems，2010，25(3)：787-794.

[7] 蒋凯，李浩秒，李威，等.几类面向电网的储能电池介绍[J].电力系统自动化，2013，37(1)：47-53.

[8] 杨珺，张建成，周阳，等.针对独立风光发电中混合储能容量优化配置研究[J].电力系统保护与控制，2013，41(4)：38-44.

[9] 张国驹，唐西胜，齐智平.平抑间歇式电源功率波动的混合储能系统设计[J].电力系统自动化，2011，35（20）：24-28.

[10] 程时杰.大规模储能技术在电力系统中的应用前景分析[J].电力系统自动化，2013，37（1）：3-8.