0 引言

    双有源全桥DC-DC变换器被广泛应用于涉及电能储存的系统中，例如混合电动汽车驱动系统、新能源发电储能系统、不间断电源等^[1，2]。为保证储能系统电压或功率输出稳定或是跟随给定输出，应设计高动态性能控制策略。而建立系统的数学模型是控制器设计中的重要环节^[3]。所以，对变换器进行精确的建模具有重要意义。

    国内外专家对双有源全桥DC-DC变换器进行了大量的分析和研究。其中文献[3]分析了功率传输工作特性，建立了双有源全桥DC-DC变换器状态空间平均模型，并分析了电感和电容对动态和稳态特性影响；文献[4]应用离散建模方法，建立了双有源全桥DC-DC变换器精确的离散小信号模型，设计了双闭环控制器。

    从上述文献中可以看出，建立开关变换器模型常用的建模方法是状态空间平均法、电路平均法及数据采样建模法等，其中前两种建模方法简单实用，但忽略一个开关周期内状态变量的波动^[5]。在双有源全桥双向DC-DC变换器中电感电流波动较大，应用状态空间平均法建模需降阶处理，降低了模型准确度。数据采样建模方法虽然精确度高，但需要获得一个周期的稳定值，计算量大，表达式复杂。

    基于以上问题，本文采用一种适合于谐振变换器的建模方法^[6]建立双有源全桥变换器的小信号模型。广义状态平均法将一个时变的状态方程转换为线性时不变的状态方程。文中计算分析变换器工作模态，应用广义状态平均法建立系统的小信号模型和稳态模型；通过仿真实验比较广义状态平均法、状态空间平均法建立的模型与实际拓扑稳态输出的误差，验证广义状态平均法的准确性和有效性；最后根据广义状态平均法建立的模型设计闭环控制器。

1 广义状态空间平均法

    信号分析中可知，若信号x(t)满足傅里叶变换的条件，则信号x(t)在时间段[t-T，t]中，可以通过式(1)得到信号x(t)傅里叶级数的第k次系数形式。

    当窗口函数在信号的时间轴上滑动，得到的傅里叶系数x_k(t)是关于变量t的函数。

    傅里叶级数是离散频率的傅里叶变换，所以合理利用傅里叶变换的性质，傅里叶变换的性质中最重要的是微分性质，通过微分性质得到变量的状态方程，由傅里叶系数表达式得到第k次傅里叶系数的微分方程：

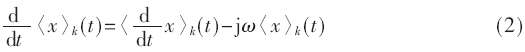
    广义状态空间平均法建模用到的傅里叶变换另一重要性质即它的频域卷积定理，若一个信号的表达式是f(x₁，x₂)=x₁ x₂，其中x₁、x₂都是关于时间t的函数且x₁、x₂的傅里叶变换存在，则函数f(x₁，x₂)的傅里叶变换为：

    应用上述性质便于求得系统状态量的傅里叶级数系数。开关变换器在每个工作模态都是线性时不变系统，根据一个开关周期内变换器的工作模态，列出时域状态方程：

其中u(t)是一个开关周期T内关于时间t的函数。

    将广义状态空间平均法应用在电力电子变换器中，分别对式(4)等号两侧求第k次傅里叶系数，得到：

    进一步简化描述系统的状态方程，应用傅里叶系数的微分性质，得到第k次傅里叶系数的状态方程，通过系统时域状态方程得到等号右侧关于系数〈x〉_i、〈u〉_i的函数。如式f(x，u)中有二次项或多项式乘法，利用傅里叶变换卷积性质进一步简化。

    通过信号分析可知，幅值较大的低阶次的傅里叶系数能够充分描述系统的低频特性。考虑到系数越多，能更精确描述原系统特性，为了简化计算，减少状态空间方程的阶次，只分析信号的低阶分量。

2 双有源全桥双向DC-DC变换器的建模

    双有源全桥双向DC-DC变换器的拓扑如图1所示，R_c1、R_c2分别为电容C₁、C₂的内阻，L是高频变压器的漏感折算到一次侧的等效漏感，R_L是变压器内阻的等效电阻。变压器原副边绕组的匝数比为N，本文为了便于推导，设N=1。

    变压器两侧的电压v_ab、v_cd在稳态时可以近似认为是两个交流方波。双有源桥DC-DC变换器工作在稳态时，在一个开关周期T内，变压器两端电压和电感电流理想波形如图2所示，D_φ是隔离变压器原副边基波电压移相角φ与π的比值。

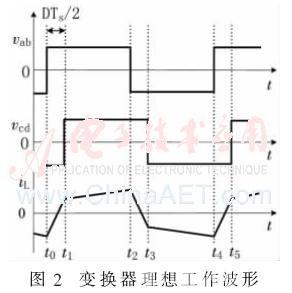
    由于开关管的开关过程较短，为了便于分析,假设开关过程瞬间完成。从图2中可以看出变换器在一个周期内有4种工作模态，由4种模态的状态空间方程，得到一个开关周期T内的状态方程：

    在双有源全桥工作在功率正向传输模式时R_c1=R_c2=R_s1=0，输入为V₁。因此，用广义状态空间平均法建立的模型包含电感电流i_L一次傅里叶系数和输出电压u_c2的零次傅里叶系数。由式(6)得到广义状态空间平均模型：

    在广义状态空间模型中，状态变量是变换器原变量的傅里叶级数系数，分别列写由状态变量实部和虚部组成的状态方程，得到变换器模型的三阶状态空间方程表示为：

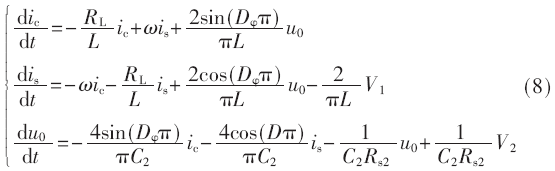
    由微分方程(8)得到变换器的稳态工作点，假设开关变换器的静态工作点各变量大小为I_c、I_s、U₀。若在稳态工作点附近对输入变量、状态变量和变压器原副边移相比控制量引入低频小信号扰动，使变换器的状态量和输出变量发生微小变化。用泰勒级数展开进行线性化处理，得到由系统的小信号模型。系统广义状态空间平均小信号模型状态矩阵和输出矩阵如下：

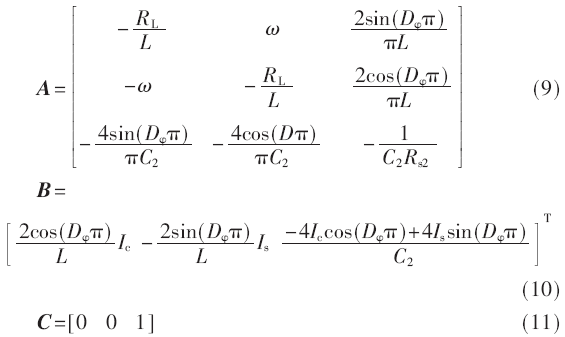
    根据双有源全桥双向DC-DC开关变换器的小信号状态空间描述方程，利用式(12)求解电压uc2关于移相比D_φ的传递函数。

3 仿真结果

    本文通过MATLAB仿真分析验证广义状态空间平均法建立双有源全桥双向DC-DC变换器模型的准确性和有效性，参数见详表1。

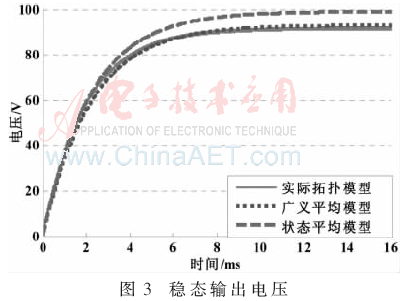
    图3中比较了广义状态空间平均法模型、状态空间平均法模型的输出电压与开关变换器物理模型的开环输出电压，其中控制输入移相比D_φ=0.4。从图3中可以看出，广义状态空间平均模型相比状态空间平均模型能更准确模拟实际拓扑模型的稳态特性与动态特性。

    通过建立系统的小信号模型设计系统的闭环控制器，使系统获得较好的动态性能并减小系统的稳态误差。图4给出了由广义状态空间平均法和状态空间平均法两种建模方法建立的模型的开环系统控制-输出伯德图。从图4中可以看出，两种建模方法建立的模型伯德图的最大不同在系统的高频段，产生这种差别的原因是状态空间平均法忽略了电感电流的波动。

    系统伯德图表征了闭环系统的动稳态特性及抑制噪声的能力。因此，为改善开环系统的动态性能，开关变换器的闭环系统的截止频率一般在开关频率的1/5~1/20范围内。为获得满意的动态过程，闭环系统的相角裕度为45°~70°，增益裕度在10 dB以上。根据上述要求设计闭环系统的PI控制器。图5为闭环系统的伯德图，由图中可知满足控制器设计要求。

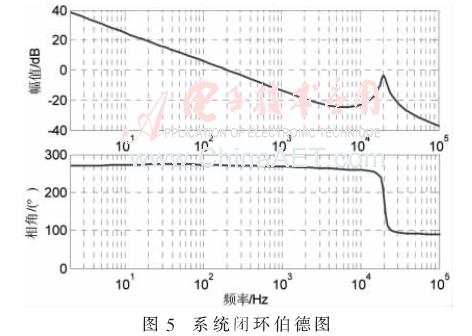
    图6为变换器闭环控制系统的输出电压和负载电流。在10 ms时加入负载扰动负载电流突变，输出电压快速达到稳定。图6中闭环系统的输出电压与图3中开环系统的输出电压相比较可知，设计的闭环控制器使系统响应速度快，准确跟随给定参考值，有很好的抗干扰能力。

4 结论

    本文基于广义状态空间平均法建立的双有源全桥双向DC-DC变换器模型准确、有效。基于广义状态空间平均法能准确建立双有源全桥双向DC-DC变换器的稳态及动态模型；通过合理的简单近似解决了建模准确性和计算量过大的矛盾；双有源全桥DC-DC变换器的广义状态空间模型为设计满足稳态及动态性能指标的控制器提供了理论基础。

参考文献

[1] INOUE S，AKAGI H.A bi-directional DC/DC converter for an energy storage system[C].Applied Power Electronics Conference，APEC 2007-Twenty Second Annual IEEE.IEEE，2007：761-767.

[2] BAI H，MI C，WANG C，et al.The dynamic model and hybrid phase-shift control of a dual-active-bridge converter[C].Industrial Electronics，2008.IECON 2008.34th Annual Conference of IEEE.IEEE，2008：2840-2845.

[3] 欧阳长莲.DC-DC开关变换器的建模分析与研究[D].南京：南京航空航天大学，2004.

[4] KRISMER F，KOLAR J W.Accurate small-signal model for an automotive bidirectional dual active bridge converter[C].Control and Modeling for Power Electronics，2008.COMPEL 2008.11th Workshop on.IEEE，2008：1-10.

[5] MIDDLEBROOK R D，CUK S.A general unified approach to modelling switching-converter power stages[J].International Journal of Electronics Theoretical and Experimental，1977，42(6)：521-550.

[6] WANG P，LIU C，GUO L.Modeling and simulation of full-bridge series resonant converter based on generalized state space averaging[C].Applied Mechanics and Materials，2013：1828-1832.