摘 要： 摄像机标定技术已被广泛地应用于三维重建技术中。针对标定时需要手动确认角点比较耗时且可能存在误差的问题，本文提出一种基于双旋转模板的黑白棋盘角点检测算法。该算法首先通过Harris算法获得初始角点，然后通过构造旋转模板对获得的角点进行迭代筛选，最终求解得到符合标定要求的角点。实验证明本文算法不仅具有较高的稳定性，还提高了黑白棋盘上有效角点的检测精度和效率。

　　关键词： 三维重建；摄像机标定；黑白棋盘；角点检测；Harris

0 引言

　　三维重建是计算机视觉研究的核心问题之一。按照是否求解摄像机参数，将三维重建分为基于标定的[1-2]和基于未标定的[3]重建技术。基于未标定的重建技术需要通过两幅或多幅图像求解摄像机的运动参数和场景中特征点的三维坐标，算法较为复杂。基于标定的重建技术需要提前对摄像机进行标定，对设备要求低，操作简单，重建效果满足用户要求。摄像机标定技术是要精确求解摄像机内外参数，从而恢复二维图像携带的三维场景信息，是三维重建系统的重要模块，其求解结果的好坏、精确程度和实时性直接影响整个系统的性能。通常，标定过程需要借助标定物，如黑白棋盘。针对黑白棋盘的角点检测技术对摄像机标定工作非常重要，是摄像机标定的前提和基础。所谓角点，就是图像中灰度变换较大的点。

　　黑白棋盘的角点检测技术一般用于三维重建中相机标定部分，能够将人们从繁杂的手动标定工作中解放出来，提高标定精度。目前，学者们已经对该技术进行了大量研究。参考文献[4]中的Harris角点检测算法使用灰度的高斯梯度作为响应值判断棋盘格图像中的角点，该方法简单有效，但容易受到棋盘角点附近其他高梯度像素点的影响。参考文献[5]提出了一种自动识别黑白棋盘上角点的角点检测方法，但当遇到复杂背景时，该方法仍然容易受到非棋盘角点的影响。参考文献[6]依据方格边缘的交点形成角点这一性质，先对图像中的边缘进行检测，再利用Radon变换确定边缘的位置，最后通过求取边缘交点的方法确定角点坐标。该方法对边缘提取算法依赖性较大，容易受到镜头畸变情况的影响。

　　针对上述问题，本文提出了一种基于双旋转模板的黑白棋盘角点检测算法，该算法首先采用Harris算法[7-9]对包含黑白棋盘的图像进行角点检测，获得初步的角点集，通过构造双旋转模板对获得的角点进行迭代筛选，根据检测结果自适应调节参数。该算法具有稳定性高、抗噪声、自适应性强等特点，可应用于镜头存在畸变、实际背景复杂等特殊的摄像机标定情况。

1 本文算法

　　1.1 Harris角点检测算法

　　本文算法获得初始的角点集合由Harris算法获得，该方法基本原理描述如下：

　　首先建立下面矩阵：

　　其中， I为输入图像，表示图像I在x方向的导数，missing image file表示图像I在y方向的导数。通过分析上面矩阵可以看出，如果一个像素点对应的矩阵M的两个特征值都很大，则在该点向任意方向上的一个很小的移动都会引起灰度值的较大变化，则认为该点是一个角点。通过计算如下的响应函数值来判断角点：

　　其中，det(.)为取行列式值，trace(.)为取矩阵的迹，k一般设为0.04。求出R的值，若为正则对应点为角点，若为负则是一般边界点，当其绝对值很小时为平坦区。

　　该算法易受噪声的影响。为了减小噪声的干扰，在对图像进行偏导计算以后用高斯滤波器对数据进行平滑。按此方法求出的角点数量很多。为了减少匹配计算量，可以对想要获得的角点数量进行限制。限制方法是确定一个阈值，仅仅选取R值大于这个阈值的点作为角点[7]。Harris算法作为本文算法的第一步，使本文算法具有了旋转不变性、抗噪性等特点。

　　1.2 基于双旋转模板的角点迭代筛选

　　当用Harris算法进行角点检测之后，对获得的点集采用本文提出的基于双旋转模板的方法进行二次检测。首先对图像二维像素(i，j)求解如下两个函数：

　　其中，Ii (i=1,2,3,4)表示以O(i，j)为中心沿着di方向上遍历的像素灰度值，如图1。若沿着d1和d4方向上像素点灰度值的累加和与沿着d2和d3方向上像素点灰度值的累加和存在较大的差异，则可认为该点为黑白棋盘上的角点。实际应用中需要构建如下式所示的两个多阶方矩阵：

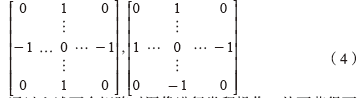
　　通过上述两个矩阵对图像进行卷积操作，从而获得两个集合C1和C2，由于本文迭代过程中需要对式（4）进行旋转处理，因此称式（4）为双旋转模板。

　　然后，需要通过自适应阈值约束式（3）的结果，求解最有可能为棋盘上的角点集，自适应阈值的计算如下：

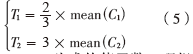
　　mean(.)为求均值函数。理想的角点必须满足其对应c1值大于T1，同时其对应的c2值小于T2。

　　本文算法的具体实现步骤为：

　　⑴采用1.1节所述的Harris算法对图像进行角点检测，获得初步角点集合S。设置迭代次数为t，根据式（4）构造双旋转模板，模板大小设为2n+1。

　　⑵采用双旋转模板对图像中的角点集合S进行卷积操作，获得满足自适应阈值T1和T2的点集合P。

　　⑶取半径r，并合并P中距离相近的角点，最终得到集合Q。

　　⑷判断是否超过迭代次数，若未超过迭代次数则双旋转模板进行旋转调整，旋转角度为θ，返回步骤（2）；若超过迭代次数则判断检测结果是否为预测结果，即得到的Q中的角点数量m是否与预测的相符，若为预测结果则转到步骤（6），否则跳到步骤（5）。

　　⑸算法失败，重新设置相关参数或进行手动角点标定。

　　⑹算法成功，查看效果。

　　本文算法计算简单，具有较高执行效率，一般当t≥3时即可得到理想效果，迭代收敛的条件为：Q的角点数量等于预测获得的角点数量，该数量可通过黑白棋盘的先验信息得到。

2 实验仿真与分析

　　本文将在Matlab平台（CPU Intel双核主频2.66 GHz）进行模拟仿真实验。实验中使用自制的黑白棋盘格，黑白棋盘格由13×14个方格组成，拍摄的图像的分辨率为632×471，本文将与手动获得黑白棋盘角点的方法进行比较。手动获取黑白棋盘角点多用于以往的摄像机标定，其步骤为首先手动确认棋盘上4个边界点，如图2（a）所示，然后自动生成网格点，如图2（b）所示，最后通过算法自动校正，如图2（c）所示。该方法并不属于角点检测方法，而且当处理多幅图像时，处理相当耗时。

　　采用本文算法自动对黑白棋盘格进行角点检测，主要参数设置为：t=3，n=10，m=156，r=5，θ=20。首先进行Harris角点检测，获得初始结果如图3（a）、（b）所示，然后进行基于双旋转模板的迭代筛选，最终得到结果如图3（c）、（d）所示。通过实验可知，本文方法与手动标定方法结果一致，其运行稳定，效率高。

3 结论

　　本文提出的针对黑白棋盘的角点检测算法能够应用于立体视觉技术、三维物体重建等领域的摄像机标定过程中，该算法首先采用Harris算法获得初始角点集，然后构造双旋转模板，通过卷积操作对角点进行迭代筛选，最终得到摄像机标定所需的黑白棋盘角点。实验结果证明，该算法稳定性强，准确度高，计算量小，具有旋转不变性、抗噪性等优势，可以将研究人员从繁琐的手动获取棋盘角点信息的工作释放出来，具有较强的现实意义。

　　参考文献

　　[1] Zhang Zhengyou. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11):1330-1334．

　　[2] 杨幸芳,张梦文,严凯,等. 一种基于参数约束关系的工业相机的线性标定法[J]. 微型机与应用, 2014,33(11):38-40.

　　[3] 赵宏宇,李燕华,侯振杰,等. 基于鲁棒估计灭点分层重建的研究[J]. 微型机与应用, 2011,30(9): 31-35.

　　[4] Harris C, Stephens M. A combined corner and edge detector[C]. Proceedings of the Fourth Alvey Vision Conference. Manchester, 1988: 147-151.

　　[5] 刘阳，王福利，常玉清，等. 黑白棋盘格角点检测算法[J]. 东北大学学报(自然科学版)，2007, (8):1090-1093.

　　[6] 胡海峰,熊银根. 一种基于两次Radon变换检测棋盘格方格点的新算法[J]. 中山大学学报(自然科学版), 2003, 42(2) : 23- 26.

　　[7] 唐烁,缪源. 基于Harris角点的图像匹配算法[J]. 微型机与应用, 2013, 32(2):41-43.

　　[8] 罗桂娥,李映. 基于均匀角点匹配的基础矩阵估计方法[J]. 微型机与应用, 2013, 32(7):8-9.

　　[9] 熊显名,任娟娟. 黑白棋盘格中的角点提取算法的研究[J]. 微型机与应用, 2014, 33(9):66-69.