0 引言

    分布式电源接入对改善配电网电能质量、提高供电可靠性、降低线路损耗等具有重要作用^[1-3]。福建省山区供电网架相对薄弱，系统供电可靠性低，低电压及线损过高问题较为突出。加大福建省山区分布式电源的开发力度，对于解决上述问题具有重要意义。然而，分布式电源接入容量及位置不同会带来不同的影响。如何确定合适的接入容量及位置，保证系统更加经济、可靠地运行，是目前分布式电源接入系统研究的重点内容^[4-7]。

    分布式电源发电的波动性与随机性，潜在地增加了分布式电源接入配电网系统的难度。智能算法的产生，为解决优化问题提供了有效途径。文献[8]基于线损最小化的目标，针对不同种类分布式电源建立了系统优化模型，利用改进遗传算法进行模型求解，但遗传算法容易产生早熟现象，陷入局部最优解；文献[9]利用改进的粒子群算法对分布式电源的接入进行优化；文献[10]考虑到系统综合费用，提出量子微分进化算法对分布电源进行优化配置。但混合后的改进粒子群算法及量子微分进化算法参数较多，编程困难。

    萤火虫算法作为新颖的智能优化算法，其仿生原理简单，系统参数少，易于编程实现，具有较强的收敛能力及全局寻优能力^[11]，已成功应用于微网中微源负荷博弈模型的优化求解^[12]及分布式风电的优化配置^[13]。本文在福建省山区典型配电网供电模式下，以网络损耗最小为目标，建立了福建山区配电网系统网损目标函数模型，提出利用萤火虫优化算法进行模型求解，得出了适用于福建省山区配电网分布式电源最优接入容量及位置的寻优方法。

1 分布式电源接入优化模型

    分布式电源的接入会对配电网潮流分布产生一定的影响，系统潮流分布的不同直接影响着配电网系统的稳定及经济性。本文所建优化模型考虑到配电网系统的潮流稳态平衡、节点电压约束、分布式电源有功功率约束、线路支线功率约束等约束条件。

1.1 潮流分析

    分布式电源接入配电网系统模型如图1所示。

    配电网系统中节点i流出的有功及无功功率P_i、Q_i如式(1)、式(2)所示：

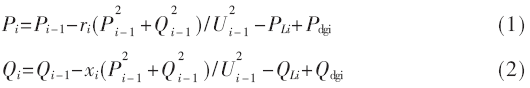
其中，U_i是节点i的节点电压；r_i、x_i是节点i与其下一节点所联的支路电阻及支路电抗；P_Li、Q_Li是节点i的有功负荷及无功负荷；P_dgi、Q_dgi为节点i处分布式电源注入的有功功率及无功功率。

    根据我国国家电网的相关技术规定，配电网系统中10 kV与380 V电网线路节点电压不得超过1.07 p.u。因此，考虑到分布式电源接入对线路节点电压的影响，应保证分布式电源接入系统后，接入点处的线路节点电压不越限。文献[5]中考虑到节点电压越限的情况，给出了分布式电源在电压不越限下较为实用的最大准入容量的计算方法，在此不再赘述。

1.2 目标函数

    分布式电源接入配电网要保证系统更加经济稳定地运行，接入容量与位置的选取则显得至关重要。本文所建配电网系统网损目标函数如式(3)所示。

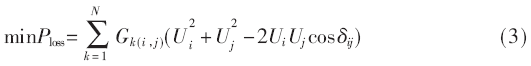
其中，N表示该配电网系统中电网支路的条数， i、j为第k条支路两端的节点编号，G_k(i，j)则为配电网支路k的电导， δ_ij为节点i、j的电压相角差。

1.3 模型约束条件

    本文所建立的分布式电源最优接入优化模型中，考虑到系统潮流稳定、节点电压、分布式电源输出功率及线路功率等约束条件，各等式约束及不等式约束条件如下文所述。

1.3.1 等式约束条件

    配电网系统运行稳定时，各节点及线路上的潮流应处于动态稳定的状态，等式约束条件如式(4)所示。

1.3.2 不等式约束条件

    系统不等式约束条件应考虑到分布式电源接入后，保证接入点电压跌落及越限在合适的范围内、分布式电源接入容量不超过其最大发电容量、系统线路功率在线路最大承载功率下。各不等式约束方程如下所示。

    (1)节点电压约束

式中：U_imax和U_imin分别为配电网系统中第i个节点电压的上限及下限值，即在分布式电源接入配电网系统后，接入点电压不得超过1.07 pu。

    (2)DG功率约束

2 萤火虫算法及优化模型的求解

2.1 萤火虫算法

    剑桥学者Yang通过模拟自然界中萤火虫的发光特性，于2008年提出了萤火虫算法。该随机优化算法的实现过程主要如下所述：

    首先对萤火虫初始化，对不同位置下的萤火虫进行评价，选出萤火虫中局部相对吸引度最大的个体和整个萤火虫中亮度最大的个体；然后萤火虫向其周围亮度较高的个体移动，移动后萤火虫更新自己的位置，同时根据相应的位置更新各自的亮度及吸引度；经过数次移动后，萤火虫将聚集在亮度最高的位置上。

2.2 分布式电源最优接入容量与位置求解步骤

    萤火虫优化算法中，萤火虫的亮度与各自的目标函数值有关，目标函数值越大的萤火虫其亮度越高，相应的吸引度也就越强。在福建省山区分布式电源接入配电网系统优化模型中，本文以福建山区配电网系统网络损耗最小为目标函数。因此，在萤火虫优化算法求解过程中，令：

    萤火虫优化算法求解后，寻优的最优值即为对应的配电网系统网络损耗的最小值。

    在福建省山区配电网分布式电源接入容量或位置确定时，确定最优接入位置或容量实现网损最小化的步骤如下所示：

    (1)输入福建省山区配电网系统网损目标函数minPloss=设置萤火虫算法中萤火虫的个数、光吸收系数、最大吸引度、优化迭代次数、系统扰动因子等计算参数。

    (2)设置算法中萤火虫的初始位置集合为X=(x₁，x₂，…，x_n)，其中当分布式电源容量确定时，集合X代表分布式电源接入位置集合，x_i表示分布式电源接入配电网中的第i个结点，i∈n；当分布式电源接入位置确定时，X代表分布式电源接入容量集合，x_i表示分布式电源在配电网中第i个节点的接入容量，i∈n。

    (3)计算萤火虫在不同位置xi时，萤火虫的最大亮度、吸引度、萤火虫之间的距离、移动方向等，根据移动的距离及方向对萤火虫的位置进行更新。

    其中：萤火虫的亮度I表示为：

    I₀为萤火虫的最大萤光亮度，γ为光强吸收系数，β₀为最大吸引度，x_i、x_j为萤火虫i和j所处的位置；α和rand均为扰动随机参数，用于扩大萤火虫的搜索空间，避免过早陷入局部最优。

    (4)判断萤火虫位置x_i是否满足收敛判据ε。若满足，则将萤火虫新位置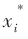作为最佳位置；若不满足，则返回步骤(3)，继续改变萤火虫位置，进行下一轮的位置更新。

    (5)短路电流校验，分布式电源接入容量或位置确定后，校验系统短路点短路电流是否超过线路最大允许短路电流，若不满足校验，则返回步骤(2)。

    (6)输出

    输出萤火虫的最优位置，即在分布式电源接入容量确定时，分布式电源最优的接入位置，或在分布式电源接入位置确定时，分布式电源最优的接入容量。

    算法求解流程如图2所示。

3 算例分析

    目前，福建省山区农村中压配电网主要以辐射状式供电结构为主，已形成“八爪鱼”式的电网结构，即一个乡镇的中心电源点馈出若干条主线，主线上根据负荷分布馈出若干条小线径的分支线，分支线上又根据负荷分布馈出若干条更小线径的分分支线，系统结构如图3所示。主干线与主干线、分支线与分支线、主干线与分支线之间联络极少，几乎都是辐射状结构。

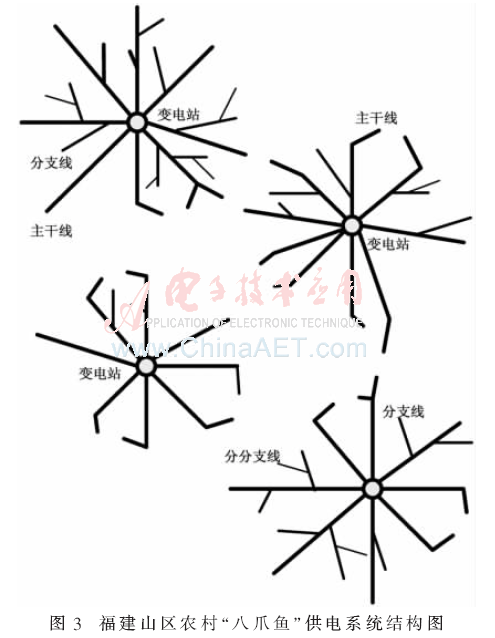
    为了验证本文所提萤火虫优化算法的有效性，取福建省山区配电网“八爪鱼”系统结构上的一条中压馈线进行分析，在该馈线上取出33个节点，各节点分布如图4所示。

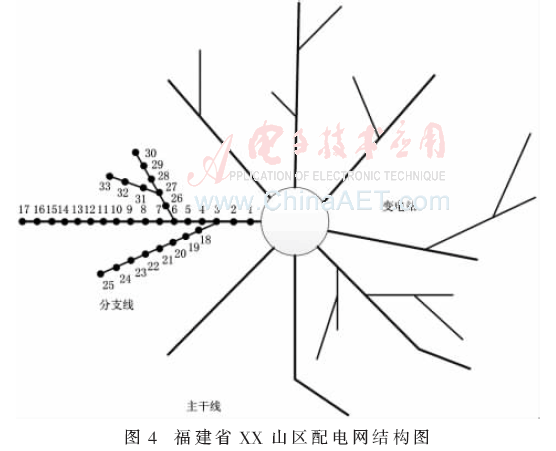
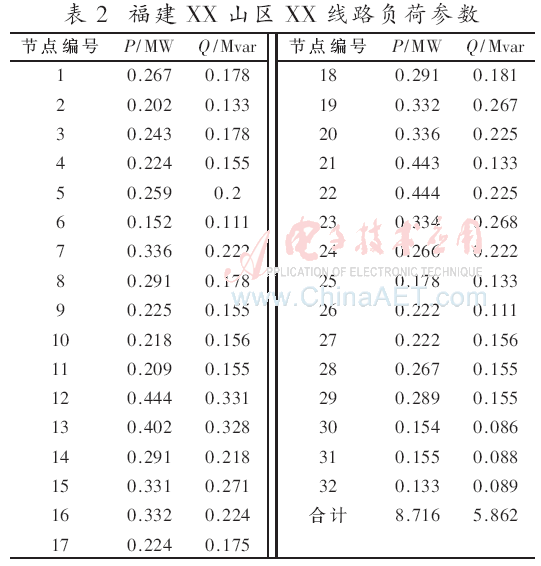
    在所分析的供电线路上，系统供电变电站处系统电压为10.6 kV，线路额定电压为10.0 kV。该配电网供电线路上共有4条分支线路，最长分支线路(节点1-17)线路长度约10 km。该供电网络为架空单辐射网络，主干线路由JKLYJ-240架空线组成，最大输送容量为10.5 MVA，正常运行时网损率约8％。算例参数如表1和表2所示。

    在萤火虫优化算法中，本文选取200个萤火虫，设置光强吸收系数γ=7.812 5×10^-7，最大吸引度和步长因子分别取为β₀=0.9，α=0.8，rand为[0，1]上服从均匀分布的随机因子，迭代次数为100次。

    本次以主干线（节点1-17）为例进行算例分析，从图4可看出，该供电线路上的分支线路多位于主干线路的前端。因此，主干线路前端的负荷比主干线路后端的负荷多。各主干线路上各节点的最大准入容量如图5所示。

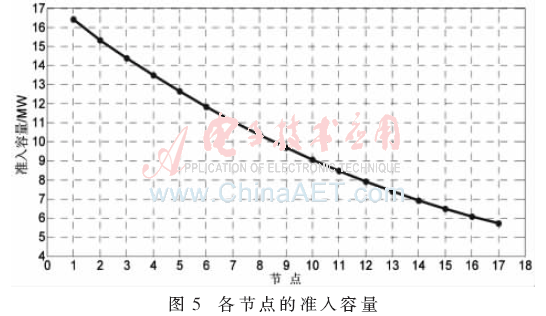
    通过计算得主干线末端17节点处的最大准入容量为5.73 MW。从图5可以看出，越靠近主干线路前端的节点，分布式电源的准入容量就越大，可带负荷也就越多；反之，在系统主干线路的末端，系统负荷减少，同时为了避免潮流的逆向传输，末端分布式电源的最大准入容量相对较小。

    当分布式电源位置确定时，通过计算萤火虫在不同位置时的亮度、吸引度、萤火虫之间的距离、移动方向等，经过数次寻优，得到了萤火虫最佳位置点。在萤火虫算法中，萤火虫的位置集合即为分布式电源的容量集合。

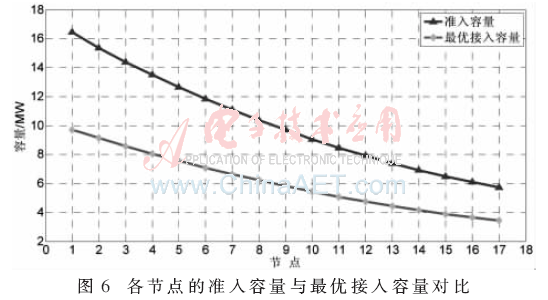
    各节点处的最大准入容量与最优接入容量对比如图6所示。从图中可看出，分布式电源的最优接入容量同样沿主干线路逐渐降低，即在主干线路的末端考虑到所带负荷容量及潮流分布的情况，接入主干线路末端的分布式电源的最优接入容量最小。如果该节点的最优接入容量超过了该节点的最大准入容量，则将准入容量作为该节点的最优接入容量；若该节点的最优接入容量小于其准入容量，则认为已确定的最优接入容量可实现系统网损最小，分布式电源接入后使配电网处于经济的运行状态。以主干线路上的末端17节点为例，通过萤火虫算法的多次寻优，得出17节点最优的接入容量为3.75 MW，低于其最大准入容量5.73 MW。因此， 17节点在接入3.75 MW容量时，满足节点电压约束条件，同时在该接入条件下，使得配电网系统网络损耗最小，提高了系统的经济性。

4 结论

    本文在福建山区配电网典型的“八爪鱼”供电模式上，对分布式电源的接入模型进行了研究，同时采用萤火虫算法进行优化求解。算例结果验证了萤火虫算法在分布式电源接入优化求解中的有效性，该算法简单，易实现。分布式电源最优接入容量与位置的研究，有助于指导福建省山区配电网的规划，对于山区配电网具有重要的经济价值和现实意义。

参考文献

[1] 梁有伟，胡志坚，陈允平.分布式发电及其在电力系统中的应用研究综述[J].电网技术，2003，27(12)：71-75.

[2] 王志群，朱守真，周双喜，等.分布式发电对配电网电压分布的影响[J].电力系统自动化，2004，28(16)：56-60.

[3] 裴玮，盛鹍，孔力，等.分布式电源对配网供电电压质量的影响与改善[J].中国电机工程学报，2008，28(13)：152-157.

[4] 刘志昱，黄伟.基于稳态分析和区间层次分析法的分布式电源最佳位置确定方法[J].电网技术，2011，35(11)：57-61.

[5] 文升，顾洁，程浩忠，等.分布式电源的注入容量与优化布置的实用方法[J].电力自动化设备，2012，32(10)：109-114.

[6] 王建国，杨秀苔.考虑分布式电源接入的新农村电网规划模型[J].电网技术，2012，36(3)：264-268.

[7] 钟嘉庆，叶治格，卢志刚.分布式发电注入容量与接入位置的优化配置分析[J].电力系统保护与控制，2012，40(7)：50-55.

[8] 胡吟，韦钢，言大伟，等.分布式电源在配电网中的优化配置[J].电力系统保护与控制，2012，40(11)：100-105.

[9] 刘波，张焰，杨娜.改进的粒子群优化算法在分布式电源选址和定容中的应用[J].电工技术学报，2008，23(2)：103-108.

[10] 于青，刘刚，刘自发，等.基于量子微分进化算法的分布式电源多目标优化规划[J].电力系统保护与控制，2013，41(14)：66-72.

[11] Yang Xinshe.Firefly algorithm for multimodal optimization[C].Proc of the 5th International Conference on Stochastic Algorithm：Foundations and Applications.Berlin：Springer Verlag，2009：169-178.

[12] 王晶，王宗礼，陈骏宇，等.基于萤火虫优化算法的微网源-荷博弈模型及分析[J].电力系统自动化，2014，38(21)：7-12.

[13] 倪健，黄红程，顾洁，等.基于萤火虫算法的分布式风电源优化配置[J].华东电力，2014，42(10)：2074-2080.