摘 要： 逻辑模型树（LMT）算法是基于树归纳和逻辑回归的一种分类算法。为验证LMT算法的优势，利用3个UCI标准数据集建模，将LMT算法与其他决策树方法进行对比分析。针对LMT算法在建立逻辑回归模型时会导致较高的计算复杂性的问题，研究利用赤池信息量准则改进LMT算法，提升算法时间性能，避免模型过度拟合。在UCI标准数据集和烟叶综合质量评价数据中应用改进的LMT算法进行建模验证，结果表明，该改进方法在模型精度和召回率方面基本优于其他决策树方法，时间性能比改进前提升50%左右，能较好地评价烟叶综合质量。

　　关键词： 逻辑模型树；UCI标准数据集；烟叶综合质量评价数据；赤池信息量准则；模型精度；召回率

0 引言

　　决策树分类法是一种简单而广泛使用的分类技术，是数据挖掘分类算法的一个重要方法，可以用于分析数据，同样也可以用作预测。决策树法作为一种决策技术，已被广泛地应用于企业的投资决策之中，它是随机决策模型中最常见、最普及的一种规策模式和方法，能有效地控制决策带来的风险[1]。决策树易于理解和实现，能同时处理数据型和常规属性，能够在相对短的时间内对大型数据源做出可行且效果良好的结果[2]。线性逻辑回归和树归纳是两种常用的决策树分类方法。但线性逻辑回归在拟合简单模型时会导致低方差和高偏差；而树归纳会导致低偏差和高方差[3]。因此，将两种分类方法相结合，提出逻辑模型树方法，不仅能分类，而且能得到类概率估计, 能够直接体现数据的特点，并且参数少，应用方便，模型准确度较高。

　　鉴于LMT算法的以上优点，研究将其应用在烟草企业烟叶综合质量评价中。目前，在烟草企业中，烟叶的质量主要根据化学成分值和评吸专家的评吸来综合判定。在判定过程中，各位专家要经过反复讨论来判定每种烟叶的质量层次，以便烟草原料研究人员在配方使用前对烟叶进行初步筛选。为减少烟叶质量层次判定的讨论时间，本文利用改进的LMT算法对烟叶数据进行建模并预测烟叶的质量层次。在实际应用中，提高了烟草原料研究人员的工作效率。

　　1 LMT算法基本原理

　　1.1 LMT简介

　　LMT算法是由Niels Landwehr、Mark Hall 和 Eibe Frank在2003年第十四届关于机器学习欧洲会议上提出的[4]。逻辑模型树是由叶子上带有逻辑回归函数的标准决策树结构构成的。这个方法采用LogitBoost算法在树的节点上建立逻辑回归函数[5]，并使用CART算法进行剪枝[6]。本文利用AIC准则改进LMT算法[7]，以减少决策树的逻辑回归模型的计算复杂度，从而减少训练时间。

　　1.2 LogitBoost算法

　　Logitboost算法是改进的Boosting算法。其基本思想是：基于现有样本数据集构建一个基础的“弱分类器”，反复调用该“弱分类器”，通过对每轮中错判的样本赋予更大的权重，使其更关注那些难判的样本，经过多轮循环，最后采用加权的方法将各轮的“弱分类器”合成“强分类器”，从而得到较高精度的预测模型[8]。

　　1.3 CART算法

　　CART算法选择具有最小基尼指数值的属性作为测试属性， 并采用一种二分递归分割技术， 将当前样本集分为两个子样本集， 使得生成的决策树的每一个非叶节点都有两个分枝。最后生成的决策树是结构简洁的二叉树，用独立的验证数据集对训练集生长的树进行剪枝，不易产生数据碎片。CART剪枝算法使用独立于训练样本集的测试样本集对子树的分类错误进行计算， 找出分类错误最小的子树作为最终的分类模型[9]。

　　1.4 LMT算法步骤

　　LMT算法步骤描述如下：

　　⑴ 建立根节点；

　　⑵ 建立逻辑模型树：

　　① 初始化

　　权重Wij=1/n,i=1,…,n,j=1,…,J

　　分类器Fj(x)=0；概率估计pj(x)=1/J

　　② 利用五折交叉验证得到最佳迭代次数M

　　③ 进行迭代， m=1,…,M

　　a.分别计算作业应变量和权重

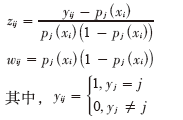
　　b.采用加权最小二乘法拟合弱分类器函数fmj(X) ：

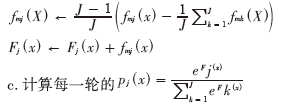
　　c.计算每一轮的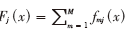

　　④ 输出最终的分类器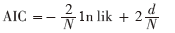，根据正负对样品判别归类；

　　⑶ 继续分裂样本，并对分裂样本的数据子集再重复步骤⑵建树，直至停止分裂；

　　⑷ 利用CART算法对其进行修剪。

　　1.5 AIC准则

　　本研究中使用泛化误差的样本内估计赤池信息量准则来替换原算法中交叉验证选取最佳迭代次数来改进LMT算法[10]。赤池信息量准则（Akaike Information Criterion），又称为AIC准则。赤池建议，当欲从一组可供选择的模型中选择一个最佳模型时，可选择AIC为最小的模型。赤池信息量准则的方法是寻找可以最好地解释数据但包含最少自由参数的模型[11]。

　　AIC提供了当使用可能性损失函数时的泛化误差估计，其定义为：

　　missing image file

　　其中，d是迭代次数，lik为模型的极大似然函数，N是训练实例个数。随着d的增长，等式的第一项下降（因为LogitBoost完成拟牛顿算法，接近最大似然函数对数），第二项总是会增加。因此，选最佳迭代次数是最小化AIC时的迭代次数d。

　　使用AIC标准来防止模型过度拟合，训练时间比原LMT算法快很多[7]。研究中默认AIC最小迭代是50次。

2 实验分析

　　2.1 分析环境

　　研究利用Weka软件对数据进行建模。Weka的全名是怀卡托智能分析环境，是一款免费的、非商业化的、基于JAVA环境的开源机器学习以及数据挖掘软件。Weka作为一个公开的数据挖掘工作平台，集合了大量能承担数据挖掘任务的机器学习算法，包括对数据进行预处理、分类、回归、聚类、关联规则以及在新的交互式界面上的可视化[12]。

　　2.2 数据描述

　　UCI标准数据集：UCI数据库是加州大学欧文分校提出的用于机器学习的数据库，这个数据库目前共有187个数据集，其数目还在不断增加，UCI数据集是一个常用的标准测试数据集，从中挑选iris、segment、glass三个标准数据集进行建模预测。

　　烟叶数据：该烟叶实验数据由全国各省不同等级的入库烟叶组成，包括产地、等级、质量层次、各化学成分值和各感官评价分数等，其中质量层次数据是各位专家根据经验和评吸情况通过共同讨论综合决定的。实验中，训练建模数据选择全国各省数据355条，测试数据分别选择云南省上部烟数据16条、云南省中部烟数据28条。

　　2.3 实验步骤

　　针对UCI标准数据集，分别用LMT算法及其他决策树对比算法建模，对结果进行比较分析，然后用改进的LMT算法对数据集进行建模，与原LMT算法结果进行对比分析。

　　针对烟叶数据，首先剔除含有缺失值的烟叶，然后对输出属性数据即质量层次数据进行离散化，由于有多种描述烟叶各方面的指标，本研究通过特征指标选择，选取施木克值、总糖、杂气、香气质、余味、香气量、刺激性、湿润程度作为建模特征指标数据，最后利用改进的LMT算法对其建模预测，并分析结果。

　　2.4 实验验证

　　实验一：不同的算法在UCI标准数据集中的结果

　　取iris、segment、glass 3个不同的标准数据集，数据集的信息如表1所示。对3个标准数据集分别用LMT、Logistic、J48、NBTree 4种算法进行建模分类，其性能结果分别如表2、表3、表4所示。

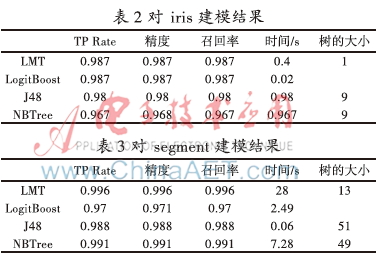
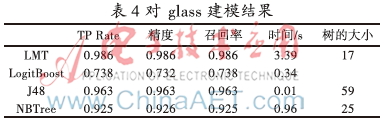
　　从表2、表3、表4中可以看出，LMT算法的TP Rate、精度、召回率均比LogitBoost、J48、NBTree算法高，而且LMT建模的树规模最小，说明LMT算法在保证建模准确率的前提下，通过逻辑模型使树更易被解释，但缺点是由于计算复杂度高导致耗时过长。针对这一问题，利用AIC准则对LMT算法改进，提高时间性能。

　　实验二： AIC准则对LMT算法的影响

　　针对3个UCI标准数据集，使用AIC准则和不使用AIC准则分别进行建模，其性能结果如表5所示。

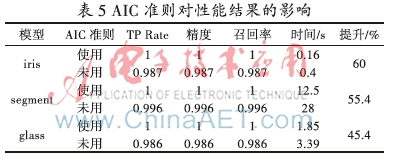
　　从表5中可以看出，使用AIC准则后，对3个数据集进行建模，TP Rate、精度、召回率、时间性能均有不同幅度的提升，说明使用AIC准则可以对LMT算法进行有效的改进。

　　实验三：利用改进的LMT算法对烟叶数据进行建模预测

　　先用NBTree算法对355条全国各省不同等级烟叶的化学成分数据和评吸质量分数来建模，模型的精度和时间性能结果并不理想。再用改进的LMT算法对烟叶数据建模，然后利用模型分别将16条云南省上部烟数据、28条云南省中部烟数据对各烟叶的质量层次进行预测，其结果如表6所示。

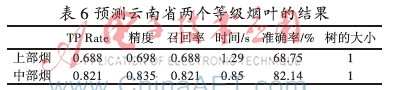
　　从表6中可以看出，改进的LMT算法对云南省的两个部位的烟叶预测结果较为理想。由于质量层次数据是由专家讨论综合决定，存在一定的人为因素，所以准确率较标准数据集略低，但在实际应用中，该算法建模预测能较好地评价烟叶综合质量。因为中部烟数据量多，建立的模型更加完备，因此预测较上部烟更为准确。

3 结束语

　　本文介绍了LMT算法的基本原理，针对LMT算法的时间性能问题，利用AIC准则通过改进选取最佳迭代次数的方式，使时间性能大幅度提升。通过对比LMT算法与其他算法对标准数据集建模的结果发现，LMT算法在模型精度上优于其他算法，模型精度高，结果易于解释，并且改进的LMT算法使时间性能提升50%左右。使用改进的LMT算法对烟叶数据建模预测，结果表明改进的LMT算法对模型的准确率有相应的提高，而且能够有效地提高时间性能。实验表明改进的LMT算法较其他算法更适用于评价烟叶综合质量。该模型在企业实际应用的结果表明，可以在入库片烟质量评价过程中快速、有效地依据化学成分和感官指标判定烟叶的综合质量，减少专家评吸次数，并且为原料在不同档次卷烟配方中的可用性提供信息支撑。

参考文献

　　[1] 田苗苗. 数据挖掘之决策树方法概述[J]. 长春大学学报, 2005,14(6): 48-51.

　　[2] 陈诚. 基于AFS理论的模糊分类器设计[D]. 大连:大连理工大学, 2009.

　　[3] Perlich C, Provost F, Simonoff J S. Tree induction vs. logistic regression: a learning-curve analysis[J]. The Journal of Machine Learning Research, 2003, (4): 211-255.

　　[4] Landwehr N, Hall M, Frank E. Logistic model trees[J]. Machine Learning, 2005, 59(1/2):161-205.

　　[5] Friedman J, Hastie T, Tibshirani R. Special invited paper. additive logistic regression: A statistical view of boosting[J]. Annals of statistics, 2000,28(2): 337-374.

　　[6] Breiman L, Friedman H, Olshen J A. Classification and Regression Trees[M]. New York:Wadsworth,1984.

　　[7] Sumner M, Frank E, Hall M. Speeding up logistic model tree induction[M].Knowledge Discovery in Databases: PKDD 2005, Springer Berlin Heidelberg, 2005.

　　[8] 富春枫,荀鹏程,赵杨,等. logitboost 及其在判别分析中的应用[J]. 中国卫生统计, 2006,23(2):98-100.

　　[9] 季桂树,陈沛玲,宋航. 决策树分类算法研究综述[J]. 科技广场, 2007(1):9-12.

　　[10] Akaike H. Information theory and an extension of the maximum likelihood principle[M].Breakthroughs in statistics, Springer New York, 1992.

　　[11] De Ridder F, Pintelon R, Schoukens J, et al. Modified AIC and MDL model selection criteria for short data records[J]. Instrumentation and Measurement, IEEE Transactions on, 2005, 54(1): 144-150.

　　[12] 陆远蓉. 使用数据挖掘工具Weka[J]. 电脑知识与技术, 2008,1(6):988-993.