0 引言

　　在无线通信系统、高清电视以及其他领域，宽带低功耗ΣΔ模数转换器越来越受到人们的欢迎[1]。对于无线窄带的中频无线通信系统，带通的ΣΔ调制器是高精度A/D转换器的最佳选择[2]。目前关于ΣΔ带通调制器的研究工作大多数都是集中于传统结构，然而低失真结构能够实现更优越的性能。因为低失真结构采用一个信号前馈通路，使得谐振器只处理量化噪声，这样就能获得更高的线性度。另外低失真结构对于谐振器的非线性较传统结构而言也不敏感[3]。在调制器电路中采用双采样技术能够有效地增加系统的过采样率（OSR），同时并不增加时钟频率，这样能够降低对运算放大器建立时间的要求。目前关于低失真结构的低通调制器的研究工作开展较多，而对中频带通调制器而言，报道低失真结构的文献还较少。低失真的带通ΣΔ调制器结构首先在参考文献[3]中被提出来，但是其并没有给出其具体实现方式；参考文献[4]对这种低失真结构进行了研究，但是并没有对其非理想因素进行分析。本文基于一种双采样双延迟谐振器，提出一种低失真中频带通sigma-delta调制器电路，分析了其非理想特性并在MATLAB的Simulink里进行建模。通过对比行为级模型仿真结果和电路的后仿真结果，验证了所建立模型的准确性。本文也对带通调制器的稳定性进行了分析，并给出了电路图和版图后仿真结果。

1 主要非理想特性分析

　　1.1 模拟开关热噪声和非线性

　　模拟开关在导通时会形成一个导通电阻，这个导通电阻将会产生热噪声，且会被开关电容电路采样到采样电容上，对输出信号产生影响。当开关的导通电阻为Ron时，模拟开关的噪声功率可以表示为[5]：

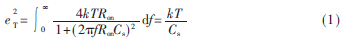
　　式中，Cs为采样电容值，k为波耳兹曼常数，T为绝对温度。其非理想模型如图1所示。

　　1.2 运放热噪声

　　在调制器系统中，运算放大器的噪声是系统的主要噪声来源之一。不同于低通调制器的低频应用，中频调制器可以不考虑运放的1/f噪声对系统的影响。常见的运放热噪声模型如图2所示。

　　1.3 谐振器非理想模型

　　谐振器的非理想特性主要由运放的有限直流增益、运放有限增益带宽、寄生电容等因素引起。本设计的谐振器非理想传输函数可以用下式表示[6]：

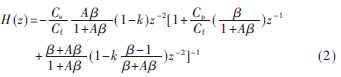
　　其中，Cs为谐振器的采样电容，Cf为谐振器的积分电容，Cp为运放的输入端寄生电容，A为运放的直流增益，为反馈系数，k为运放的有限增益带宽引起的非理想因子。图3的非理想谐振器模型中包含了上述的非理想因素。

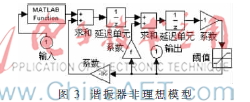
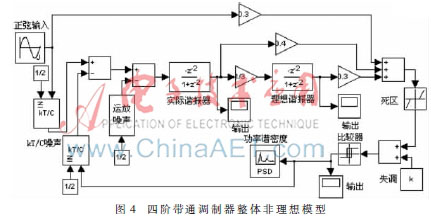
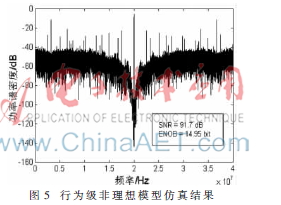
　　基于低失真带通调制器的结构和上面分析的主要非理想特性，建立图4中的调制器整体行为级模型，其中还包含了量化器的失调和死区特性，以便更准确地模拟中频带通调制器的行为，为后续设计提供指导。当采样频率为80 MHz、输入信号20 MHz、信号幅度为-0.915 dBFS时，行为级仿真结果如图5所示，显示该调制器实现了91.7 dB的信噪比(SNR)。

　　2 稳定性分析

　　在较低的过采样率的情况下，如果提高调制器的阶数，相对而言能够获得较高的SNR。但是在实际设计中，高阶的调制器系统会存在稳定性问题。由于量化器的增益是随输入信号变化的，所以调制器实际上是一种非线性系统。图6是准线性的调制器模型，其中量化器的增益k随着输入信号幅度变化而变化，这样量化器输出就等效成一个随输入信号可变的因子与量化噪声之和。

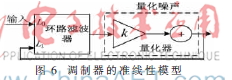
　　图4中的带通调制器的反馈环路函数如式(3)所示，因此可以写出准线性模型下的量化噪声传输函数，如式(4)所示：

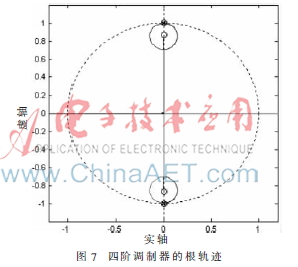
　　由于量化器的增益是随着输入信号幅度的变化而变化的，所以量化器增益的变化会改变系统噪声传输函数的极点的位置。对于稳定的系统，极点必须在单位圆内部。分析系统的根轨迹一般被用来作为判定系统稳定性的一种手段，可以在MATLAB中求出该带通调制器的NTF的根轨迹，如图7所示。当k值增大时极点会从实轴上往单位圆外移动，如上文所述，调制器能恢复稳定状态；当k值减小时，极点始终处于单位圆内。因此可以看出，本设计的带通调制器是无条件稳定的。

3 电路设计和版图后仿真

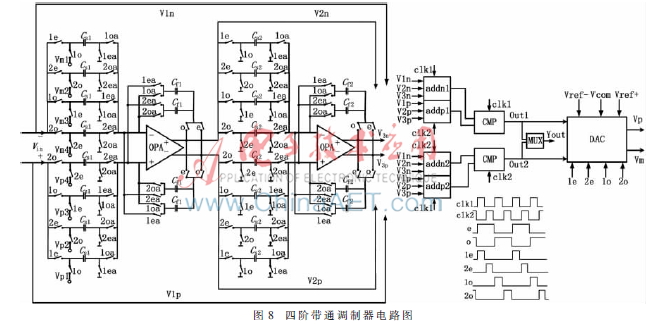
　　图8中是基于一个双采样技术的全差分四阶带通ΣΔ调制器电路。该电路由两级谐振器、两路求和电路、两路比较器以及一位DAC等组成。图4中的前级比例系数由谐振器的采样电容值和积分电容值的比值确定，后级系数由求和电路的电容比例确定。该调制器电路的等效采样时钟频率是信号频率的4倍。谐振器电路在clk1高电平和clk2的高电平分别进行采样和积分。在4项时钟1e、2e、1o、2o控制下，实现了两个采样周期的延迟，同时实现了两次采样。

　　由于谐振器在clk1和clk2都进行采样和积分，故降低了一半的采样频率，而等效采样频率不变。这样对谐振器电路的建立时间要求就降低了很多，降低了对运放的带宽要求。另外谐振器的输出摆幅可以通过改变采样电容和积分电容值的大小来降低，这虽然降低了系统的线性度，但是可以进一步降低系统的功耗。该调制器电路的采样电容引入的kT/C噪声是系统的主要噪声来源。为避免量化误差，同时考虑到运放负载对功耗和速度的影响，取CS1=0.8 pF。由于后级电路的噪声可以通过前级抑制，所以第二级谐振器的采样电容可以大大减小，取CS2=0.2 pF，因此第二级谐振器的负载电容大大减小，功耗得到优化。谐振器的积分电容可以根据行为级确定的比例系数来确定。求和电路采用常见的无源开关电容求和电路来实现，以降低芯片面积，减小功耗。求和电容分别为0.3 pF、0.4 pF、0.3 pF。两路求和电路的输出分别送给比较器电路，最后由选择器将两路位流合并为一路输出。

　　在TSMC 0.18 m工艺下对该全差分调制器电路进行版图设计。该调制器工作在80 MHz的等效采样频率下，当输入信号频率20 MHz、幅度约为-0.915 dBFS时，其输出位流在MATLAB里经过计算绘制的频谱图和信号带宽内细节图如图9所示，SNR为85.5 dB。版图的后仿真包含了运放的有限增益带宽、非理想开关、寄生效应、建立误差等非理想效应，其结果与行为级建模相比，SNR下降了约6 dB。这可能是由于版图的不对称和工艺误差导致的，但版图的后仿真结果和行为级建模仿真结果基本一致，可以看出前文对调制器的非理想特性进行的行为级建模的准确性和有效性。通过改变输入信号幅度，得到的调制器动态范围（DR）如图10所示，从图中可以看出，该调制器在大信号和小信号激励下都具有良好的稳定性。当输入信号幅度增大到一定范围，谐振器开始过载，输出谐波失真分量增加。另外谐振器输出过载也导致了谐振器的传输特性发生变化，从而导致整个调制器的信号传输函数发生改变，这些都会降低系统的线性度。从图10中可以看出系统的DR约为87 dB。

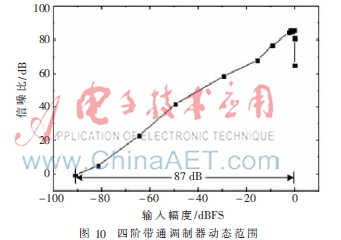
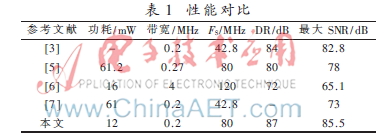
　　表1将本文的带通调制器性能与参考文献中的进行了比较，可见本文设计的调制器电路具有功耗低、动态范围大、信噪比高的特点，适合于高性能低功耗的通信系统应用。

4 结论

　　本文对一个四阶带通ΣΔ调制器的非理想特性进行了分析并进行了建模，利用根轨迹法对调制器系统的稳定性做了分析。在TSMC 0.18 ?滋m工艺下完成了电路和版图设计，通过对比版图的后仿真结果和调制器的行为级非理想特性建模结果可以发现性能基本一致，说明了建立的行为级非理想模型的准确性和所设计电路功能的正确性。

参考文献

　　[1] 邓玉清，唐宁，曹杰.高精度音频Σ-Δ DAC的设计[J].电视技术，2011，35(7)：56-58.

　　[2] WAKI N，SATO H，HYOGO A，et al.A low-distortion two-path fourth-order bandpass delta-sigma modulator using horizontal opamp sharing[C].50th Midwest Symposiumon Circuits and Systems，2007：1372-1375.

　　[3] RUSU A，ISMAIL M.Low-distortion bandpass Σ-Δ modula-tor for wireless radio receivers[J].Electronical Letters，2005，41(19)：1044-1046.

　　[4] XU H L，LIU X W，HUANG F X，et al.Low-distortion bandpass ΣΔ modulator using two-path double-sampling technique[J].IEICE Electronics Express，2014，11(12)：1-6.

　　[5] SUAREZ G，JIMENEZ M，FERNANDEZ F O.Behavioral modeling methods for switched-capacitor ΣΔ modulators[J].IEEE Trans. on Circuits and Systems，2007，54(6)：1236-1244.

　　[6] TEMES G C.Finite amplifier gain and bandwidth effects in switched-capacitor filters[J].IEEE Journal of Solid-State Circuits，1980，15(3)：358-361.

　　[7] 陈凯，张文俊，余志平.Σ-Δ调制器的非理想特性建模与验证[J].微电子学与计算机，2010，27(5)：5-8.