0 引言

　　电源设计中整流桥电解电容器的选择一般是根据允许的纹波电压和电流来选取[1]。纹波电流主要影响的是其流过电容器的等效串联电阻（ESR），产生功耗，使电容器发热，影响使用寿命。这个功耗的大小与纹波电流成正比关系[2]。在选择中，容值的不同会引起其纹波电流的不同及纹波承受能力的不同。但是人们往往忽略了电压波动和闪变对电容纹波电流的影响，或是考虑到此，又预留过大的容限造成浪费。

　　电网电压波动和闪变对整流桥后电解电容器的纹波电流大小存在影响[3]。分析这一影响，有利于电解电容器的选择，使其不至于因预留过大的纹波电流承受容限造成较高的成本，也不至于因容限过小使使用寿命大打折扣。

1 电压波动和闪变

　　在电能质量研究中，闪变是用来描述电压波动的现象[4-5]。它源于白炽灯受电压波动的影响而引起能够被人感知的闪烁。对电压闪变的研究，人们通常比较关注人感知比较敏感的频率段——0.5 Hz~35 Hz。

　　图1为闪变研究中引起电压幅值变化的电压波动实例[6]。标准正弦波经过调制波调制后会产生除基波外的上边频和下边频[7]，且在整流桥电路中会反映在电容纹波电流上。

2 电解电容器的波形描述及特点

　　图2所示为正常电网电压输入时，电容器稳定状态的电压电流波形。vc为电容的电压波形，ic为电流波形（输入为正，输出为负）。图3所示为输入电压波动和闪变经过整流桥后的波形。假定输入函数为：

　　其中V是不规则的。调制信号Vsint是根据GB/T 12325-2008和IEC_60038-2009标准，幅值为标准电压的

　　±10%和频率为0.5 Hz~35 Hz，且在这范围内是不规则，图1为一例子。那么，由于电压的波动，图2所示的稳态将不复存在，电容器的导通角也发生了变化，如图3所示，其比稳态状态下大或者小，甚至某半周不导通。如此，电容器的充放电电流与稳态状态不同。如前所述，由于标准电压上叠加一个调制信号，电容输入电流就带有调制频率的各次谐波。所以，电容的纹波电流将发生变化，充电时脉冲振幅可能出现过高或过低的值，导致充电电流有效值不同；又因负载相同，放电电流大小基本不变[8]。这些现象在实测中都可以测得波形。

3 纹波电流的理论分析与推导

　　为了比较两种情况下纹波电流特征，在推导过程中，假定（1）电容充电电流波形为相似三角形，且每个周期都是一样的，如图2、图3中的电流波形虚线三角形是相似的；（2）电容放电电流大小（Idis）不变，即负载保持不变；（3）整流二极管为理想的二极管。

　　图2中Ipeak_a为电容半周充电电流峰值，ta为半周充电时间。假设稳态时间为T，期间电容充电Qchg_a，充电电流有效值是Ichg_rms_a；放电Qdis_a，放电电流有效值是Idis_rms_a；总电流有效值是IT_rms_a。那么：

　　在此，稳定状态下Qchg_a=Qdis_a，放电电流Idis_a保持不变。

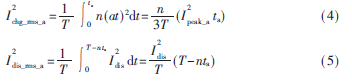
　　则：

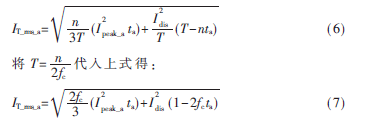
　　同样，图3中Ipeak_b为输入电压异常时电容半周充电电流峰值， tb为半周充电时间。在周期T下，电容总充电Qchg_b，充电电流有效值是Ichg_rms_b；总放电Qdis_b，放电电流有效值是Idis_rms_b；总电流有效值是IT_rms_b。

　　下面用反证法证明Qchg_b>Qchg_a，Qdis_b>Qdis_a。由假定(1)可以得到：

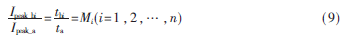
　　其中Mi为相似系数。

　　假设1：

　　Qchg_b<Qchg_a

　　Qdis_b<Qdis_a(10)

　　结合式（3）、式（8），将式（9）代入式（10）得：

　　Mi为正实数，n为正整数。很明显，式（11）是不成立的，假设1不成立；

　　假设2：

　　Qchg_b=Qchg_a

　　Qdis_b=Qdis_a(12)

　　结合式（3）、式（8），将等式（9）代入（12）得：

　　根据拉格朗日乘数法，当且仅当Mi的值相同时，式（13）成立。这意味着电容充电电流的波形需要一致，而其实在电压波动和闪变的条件下充电电流波形是不规则的，所以假设2不成立；

　　假设3：

　　结合式（3）、式（8），将等式（9）代入（14）得：

　　在Mi为正实数和n为正整数的条件下，式（15）是成立的，证毕。

　　因此，由式（3）、式（8）和式（14）得：

　　最后将计算电压波动和闪变情况下电容纹波电流有效值，并和在正常电压情况下作比较。

　　由式（16）、式（17）、式（21）以及式（7）得到IT_rms_b>IT_rms_a。

　　以上分析表明在正常电压输入的情况下电容充放电电流有效值都比电压异常情况下的有效值小。当电压波动时，充电电流需要在较短时间内得到足够的电能导致充电电流有效值加大；而放电电流的有效值加大是由于放电电流大小不变，但放电时间变长了。所以，电容器的纹波电流有效值在电压波动时会明显地变大。这个结论也将在第四部分实试中得到验证。

4 电解电容器纹波电流的测试方法与实验

　　4.1 测试方法说明

　　实际电路中，纹波电流含有各频率波形的纹波电流，所以对实际纹波电流的计算应由纹波电流Irms得到。通常结合纹波电流(if)和其相应频率系数(kf)将纹波电流归一化在120 Hz频率下：

　　在测试时，输出负载不变，因此电容的放电电流在正常输入电压下是一致的。现将电网电压波动和闪变时整流桥电解电容器充电电流的120 Hz以下各频率分量和120 Hz及以上的频率分量分离出来，并将其各自归一化成120 Hz的分量，求均方根。再将此归一化成120 Hz的电流与正常输入电压下的归一化成120 Hz的低频充电电流做比较，得电压异常对其纹波电流的影响。

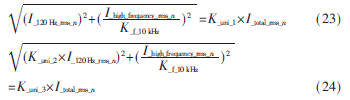
　　其中，在正常电压下，I_120 Hz_rms_n为充电交流有效值；I_high_frequency_rms_n为高频放电交流有效值；I_total_rms_n为总电流有效值；K_f_10 kHz为10 kHz频率点的频率系数。K_uni_1为归一化成120 Hz的纹波电流与I_total_rms_n的比例系数；K_uni_2为电压波动时电容归一化的充电电流与I_120 Hz_rms_n的比例系数；K_uni_3为电压波动时归一化的纹波电流与I_total_rms_n的比例系数；K_uni_increase为电压波动时归一化纹波电流与正常电压时的比例系数。

　　由式（23）、式（24）得：

　　从表达式知，只要得到不同条件下的K_uni_1、及K_uni_2就可求得相应的K_uni_increase。

　　4.2 实验测试

　　实验测试的电解电容器为一样机上的铝电解电容器。该样机有三组输出电压，且负载不变，输出为5 V/2.76 A、12 V/1.69 A、24 V/1.13 A，输入功率为74.5 W。

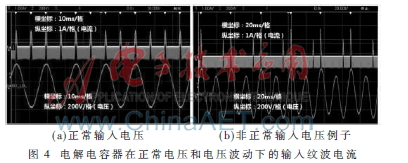
　　图4(b)为电压波动和闪变时电容的输入电流。很明显，验证了第三部分所述的存在或高或低的充电电流，甚至某半周无充电的现象。对于测量输入纹波电流的低频部分是利用带有傅里叶分析功能的示波器测得，如图5所示。图中低频纹波电流的频率不是单纯的线电压频率和各次谐波而是还包含调制波带来的多频率分量。

　　在实验测试中，利用变频器输出标准电网电压和模拟电压波动和闪变。电压波动和闪变为标准电网电压幅值的5%~15%，频率为5 Hz~30 Hz。

　　表1是220 V/50 Hz输入时，电压波动和闪变的电容输出电流，值基本不变，与之前描述一致。

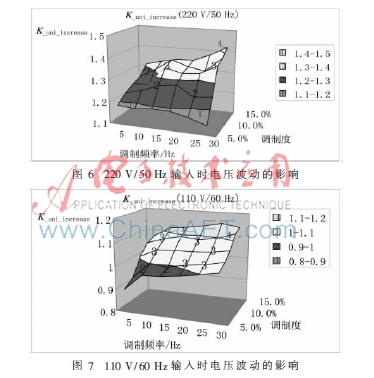
　　图6、图7为标准电压为220 V/50 Hz和110 V/60 Hz条件下测得的。可以看出，调制信号幅值波动和频率变化会使电容输入纹波电流有效值发生变化。随着调制幅度和频率的增加，电容器输入纹波电流有效值也相应增加。特别地，在调制度较高时，电流有效值增速相对较为激烈，在这种情况下，电容器出现不良的概率也更高。但是比较不同的输入标准电压，电压波动和闪变对于220 V/50 Hz的输入影响比较大，最高超过正常输入的1.4倍以上。

5 结论

　　本文通过三角函数模型定性地分析了电压波动和闪变引起整流桥后电解电容器纹波电流的变化，以及理论推导得出其包括充电电流有效值、放电电流有效值和总纹波电流有效值比在正常电压输入时大。最后，本文给出纹波电流的测试方法，同时实验测得在负载不变时，电压波动和闪变对单向整流桥电解电容器纹波电流的影响。实验表明，整流桥电解电容器的充电电流有效值随着调制信号幅度和频率的增加而增加，从而其纹波电流有效值增加。因纹波电流有效值增加会引起电容器的耗散功率加大，其本体温度上升可能导致使用寿命的减短。所以，实验结论可供有考虑电网电压波动和闪变时整流桥电解电容器的选型做参考。

参考文献

　　[1] 徐立刚，陈乾宏，朱祥，等.整流后滤波用电解电容的选择[J].元器件运用，2008(10)：69-73.

　　[2] AMARAL A，CARDOSO A.An economic offline technique for estimating the equivalent circuit of aluminum electrolyticcapacitors[J].IEEE Trans.Instrum.Meas，2008，57(12)：2697-2710.

　　[3] REDL R.Electromagnetic environmental impact of power electronics equipment[J].Proc.IEEE，2001，89(6)：926-938.

　　[4] 林海雪.电压波动和闪变标准[J].建筑电气，2011(8)：444-448.

　　[5] CAI R，COBBEN J，MYRZIK J，et al.Flicker responses of different lamp types[J].IET Generation，Transmiss.Distrib，2009，3(9)：816-824.

　　[6] Electromagnetic compatibility(EMC)-part 4-15：Testing andmeasurement techniques-flickermeter-function and design specifications，IEC 61000-4-15，edition 2.0(2010-08) Std[Z].2010.

　　[7] 曾兴雯，刘乃安，陈健.高频电子线路[M].北京：高等教育出版社，2005.

　　[8] GANDOY J D，CASTRO C，MARTINEZ M.Line input ac-to-dc conversion and filter capacitor design[J].IEEE Trans.Ind.Appl，2003，39(4)：1169-1176.