0 引言

　　以短距离无线通信为基础的无线传感网(WSN)和无线体域网(WBAN)的飞速发展给人们的生活带来了巨大的影响，无线数据采集网络正广泛应用于交通、安全、医疗等各个领域。无线节点和移动终端具有体积小、计算能力受限、电源能量有限等特点。为了避免频繁更换电池，低功耗设计成为了一个基本要求[1]。目前无线节点和移动终端的上行链路大多采用BPSK或者QPSK等低阶调制方式。在短距离无线通信中采用高阶调制有助于提高传输能效，但由于高阶调制对功放的非线性失真较为敏感，且在发射端校准失真需要消耗更多额外功耗，因此需要采用其他解调性能更优的算法。

　　目前云无线接入网(Cloud Radio Access Network，C-RAN)架构正在逐步兴起[2]，并得到了运营商的大力支持，如日本NTT、法国电信、西班牙电信和中国移动等。如图1所示为微单元C-RAN架构[2]，覆盖范围较小的无线接入单元（RAU）替代了传统的基站，RAU接收无线终端的射频信号，并直接将频带信号通过RoF链路传输至基站池统一处理。基站池充足和强大的计算资源为使用K-means算法的实现提供了保证。

1 相关工作

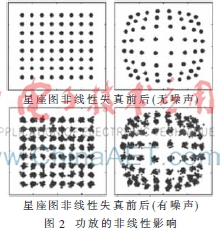
　　功率放大器是无线通信系统中耗能较多的模块，其非线性效应将使QAM星座图“外聚内散”，如图2所示。为减小功放的非线性影响，传统方法把输入功率从1 dB压缩点向后回退，尽量使用线性放大区，这将导致功放的电源利用率降低。之后人们提出一系列的功放线性化技术，如前馈技术、LINC技术、预失真技术等，这些方法都将不同程度地增加发送端电路的复杂度。以目前主流的数字预失真技术[3]为例，预失真模块通常需要复杂的数字信号处理电路来完成，并不适用于计算能力和功耗严格受限的无线数据采集节点和移动终端。

　　目前将K-means算法用于解调的相关研究较少，参考文献[4]中使用K-means算法实现了波分复用系统的QPSK相干检测，参考文献[5]通过K-means算法实现了8PSK的相位恢复，这两篇文献均只将K-means算法用于光纤通信中低阶调制的解调。由于目前K-means算法主要应用于数据挖掘、模式识别等领域，如何将其移植到通信场景的高阶解调中是本文讨论的重点。

2 算法分析与改进

　　2.1 K-means解调分析

　　K-means解调的关键是将传统解调中的多电平判决改为K-means聚类判决，因此K-means并不是对单个符号进行判决，而是接收到一帧或多帧数据后，同时对若干符号一起进行聚类后再判决。关键步骤有两步：(1)对所有点进行聚类，将接收机经过相干解调、滤波和定时抽样得到的若干数据点聚为K簇，K为调制阶数；(2)判决每一簇的星座编号。QAM调制中对星座图的编号一般从左下点到右上点连续编号，这使得第(2)步判决编号对第(1)步的聚类结果相当敏感，一个星座只能对应一簇聚类结果。“两星座一簇”或“一星座两簇”都会影响之后其他簇的编号，从而出现大面积的星座编号判决错误。目前对K-means算法的改进研究较多，如Heuristic K-means改进算法[6]、KMTR改进算法[7]、基于KD树改进算法[8]等。这些改进算法都是在未知任何数据信息的情况下进行聚类，然而通信中可利用某些先验信息对算法进行改进，将提高算法的稳定性，降低错误概率。

　　2.2 K-means算法改进

　　以矩形星座为例，本文提出的初始聚类中心选取算法的基本思想为：首先估算数据点分布的整个星座区域的范围，再对四边形区域进行非均匀网格划分，得到M×M个网格点，即M行M列，然后与理想星座图对比去除无关点，最后将剩下的点分别更新为距离最近的数据点，并按星座编号的方法进行编号，即得初始聚类中心，其中M是矩形星座的行数或列数。如图3所示，以32QAM为例显示了算法的中间结果，算法得到的初始聚类中心能达到“一簇一心”良好效果。算法的伪代码描述如下：

　　输入：数据点横坐标集X{x1，x2，…，xn}，纵坐标集Y{y1，y2，…，yn}，QAM调制的阶数K，矩形星座行数M，非均匀划分系数ceta。

　　输出：K个初始聚类中心点C1，C2，…，Ck

　　//step1 估算四边形区域

　　for i=1:n

　　if [x(i),y(i)]rth quadrant (r = 1,2,3,4)

　　xr(i) = x(i);

　　yr(i) = y(i);

　　end

　　end

　　for r=1:4

　　mxr = max(xri);

　　myr = max(yri);

　　end

　　P1= (mx3,my3);

　　PM= (mx4,my4);

　　PM×M=(mx1,my1);

　　PM(M-1)+1=(mx2,my2);

　　// step2 非均匀网格划分

　　Div_n_part(P1, PM(M-1)+1, M, 0.2 );

　　Div_n_part(PM, PM×M, M, 0.2 );

　　for i=0:M-1

　　Div_n_part( PM*i+1, PM*(i+1), M, 0.2 );

　　end

　　// step3 比对去点并编号

　　for j=1:M2

　　if Pj  Constellation

　　for i=1:n

　　if min(d(xi,Pj))=d(xi,Pj)

　　Ci=xi;

　　end

　　end

　　//非均匀划分函数，将线段P1Pn划分为n-1段

　　function [P2,P3,…,Pn-1] = Div_n_part(P1, Pn, n, ceta)

　　Eq_dist = (Pn-P1)/(n-1);

　　Neq_dist(n/2)=[(Pn-P1)+ceta*(Pn-P1)4*(n-2)/4]/(n-1);

　　for i=1:n/2

　　Neq_dist(n/2+1-i)=Neq_dist(n/2)–i*Eq_dist*ceta;

　　Neq_dist(n/2+1+i) = Neq_dist(n/2+1-i);

　　end

　　for i=1:n-1

　　Pi+1=Pi+Neq_dist(i);

　　end

　　end

3 结果分析

　　3.1 算法复杂度分析

　　表1例举了3种近年来针对初始化聚类中心的改进算法，可以看出本文提出的改进算法时间复杂度较低，更适合应用于通信接收机中以降低接收延时。列表参数说明：n为数据集中数据的个数，K为聚类的类数，Ts为算法迭代次数，beta为KD树划分终止系数。

　　3.2 解调性能对比分析

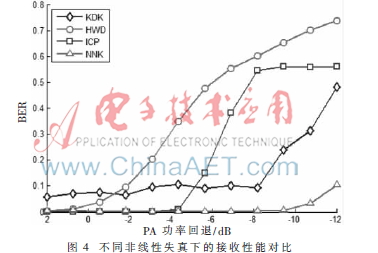
　　本文以64QAM为例，分别对基于KD树的K-means算法（KDK）[8]、传统硬判决法（HWD）、以理想星座为初始质心的K-means算法（ICP）[4-5]、本文改进算法（NNK）进行了仿真比对。如图4所示，Eb/N0=7 dB，横坐标为输入功率距P1dB的回退位置（PBF）。功放失真模型采用基于反正切函数的非线性模型[9]。从接收性能曲线可以看出，传统硬判决算法功放输入功率应比P1dB小1 dB，本文改进的算法可比P1dB大9 dB左右。

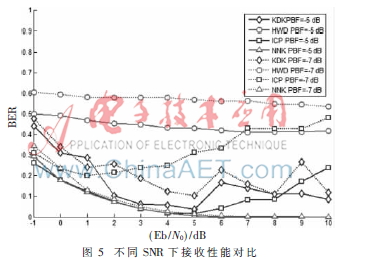
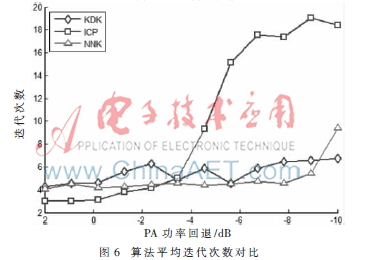
　　图5所示为不同解调算法的性能对比，本文提出的改进算法解调性能更稳定，接收错误率较低。图6所示为算法平均迭代次数的对比，可以看出本文改进算法平均迭代次数较低，算法可以快速收敛。

4 结论

　　K-means聚类算法是数据挖掘等领域著名的无监督学习算法，本文基于通信场景中的先验信息，将其改进为半监督学习算法并应用于QAM解调中。虽然较传统方法步骤更加复杂，但性能更优，使在特定通信场合中以“接收”换“发送”成为可能。此解调算法能在发送端不使用其他功放线性化手段的情况下采用高阶QAM调制，提高功放的电源效率，保证通信速率的同时降低无线数据采集节点的体积、成本与功耗。

参考文献

　　[1] 丁娟，刘三阳，张平.基于能量优化的WSN数据收集和融合算法[J].电子技术应用，2013，39(5)：97-99.

　　[2] CHANG G K，LIU C，ZHANG L.Architecture and applica-tions of a versatile small-cell, multi-service cloud radio access network using radio-over-fiber technologies[C].ICC，：879-883.

　　[3] 曾德军，石栋元，李金政，等.基于双核NiosⅡ系统的数字预失真器设计[J].电子技术应用，2012，38(6)：10-12.

　　[4] GUERRERO N，CABALLERO A，AMAYA F，et al.Experimen-tal 2.5 Gbit/s QPSK WDM coherent phase modulated radio-over-fiber link with digital demodulation by a K-means algorithm[C].ECOC，Vienna，2009：1-2.

　　[5] GONZALEZ N，ZIBAR D，Yu Xianbin，et al.Optical phase-modulated radio-over-fiber links with K-means algorithmfor digital demodulation of 8PSK subcarrier multiplexed  signals[C].OFC，San Diego，2010：1-3.

　　[6] NAZEER K A A，KUMAR S D M，SEBASTIAN M P.En-hancing the K-means clustering algorithm by using a O(n logn) Heuristic method for finding better initial cen-troids[C].EAIT，2011：261-264.

　　[7] Feng Jinmei，Lu Zhimao，Yang Peng，et al.A K-means clustering algorithm based on the maximum triangle rule[C].ICMA，IEEE，2012：1456-1461.

　　[8] REDMOND S J，HENEGHAN C.A method for initialising the K-means clustering algorithm using kd-trees[J].PatternRecognition Letters，2007，28(8)：965-973.

　　[9] ZENG X B，HU Q M，HE J M，et al.High power RF amplifier′s new nonlinear models[C].APMC 2005.