文献标识码: A
文章编号: 0258-7998(2014)11-0105-04
0 引言
参数化功率谱模型估计方法中基于信号相关函数的自回归(AR)模型具有多种良好的性能,在理论研究和工程应用中最为广泛。研究表明,水声、无线通信等信号常伴有较强的非高斯脉冲噪声[1-4],?琢稳定分布能够描述此类脉冲噪声,在非高斯非线性的信号处理中应用广泛。针对该类噪声的特点,参考文献[1]提出了基于分数低阶矩(Fractional Lower Order Moment,FLOM)的共变谱,但是由于方法中待估信号仍需进行二阶矩计算,在![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028224341700005745583.jpg) 值接近1时性能下降明显。参考文献[2]给出了分数低阶协方差(Fractional Lower Order Covariance,FLOC)的方法,克服了谱估计方法的不足。参考文献[3]提出了分数低阶协方差系数,使AR模型系数的估计值收敛能力增强,提高了估计性能,但增加了预设分数低阶值的数量,应用中影响了
值接近1时性能下降明显。参考文献[2]给出了分数低阶协方差(Fractional Lower Order Covariance,FLOC)的方法,克服了谱估计方法的不足。参考文献[3]提出了分数低阶协方差系数,使AR模型系数的估计值收敛能力增强,提高了估计性能,但增加了预设分数低阶值的数量,应用中影响了![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028250002500002986610.jpg) 谱估计的精度,对频率分辨能力影响更大。
谱估计的精度,对频率分辨能力影响更大。
近年来,相关熵理论[5]的提出为非高斯非线性信号处理带来了新的思路,基于相关熵的信号处理方法在脉冲噪声条件下的应用越来越受到重视[4]。相关熵函数是一种新的表征信号局部相似程度的度量形式[6]。由于相关熵对非高斯非线性过程并不敏感,相关熵及由其演化的最大相关熵准则已广泛应用到多个方面[4-7]。本文将相关熵函数运用到AR模型参数估计中,建立了基于相关熵的AR模型参数估计方法,并通过AR模型参数得到![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028251413500001879511.jpg) 谱估计。本文方法无需预设分数低阶值,仿真显示在相同混合信噪比下能够在更大的脉冲特性范围内进行有效的
谱估计。本文方法无需预设分数低阶值,仿真显示在相同混合信噪比下能够在更大的脉冲特性范围内进行有效的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028250914300001404027.jpg) 谱估计。
谱估计。
1 ![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027640051300009374214.jpg) 稳定分布噪声及
稳定分布噪声及![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027641883200008870133.jpg) 谱
谱
1.1 ![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027640900500003434023.jpg) 稳定分布噪声
稳定分布噪声
?琢稳定分布是目前唯一符合广义中心极限定理的分布类型[1],通常由特征函数进行表征。如果随机变量?锥存在4个参数(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027642842200006061371.jpg) ,
,![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358027643730900002408327.jpg) ,?酌,a),其中0<
,?酌,a),其中0<![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027644669000004772442.jpg) ≤2,-1≤
≤2,-1≤![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358027645697800005753128.jpg) ≤1,a为实数,其特征函数:
≤1,a为实数,其特征函数:
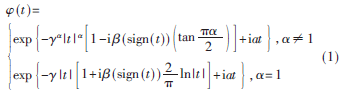
式中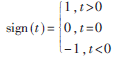 ,则称X服从?琢稳定分布,记为
,则称X服从?琢稳定分布,记为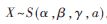 。
。
![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027652197700007733361.jpg) 称特征指数,表征分布的脉冲特性,值越小分布的拖尾越厚,反之拖尾变薄。称对称参数,确定分布的偏斜程度,
称特征指数,表征分布的脉冲特性,值越小分布的拖尾越厚,反之拖尾变薄。称对称参数,确定分布的偏斜程度, =0为对称分布,称为对称
=0为对称分布,称为对称![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027652881700001143814.jpg) 稳定(S)分布,-1≤<0为左偏斜分布,0<
稳定(S)分布,-1≤<0为左偏斜分布,0< ≤1为右偏斜分布。为分散系数,表征样本相对于均值的分散程度。a为位置参数,用于确定PDF的位置。
≤1为右偏斜分布。为分散系数,表征样本相对于均值的分散程度。a为位置参数,用于确定PDF的位置。
除这3种情况外,稳定分布的PDF没有封闭的表达式。
1.2 S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028228039800001537892.jpg) S分布下的模型
S分布下的模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028228925900008641511.jpg) 谱
谱
S?琢S分布具有很多优良的性质,应用广泛。随机过程X(n)的AR模型,可表示为[1]:
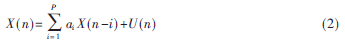
其中ai为AR模型参数,P为模型阶数,U(n)~S(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028099599800006520429.jpg) ,0,
,0,![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028100696500002574643.jpg) ,0)噪声,如果
,0)噪声,如果![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028229944000004823258.jpg) 满足1<
满足1<![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028230520800009873036.jpg) ≤2,则:
≤2,则:
E[X(n+l)|X(n)]=![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028231321000008672349.jpg) (l)X(n)(3)
(l)X(n)(3)
其中?姿(l)为X(n+l)与X(n)的共变系数。由式(2)和式(3)可以得到AR模型的广义Yule-Walker方程:
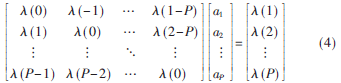
经过推导,S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028104496800009713535.jpg) S分布下的AR模型?琢谱表示为[1]:
S分布下的AR模型?琢谱表示为[1]:
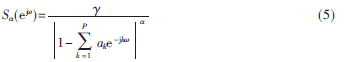
2 基于分数低阶统计量的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028232513400003059053.jpg) 谱估计
谱估计
2.1 基于FLOM的AR模型谱![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028107826900001635905.jpg) 估计
估计
基于FLOM的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028108929500001704211.jpg) 谱估计方法是通过随机过程的共变系数来计算AR模型参数的。X(n)和X(n+l)的共变系数为:
谱估计方法是通过随机过程的共变系数来计算AR模型参数的。X(n)和X(n+l)的共变系数为:
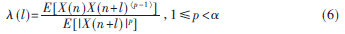
其中x〈p〉=sign(x)|x|p,p为分数低阶的阶数值。
对于有限的观测序列X(n),参考文献[1]给出了共变系数?姿(l)的估计值:
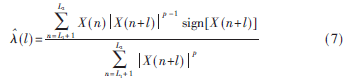
其中L1=max(0,-l),L2=min(N-l,N),l=-P:P(P为AR模型阶数),p为分数低阶的阶数值,N为观测序列数量。将式(7)代入式(4)可求得AR模型的参数估计值i(i=1,2,…,P)。将i代入式(5)可得不过,该方法不满足各态遍历定理,估计精度在较大脉冲条件下下降明显[3]。
2.2 基于FLOC的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028116032200004749847.jpg) 谱估计
谱估计
由于FLOM方法中共变系数![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028236605400001966171.jpg) (l)具有理论上的局限性,参考文献[2]提出了两个S
(l)具有理论上的局限性,参考文献[2]提出了两个S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028235439500009365847.jpg) S随机过程X1(n)与X2(n)之间的FLOC表达式:
S随机过程X1(n)与X2(n)之间的FLOC表达式:
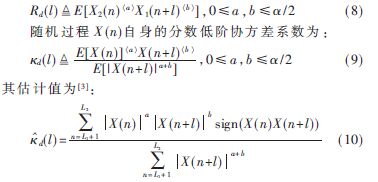
其中L1=max(0,-l),L2=min(N-l,N),l=-P:P,a和b为分数低阶的阶数值,N为样本数量。将式(10)的估计值代入式(4)进行求解,即可得到AR模型的参数 i(i=1,2,…,P)。将
i(i=1,2,…,P)。将 i代入式(5)得到AR模型的
i代入式(5)得到AR模型的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028126168400007164781.jpg) 谱估计该方法估计精度得到了很大提高,频率分辨能力也很强,但是其增加了分数低阶取值参数,需对a和b两个参数进行预先确定,给实际运用带来不便,且影响估计精度。
谱估计该方法估计精度得到了很大提高,频率分辨能力也很强,但是其增加了分数低阶取值参数,需对a和b两个参数进行预先确定,给实际运用带来不便,且影响估计精度。
3 基于相关熵的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028128034200003461172.jpg) 谱估计
谱估计
3.1 相关熵函数
Santamaria根据核空间向量的内积定义了一种广义的相关函数[6](Generalized Correlation Function,GCF),也称相关熵函数,具有与相关函数相似的性质。
若xt为一个随机过程,t∈T,则xt的相关熵函数为:

由式(13)可知,相关熵函数包含了随机变量(xt-xs)所有的偶数阶矩,能够更加准确地刻画信号特性,同时各偶阶矩都受到核尺寸的影响。在实际应用中,核尺寸值常用Silverman准则进行确定。高斯过程的Silverman准则[6]为:
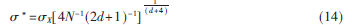
其中,确定的核尺寸值,X为随机变量样本的标准偏差,N为样本数,d为样本维数。
3.2 基于相关熵的AR模型参数估计
实际有限的信号样本条件下,离散时间严格平稳随机过程的相关熵函数可估计为[7]:
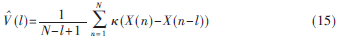
其中,N为样本个数,?资(·)为高斯核函数,l=-P:P(P为AR模型阶数)。同理,将所估计的相关熵函数值(l)代入式(4)得:
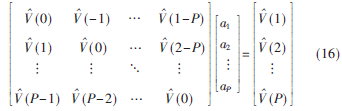
由于相关熵函数具有偶对称的性质,式(16)左边相关熵函数矩阵为P×P的正定Toeplitz矩阵[6],求解式(16)可以得到AR模型的参数i(i=1,2,…,P)。将i代入式(5)可得到AR模型的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028208856600005679219.jpg) 谱估。该方法不用预先设置分数低阶值,能够避免因设置的非最优性而对估计精度造成不良的影响。
谱估。该方法不用预先设置分数低阶值,能够避免因设置的非最优性而对估计精度造成不良的影响。
4 仿真实验与分析
4.1 混合信噪比
在![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028243211600006008906.jpg) 稳定分布噪声条件下,采用混合信噪比(MSNR)[2]来表示信号与噪声能量之比:
稳定分布噪声条件下,采用混合信噪比(MSNR)[2]来表示信号与噪声能量之比:
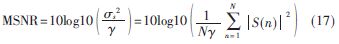
其中?酌为?琢稳定分布噪声的分散系数,N为信号样本数,S(n)为有用信号样本。
4.2 单正弦信号的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028212722100002120884.jpg) 谱估计性能
谱估计性能
设观测序列为X(n)=S(n)+U(n)=Acos(2?仔fn)+U(n),n=1,2,…,N。其中S(n)为信号序列,U(n)为噪声序列,A为信号幅度,f∈(0,0.5)为归一化频率,N为观测序列长度。
U(n)设为标准S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028217162000005368989.jpg) S分布,特征指数
S分布,特征指数![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028213396400009801325.jpg) =0.5,1.0,1.5,幅度A根据MSNR的取值相应设置,取MSNR=-3 dB,归一化频率f1=0.1,AR模型阶数P=30。FLOM方法中p=1,FLOC方法中a=0.1,b=
=0.5,1.0,1.5,幅度A根据MSNR的取值相应设置,取MSNR=-3 dB,归一化频率f1=0.1,AR模型阶数P=30。FLOM方法中p=1,FLOC方法中a=0.1,b=![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028215391300005932507.jpg) /2,而相关熵方法中并不需要提前设定这些参数。为消除信号随机影响,实验经过20次蒙特卡洛仿真后取均值。
/2,而相关熵方法中并不需要提前设定这些参数。为消除信号随机影响,实验经过20次蒙特卡洛仿真后取均值。
图1分别给出了FLOM、FLOC和相关熵3种方法的仿真结果。FLOM法在脉冲水平较低时(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028216452600006942911.jpg) =1.5)估计性能良好,能够准确估计出信号频率。FLOC方法在中等(
=1.5)估计性能良好,能够准确估计出信号频率。FLOC方法在中等(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028214126200003458183.jpg) =1.1)和较低(
=1.1)和较低(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028214755900008066630.jpg) =1.5)脉冲水平时估计效果均最为优异。本文方法由于对脉冲噪声不是十分敏感,不仅能够准确估计出有用信号频率,而且在各种脉冲特性水平情况下均非常稳定。随着脉冲特性逐渐提高,FLOM和FLOC法分别在?琢=1.1和?琢=0.5时相继失效。
=1.5)脉冲水平时估计效果均最为优异。本文方法由于对脉冲噪声不是十分敏感,不仅能够准确估计出有用信号频率,而且在各种脉冲特性水平情况下均非常稳定。随着脉冲特性逐渐提高,FLOM和FLOC法分别在?琢=1.1和?琢=0.5时相继失效。
4.3 双正弦信号![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028217754200004461044.jpg) 谱估计的频率分辨性能
谱估计的频率分辨性能
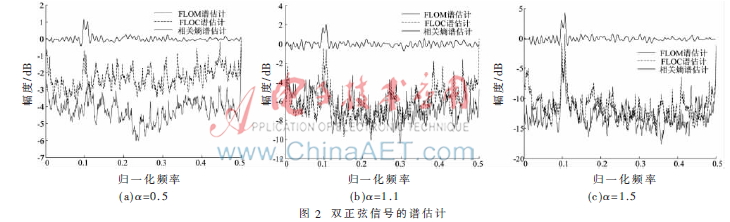
增加一个归一化频率为f2=0.11的同幅度信号,即S(n)=A(cos(2?仔f1 n+)+cos(2f2 n)),AR模型阶数P=100,MSNR、p、a和b设置同上节,实验方法不变。图2分别给出3种![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028219135200009498638.jpg) 谱估计方法对信号频率的分辨能力。
谱估计方法对信号频率的分辨能力。![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028221870000002613033.jpg) =1.5时,3种方法均能准确分辨0.01的频率差;
=1.5时,3种方法均能准确分辨0.01的频率差;![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028218650700003065430.jpg) =1.1时,FLOM方法失效,FLOC方法性能降低;脉冲特性水平提高到?琢=0.5时,这两种失效。本文提出方法在三种情况下均能分辨出相邻两个信号的频率,并且频谱也十分稳定。
=1.1时,FLOM方法失效,FLOC方法性能降低;脉冲特性水平提高到?琢=0.5时,这两种失效。本文提出方法在三种情况下均能分辨出相邻两个信号的频率,并且频谱也十分稳定。
5 结论
脉冲噪声存在于多种信号之中,常规AR谱估计方法性能下降明显。虽然分数低阶矩谱估计方法表现出了良好的性能,但需要提前设置分数低阶矩的阶值参数,具有一定的盲目性,影响了估计精度,其性能也随着噪声脉冲特性水平的提高逐渐下降。相关熵是表征信号间局部相似度的新度量形式,对信号的非高斯特性并不敏感。本文将相关熵函数引入脉冲环境下的AR模型参数估计中,仿真实验表明,新方法具有不必预设分数低阶参数、性能稳健的特点,与基于分数低阶统计量的?琢谱估计方法相比,在大脉冲条件下仍能保持良好估计效果。
参考文献
[1] MIN S,NIKIAS C L.Signal processing with fractional lowerorder moments: stable processes and their applications[J].
[2] XIN Y M,NIKIAS C L.Joint estimation of time delay andfrequency delay in impulsive noise using fractional lowerorder statistics[J].IEEE Transactions on Signal Processing,1996,44(11):1669-2687.
[3] 王首勇,朱晓波,李旭涛,等.基于分数低阶协方差的ARSαS模型α谱估计[J].电子学报,2007,35(9):1637-1641.
[4] 邱天爽,张金凤,宋爱民,等.脉冲噪声下基于广义类相关熵的DOA估计新方法[J].信号处理,2012,28(4):463-466.
[5] SANTAMARIA I,POKHAREL P P,PRINCIPE J C.Gener-alized correlation function:definition, properties,and appli-cation to blind equalization[J].IEEE Transactions on SignalProcessing,2006,54(6):2187-2197.
[6] LIU W F,POKHAREL P P,PRINCIPLE J C.Correntropy:a localized similarity measure[C].IJCNN′06.Vancouver,2006:4919-4924.
[7] 袁宵,唐涛,李禹,等.基于相关熵的MACH滤波器[J].国防科技大学学报,2012,34(6):153-157.

