文献标识码: A
文章编号: 0258-7998(2014)11-0113-03
0 引言
协作中继技术[1-2]能提高无线通信网络的覆盖范围和可靠性,克服多径无线多径衰落,受到学者的广泛关注。合理的功率分配能提高协作系统的资源利用率,提升系统的容量和性能[3-4]。近年来,仿生智能算法逐渐被用于解决最优化问题[5-8]。量子遗传算法继承了传统遗传算法的高效并行的优点,具有种群规模小、搜索能力强、收敛速度快且最优解稳定性高等特点,能有效解决多目标的资源最优化问题。在量子遗传算法的研究中,参考文献[6]研究了基于量子遗传算法的认知无线网络多目标函数优化问题;参考文献[7]研究了混沌理论,并对量子遗传算法进行了改进;参考文献[8]研究基于量子遗传算法的网络优化方法。目前,还没有相关文献将量子遗传算法应用到多中继系统的功率分配问题中。
本文考虑多中继协作系统,以最大化系统容量为目标,研究了基于量子遗传算法的多中继协作系统的功率分配方案。在该算法中,通过量子遗传算法得到渐进最优的功率分配方案,实现了传输比特差错率最小化。
1 系统模型
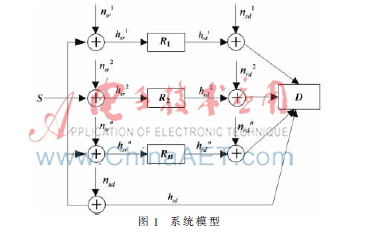
多中继无线协作系统如图1所示,系统由源节点S、目的节点D和n个潜在的中继节点Ri(i=1,2,…,n)组成,n、nsd为信道噪声;hsd为信道系数。采用半双工工作方式,整个传输过程采用TDMA传输方式,每次传输过程分为两个阶段。第一阶段:源节点分别向所有中继节点和目的节点发送信息;第二阶段,源节点沉默,中继节点将广播阶段接收到的信息放大转发给目的节点。
完整的一次传输过程需要n+1个时隙,由香农定理可知系统容量为:

其中,C为系统容量,r0为直传链路的瞬时信噪比,Es为源节点发送功率,|hsd|2为链路S-D的功率增益;信道噪声功率,rk为第k条中继链路的瞬时信噪比(k=1,2,…n),记为:

其中|h|2和为链路S-Rk、Rk-D的功率增益,Prk为第k个中继的发送功率,为对应链路的噪声功率。
功率分配优化模型记为:
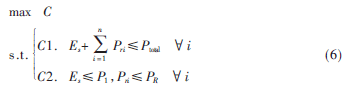
其中P1和PR分别为源节点和中继节点的最大传输功率,Ptotal为总功率。
2 基于量子遗传算法的功率分配
以比特差错率为准则,以最大信道容量为目标,利用量子遗传算法[9-10]迭代求出多中继系统的功率分配方案。
基于量子遗传算法的流程如下,流程图如图2所示。

(1)初始化种群;
(2)测量所有个体,可获取种群的一个状态;
(3)计算每个个体的适应度值,对最佳个体和其相应的适应度值予以保存;
每个个体的适应度定义如下:

(4)while(不能满足终止条件时)do
t=t+1;
测量种群中全部个
体获取个体状态;
对所有个体适应度
进行计算;
使用量子旋转门更
新个体;
保存最佳个体和其
相应的适应度值;
End
3 仿真结果与分析
本文在静态瑞利信道无线环境下对基于量子遗传算法的功率分配方案、基于遗传算法的功率分配方案和等功率分配方案进行了仿真,在仿真过程中,采用BPSK调制,最大选取了6个中继参与协作。对于量子遗传算法参数,设置种群大小为100,种群最大迭代次数为100,个体位串为20,交叉概率0.65,变异概率0.35。
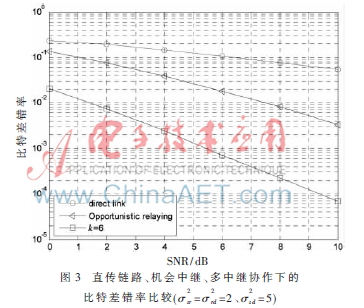
在基于量子遗传算法的功率分配方案中,本文对直传链路(direct link)、机会中继(Opportunistic relaying)及多中继(中继个数k=6)的比特差错率进行了比较,如图3所示。随着信噪比的增加,相对于直传链路,机会中继和多中继协作下能获得更小的比特差错性能。
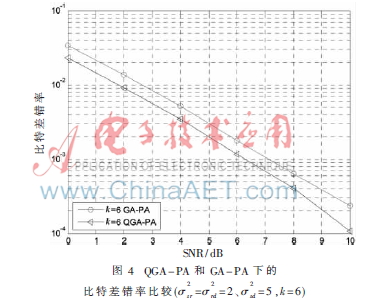
基于遗传算法与基于量子遗传算法的功率分配方案中,比特差错率比较如图4所示。基于量子遗传算法的功率分配(QGA-PA)策略能获得较小的比特差错率,优于基于遗传算法的功率分配(GA-PA)策略。
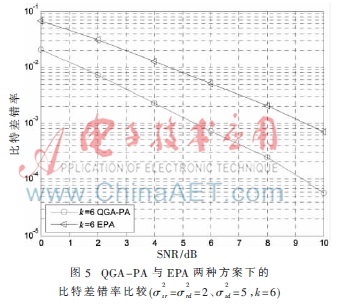
基于量子遗传算法的功率分配方案和等功率分配方法的比特差错率比较如图5所示。当信噪比变化时,从量子遗传算法与等功率分配方案的比特差错率比较,可以明显地看出,基于量子遗传算法的功率分配(QGA-PA)策略的比特差错率小于等功率分配(EPA)策略。

3种功率分配方案的比特差错率比较如图6所示,遗传算法功率分配策略的比特差错率小于等功率分配(EPA)策略;基于量子遗传算法的功率分配(QGA-PA)策略的比特差错率小于遗传算法功率分配(GA-PA)策略。与两种方案相比,基于量子遗传算法能获得更好的系统性能。
4 结论
本文研究了多中继协作系统的功率分配策略,将量子遗传算法应用到多中继协作通信系统的功率分配中,给出了功率分配算法步骤,提出了基于量子遗传算法的功率分配方案。该功率分配算法简单,只需给出优化目标函数,就能迭代求出接近最优的功率分配。在不同环境下,本文验证了基于量子遗传算法的功率分配方案比基于遗传算法的分配方案和等功率分配方案能获得更好的BER性能,为多中继资源分配提高了一种新的优化方法,有助于资源分配的应用。
参考文献
[1] KRISHNA R,CUMANAN K,Xiong Zhilan,et al.A novel cooperative relaying strategy for wireless networks with signal quantization[J].IEEE Transactions on Vehicular Technology,2010,59(1):485-489.
[2] LIU K.Temporal reuse in cooperative relay networks via destination feedback[J].IEEE Transactions on Vehicular Technology,2014(99):1-11.
[3] Jiang Fan,Wang Benchao.A cooperative bandwidth and power allocation strategy based on game theory in multi-relay networks[C].7th International Conference on WirelessCommunications,Networking and Mobile Computing (WiCOM),Wuhan,2011:1-5.
[4] BAIDAS M W,KUWAIT S,MACKENZIE A B.An auction mechanism for power allocation in multi-source multi-relaycooperative wireless networks[J].IEEE Transactions on Wireless Communications,2012,11(9):3250-3260.
[5] 张利强,全厚德,崔佩璋.基于改进粒子群算法的宽带测向阵列结构优化[J].电子技术应用,2013,39(3):108-111.
[6] Wang Huan,Guo Lili.Multi-objective optimization of cognitiveradio in Clonal selection quantum genetic algorithm[C].International Conference on Measuring Technology and Mechatronics Automation(ICMTMA),Changsha City,2010:740-743.
[7] Teng Hao,Zhao Baohua,Yang Bingru.An improved mutativescale chaos optimization quantum genetic algorithm[C].International Conference on Natural Computation ICNC′08.Fourth,Jinan,2008:301-305.
[8] Fan Xin,Li Wei,Chen Zhihuan,et al.Network optimizationmethod based on improved quantum genetic algorithm[C].International Symposium on Information Science and Engineering(ISISE),Shanghai,2012:422-425.
[9] 赵知劲,彭振,郑仕链,等.基于量子遗传算法的认知无线电频谱分配[J].物理学报,2009,58(2):1358-1363.
[10] 杨俊安,庄镇泉,史亮.多宇宙并行量子遗传算法[J].电子学报,2004,32(6):923-928.

