0 引言

　　卫星通信在传播过程中由于其信号的广播性容易遭到第三方接收机的窃听，因此卫星通信的安全传输问题一直是人们关注的焦点[1-2]。现有的卫星网络的信息安全主要通过上层安全协议来实现，如验证、鉴权和记账（AAA）协议，IP安全（IPSEC）协议[1]等。但是随着计算机运算能力的飞速发展，基于计算量的传统加密机制受到了严峻的挑战。

　　近年来，物理层安全技术受到了广泛关注，尤其是利用多天线系统的信道差异性、互易性等特性和波束成形、天线选择和干扰辅助等策略来增强网络的安全性取得了显著的进展[3-4]，可在满足一定的功率、带宽和复杂度的条件下显著提高系统的安全性。然而，国内外针对多波束卫星网络中的物理层安全技术的研究和应用才刚刚起步。

　　本文将物理层安全技术应用到多波束卫星通信系统下行传输中。首先，建立多波束卫星物理层安全通信系统模型。随后，以最大保密和速率作为该系统的保密性能评价指标，介绍并仿真了迫零（Zero-Forcing，ZF）和增强信漏噪比（Enhanced Signal-to-Leakage-and-Noise Ratio，E-SLNR）两种波束成形算法。仿真结果表明，E-SLNR波束成形算法不仅不受限于天线数目，而且获得了更好的安全性能。

1 系统模型

　　本文考虑多波束卫星通信系统中的下行链路，其中卫星工作在Ka波段。如图1所示，假设多波束卫星通信系统通过对M个天线元进行处理（例如波束成形），形成K个波束（K≤M），假设有K个用户处于这K个波束的共同覆盖范围内，故这K个波束能够在相同频段内为K个用户提供服务。在K个波束的共同覆盖范围内出现一个被动窃听者，用e表示，它将窃听多波束卫星发送的信息[2-3]。

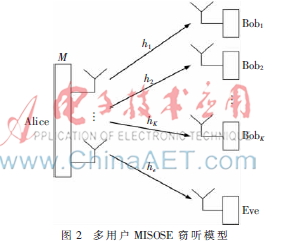
　　假设所有用户和窃听者都是单天线接收者，多波束卫星网络物理层安全模型可建模成如图2所示的多用户MISOSE（Multiple-input Single-output Single-antenna Eavesdropper）窃听模型，即在存在单个被动窃听用户Eve的情况下，拥有M个天线元的Alice与K个单天线合法用户Bobs进行安全通信。

　　假设sk为多波束卫星发送给第k个用户的保密信号，并且该信号功率归一化为1，即E{|sk|2}=1。定义Pk为第k个波束分配的功率，因此P=[P1，P2，…，PK]T是所有波束的功率分配矢量。所有信号通过波束成形权值矢量wk∈CM调制到天线阵上。这里，波束成形矩阵W定义为W=[w1，w2，…，wK]∈CM×K。不失一般性，假设||wk||=1。从而，每一个波束的发送功率为Pk·E|sk|2=Pk。

　　如图3所示，第k个用户和窃听者Eve接收到的信号分别表示为：

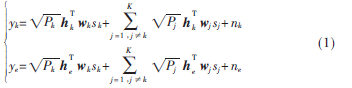
　　其中hk∈CM，he∈CM分别表示多波束卫星到第k个用户之间的合法信道向量和多波束卫星到窃听者Eve之间的窃听信道向量。标量nk和ne分别表示第k个用户和Eve端的零均值复高斯噪声，方差分别为。

　　根据式（1），第k个用户和窃听者对第k个数据流的信干噪比（Signal-to-Interference-Plus-Noise Ratio，SINR）分别表示为：

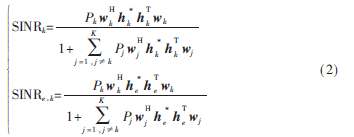
2 最大化保密和速率的波束成形算法

　　为了评价物理层安全通信系统的安全性能，不同的安全需求和应用环境下需要采用不同的评价指标。当发送端已知合法接收端和窃听者的信道信息时，一般采用保密容量（Secrecy Capacity）作为安全评价指标。而当系统中存在多个用户时，由于需要考虑多个用户的保密容量，计算其保密容量域是一项很困难的工作，此时可采用最大保密和速率来衡量整个系统的安全性。

　　本文在卫星发送总功率约束下，通过设计波束成形矢量wk和功率分配Pk，最大化系统的保密和速率，相应优化问题可以表示为[5]：

　　下面介绍迫零（ZF）和增强信漏噪比（E-SLNR）两种波束成形算法。其中，迫零算法要求卫星发送天线数目不小于用户和窃听者Eve天线数目之和，故本文假设M≥K+1。

　　2.1 迫零波束成形算法

　　ZF波束成形算法的基本思想是使得合法用户间干扰和窃听者的信号泄漏均为零。通过ZF波束成形选择的发送信号波束成形权值使得同信道干扰被抵消掉，也就是对于第k个数据流，当j≠k时，hwj=0。同时将窃听者泄漏完全置零，即对于第k个数据流。

　　因此，通过ZF波束成形算法设计的发送波束成形矩阵W=[w1，w2，…，wK]使得第k个用户和窃听者的SINR分别为：

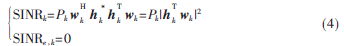
　　此时，最大化保密和速率问题转化为：

　　将最大化问题（6）的求解分为两步完成。首先，固定功率分配Pk，求解最佳波束成形矢量wk，即求解下面的最大化问题：

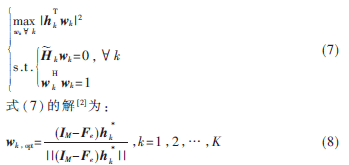
　　其中IM表示M阶单位矩阵，k的伪逆。

　　求解出最佳波束成形矢量wk，opt后，第二步则是求解最佳功率分配Pk，令rk=|hwk，opt|2，即求解下面的最大化问题：

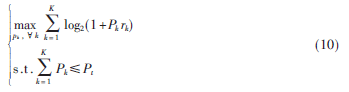
　　上述问题可以通过标准注水算法求解，

　　2.2 增强信漏噪比波束成形算法

　　Sadek等人在参考文献[6]中首次提出了信号泄漏的思想。对于某个接收用户而言，其他剩余用户对该用户造成的干扰称之为用户间干扰（Inter-User Interference，IUI），与之相反，信号泄漏指的是该用户对其他剩余用户造成的干扰。在物理层安全中，也正是合法接收端将信号功率泄漏到窃听者导致了保密信息的泄漏。

　　E-SLNR波束成形算法的基本思想是基于SLNR准则[7]，将合法用户间的信号泄漏和窃听者的信号泄漏统一进行波束成形矩阵设计。定义E-SLNR为合法用户接收信号功率与泄漏到其他合法用户及窃听用户的信号功率加噪声之比。即：

　　从式（15）可以发现，wk与分配给每个合法用户的功率Pk密切相关，因此，wk与Pk的联合优化问题是一个NP hard 问题，虽然可以通过交替迭代优化算法求得次优解，但是由于SINRk和SINRe，k存在信号交叉，wk与Pk联合优化问题的求解更加困难。故本文只考虑等功率分配（Equal Power Allocation，EPA）情况下的E-SLNR问题的求解，即：

3 仿真结果与分析

　　本节通过MATLAB仿真Ka波段多波束卫星物理层安全通信下所提出的ZF和E-SLNR波束成形算法的安全性能。由于ZF波束成形算法要求M≥K+1，在仿真中，均假设M=K+1。

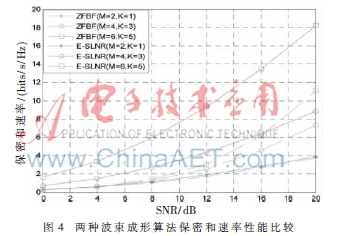
　　图4比较了不同发送天线元数目M、用户数目K情况下的ZF和E-SLNR波束成形算法的保密和速率性能。从图中可见，E-SLNR算法性能明显优于ZF算法的性能。这是因为E-SLNR算法不用限制要求窃听者的信号泄漏或用户间干扰为零，而是统一考虑两种泄漏，因此，即使不进行功率分配的优化配置也能获得较好的安全性能。而ZF算法要求用户间干扰和窃听者的信号泄漏均为零，虽然降低了计算复杂度，但是损失了一定的安全性能。

　　图5仿真了两种波束成形算法的保密和速率与用户数目K的关系。从图中可见，随着合法用户数目K的增加，两种波束成形算法的安全性能均随之增加，但ZF算法的安全性能变化平缓，在高用户数目K下将趋近于一个常数。这是因为ZF算法要求用户间的干扰为零，故随着用户数目K的增大，需要损失更多的安全性能来满足这一要求。

4 结论

　　本文将物理层安全技术应用到多波束卫星通信系统下行传输中，建立了多波束卫星物理层安全通信系统模型。针对多波束卫星通信系统物理层安全模型中保密容量难以计算和波束间干扰导致信号交叉的问题，以最大化保密和速率作为该系统的安全性能评价指标，仿真并比较了ZF和E-SLNR两种波束成形算法的性能。仿真结果表明，E-SLNR算法不仅不受限于天线数目，且其安全性能明显优于ZF算法的性能。

　　参考文献

　　[1] LIANG L，IYENGAR S，CRUICKSHANK C，et al.Security for flute over satellite networks[C].In Proc.of Inter.Con-ference Communication Mobile Computing，2009：485-491.

　　[2] LEI J，HAN Z，VZQUEZ-CASTRO M ，et al.Secure satellite communication systems design with individual secrecy rate constraints[J].IEEE Transactions on Informa-tion Forensics and Security，2011，6(3).

　　[3] OGGIER F，HASSIBI B.The secrecy capacity of the MIMOwiretap channel[J].IEEE Trans.Inf.Theory，2011，57(8)：4961-4972.

　　[4] PEI M Y，WEI J，WONG K，et al.Masked beamforming forMIMO wiretap channels with imperfect CSI[J].IEEE Trans.on Wireless Communications，2012，11(2).

　　[5] CHRISTENSEN S，AGARWAL R，CARVALHO E，et al.Weighted sum-rate maximization using weighted MMSE for MIMO-BC beamforming design[J].IEEE Trans.on Wireless Communications，2008，7(12)：4792-4799.

　　[6] SADEK M，TARIGHAT A，SAYED A H.A leakage-based precoding scheme for downlink multi-user MIMO channels[J].IEEE Trans.on Wireless Communications，2007，6(5)：1711-1721.

　　[7] WANG K，WANG X，ZHANG X.SLNR-based transmit beamforming for MIMO wiretap channel[J].Wireless Personal Communications，2013，71(1)：109-121.