0 引言

    在大规模集成电路发展的今天，随着高精度、便携式电子器件的进一步发展，传统的信号处理技术已经逐步被大规模的并行处理技术所取代。剩余数系统以其特有的进位自由和并行运算特性，近年来已经成为高速、大规模数字信号处理的最好选择。

    剩余数系统应用的意义已经被证明，尤其对于处理密集型加法、减法以及乘法等占有绝对的优势。然而，其他的运算例如除法、奇偶检测、比例变化、大小比较和符号检测等运算由于其运算的复杂性，在剩余数系统就失去了并行性的优势，这些运算有时不得不将余数转换成二进制数后再做运算，所以会浪费大量的电路面积和延迟。为了提高此类运算电路的性能，近年来许多研究人员开始对此领域进行研究,但是大部分研究针对比较常用的3模集合{2ⁿ，2ⁿ+1，2ⁿ-1}^[1-4]。

    比例变化是余数系统研究最重要问题之一，比例变化尤其在防止溢出和内部乘积处理方面具有举足轻重的作用。和反向转换一样，比例缩放在剩余数系统实现也涉及到大的延迟和较高的硬件复杂度，涉及在每一个剩余数计算阶段。本文针对4模集合{2ⁿ，2²ⁿ+1，2ⁿ+1，2ⁿ-1}，在分析反向转换和比例缩放算法的基础上，提出了一个新的基于2ⁿ的比例缩放算法，并基于加法器实现其VLSI结构。

1 算法描述

    基于剩余数系统模集合{m₁，m₂，…，m_n}的整数X，通过一个比例因子k做比例变化，设Y为比例变化的结果，则：

    对于模集合针对4模集合{m₁，m₂，m₃，m₄}其对应于{2ⁿ，2²ⁿ+1，2ⁿ+1，2ⁿ-1}，根据式(3)：

2 电路实现

2.1 y₁的硬件实现

    定理2：若0≤v≤2ⁿ-2，则v2ⁱ模2ⁿ-1的结果相当于将n位宽二进制数v，即v_n-1v_n-2…v₀循环左移i位^[5]。

    定理3：若0≤v≤2ⁿ-2，则(-v)2ⁱ模2ⁿ-1的结果相当于将v乘以2ⁱ模2ⁿ-1的结果按位取反^[5]。

    由前面的分析可知，对于模通道2²ⁿ进行2ⁿ比例变化结果y₁，直接取Y的低n位即可实现。应用定理1和2，通过进一步合并化简，Y最终转换为5个4n位操作数相加的形式，即：

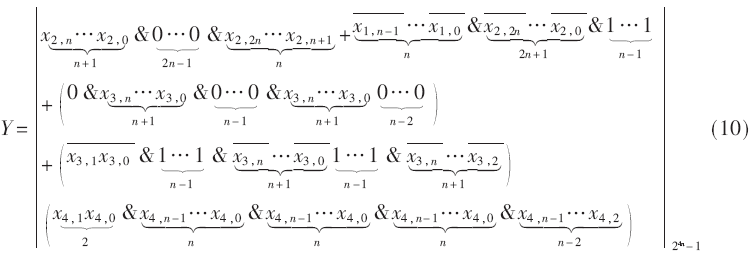
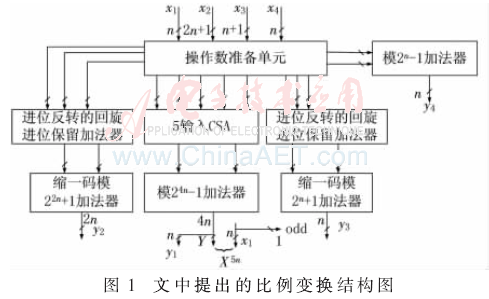
    通过3级进位保留加法器（CSA），最终形成两个4n位宽的S、C，S和C通过模2⁴ⁿ-1加法器得到4n位模加法器的结果Y，如图1所示。

2.2 y₂的硬件实现

    操作数在进入缩一码模2²ⁿ+1加法器之前必须分别减1，而缩一码模2²ⁿ+1加法器在输出以后必须加1才能得到真正的结果。两者合并，只要将进位加法器的输出减1即可。同时，根据定理4，进位保留加法器的最高有效位的进位输出将被直接取反加到下一级进位保留加法器的最低有效位的同时，需要加上一个补偿常数因子2ⁿ。联合前面缩一码模2²ⁿ+1加法器的校正因子-1，总的校正项C_j为：

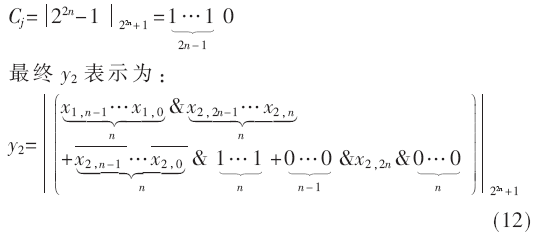
    直接将上面的三项输入法进位反转的回转进位保留加法器，得到进位2n位C和2n位和位S，将C和S直接输入到缩一码模2ⁿ+1加法器，该缩一码模2n+1加法器的输出即为实际的比例变换结果。

2.3 y₃的硬件实现

    y₃的实现和y₂相似，同样通过进位保留加法器树和一个缩一码模2²ⁿ+1加法器实现。通过化简式(7)：

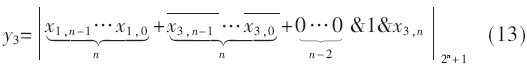
    设校正项为C_j，同理，总的校正因子C_j为：

2.4 y₄的硬件实现

    对于模通道m₄=2ⁿ-1进行2ⁿ比例变化结果y₄，根据式(8)，应用定理2，进一步表示为：

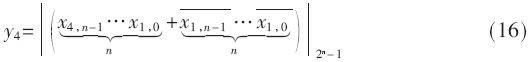
    该模通道比例变化y₄的实现只需要将上面的两个n位操作数直接通过一个0唯一表示的模2ⁿ-1加法器，即可实现。

    整个基于4模集合{2ⁿ，2²ⁿ+1，2ⁿ+1，2ⁿ-1}的反向转换以及比例转化的硬件结构图如图1所示。

3 性能评估和比较

    为了进行定性评估，本文与同样对4模集合2n比例变换文献[4]的理论模型进行对比。采用文献[4]提出的门单位计算方法，用近似门单位模型方法计算其硬件以及信号处理延时，即2输入异或门（XOR）或者同或门（XNOR）的面积和延迟按照2个单位计算，一个全加器（FA）等同于7个单位的面积和4个单位的延迟，非门（NOT）的面积和延迟都以0计算，其他基本的二输入逻辑门面积和延迟按照1个单元计算。为了更加公平的对比，本研究和文献[4]所有的模2ⁿ-1加法器均采用目前最优化的0唯一表示的并行前缀模2ⁿ-1加法器^[6]，缩一码模2ⁿ+1加法器采用文献[7]提出的模加法器模型。提出的新的比例变换模型各个通道面积理论数据如表1所示，和其他模集合比例转换器面积和延时对比如表2所示。从中可以看出，本文所提出的4比例变换器模型，在动态范围大的情况下，在硬件复杂度方面占有绝对的优势。

4 结论

    余数系统的比例变换是避免在剩余数系统的中间运算过程中发生溢出错误的主要方法。基于此，针对4模集合{2ⁿ，2²ⁿ+1，2ⁿ+1，2ⁿ-1}，在分析反向转换和比例缩放算法的基础上，提出了一个新的反向转换和基于2n的比例缩放算法，并基于加法器实现其VLSI结构，使该模集合能够得到更加广泛的应用。理论分析结果表明，在具有相同模通道数的同类比例变换器中，本研究的算法更加优化，硬件性能表现更加优异。

参考文献

[1] ANTONIO G，ANTONIO L.A look-up scheme for scaling in the RNS[J].IEEE Transactions on Computers，1999，48(7)：748-751.

[2] TAY T，CHANG C H，LOW J.Efficient VLSI implementation of 2n scaling of signed integer in RNS{2ⁿ-1，2ⁿ，2ⁿ+1，}[J].IEEE Transactions on Very Large Scale Integration(VLSI) Systems，2013，21(10)：1936-1940.

[3] YE Y，MA S，HU J.An efficient 2n RNS scaler for moduliset{2ⁿ-1，2ⁿ，2ⁿ+1，}[C].IEEE Symp.Inf.Sci.Eng.(ISISE)，Shanghai，China，2008.12：511-515.

[4] SOUSA L.2n RNS Scalers for Extended 4-Moduli Sets[J].IEEE Transactions on Computers，2015，62(12)：1-14.

[5] CAO B，CHANG C H，SRIKANTHAN T.A residue-to-binary converter for a new five-moduli set[J].IEEE Transactions on Circuits and Systems-I，2007，54（5）：1041-1049.

[6] PATEL R A，BENAISSA M，BOUSSAKTA S.Fast parallelprefix architectures for modulo 2n-1 Addition with a single representation of zero[J].IEEE Transactions on Computers，2007，56(11)：1484-1492.

[7] VERGOS H，EFSTATHIOU C，NIKOLOS D.Diminished-one modulo 2n+1 adder design[J].IEEE Transactions on Computers，2002，51(12)：1389-1399.

[8] Wang Yuke.Residue-to-binary converters based on new Chinese remainder theorems[J].IEEE Transactions.on Circuits and Systems-II，2000，47（3）：197-205.