0 引言

　　锂离子电池广泛应用于国防军事领域，涵盖了陆、海、空、天等诸多兵种，攸关信息产业和新能源产业的发展，更成为现代和未来军事装备不可缺少的重要能源。然而在其应用领域中仍有许多亟待破解的难题，电池健康状态（State of Health，SOH）预测[1]就是一个在研究电池使用过程中急需解决的重要问题。

　　健康状态是指电池从寿命开始到寿命结束期间所处的状态，它通常以百分比的形式表示，健康状态也可以被理解为电池经过长期使用后所处的退化程度。健康状态预测是指根据检测得到的电池电压、电流、内阻、温度等参数，通过一定的算法预测判断电池所处的健康状态以及可能出现的故障现象[1]。通过健康状态预测，可以使得在电池永久损坏前有足够的时间来采取适当的措施以预防事故的发生。

　　1999年Jaworski就提出用统计参数模型来预测无故障工作时间[2]。Blanke等建立了一种基于阻抗谱的电动/混合动力汽车车载电池容量预测模型[3]。Bhangu等将扩展卡尔曼滤波算法应用于电动车电池的SOH实时预测[4]。Kozlowski提出融合诸如自回归滑动平均数和神经网络等数据驱动算法来进行预测和诊断[5]。但当实际工作环境和负载条件与理想数据集不同时通过评估SOH来精确预测电池健康状态仍然面临技术难题[6]。为此，本文基于锂离子电池集总参数模型，提出一种可以融合电池测量数据的状态估计与预测算法，来实现其健康状态的精确预测。

1 基于模型的锂离子电池健康状态预测流程

　　电池健康状态的预测可以采用数据驱动、算法模型及两者综合的方式实现，此外也可采用电化学模型来描述电池内部动态过程[6]。基于阻容网络电路仿真实现的动态模型，适用于铅酸和镍氢电池，对锂离子电池而言还需要考虑非线性平衡电势、放电比率、温度、热效应和瞬态功率响应等因素的影响[7]，为此需要测量与电解液比重成函数关系的电压。

　　基于模型的预测使得产品在使用过程中能够提早预防，避免事故发生，在汽车、航空和国防工业中已经出现大量的基于模型预测的应用。因为系统模型在早期设计阶段已经被仿真，系统的可靠性和鲁棒性将获得最大幅度的提升。这些进展加速了基于模型的系统诊断和预测的一体化，由此产生了一种基于状态的维护策略，并且提升了系统的可靠性。如果有一个准确的系统仿真模型，诊断和预测就可以与系统设计同时综合起来。

　　一个系统导向的预测方法需要满足下列情况[8]：故障检测和基于检测的方法能随着系统元件退化而进行预测，能够减小任务危险程度和提升决策支持。这种预测不仅能解决个别元件的状况问题，还能处理这些状况对任务准备和采取恰当手段的影响。

　　基于模型的预测是假设一个准确的数学模型是存在的，其方法是使用残差作为特征，残差是一个实际的系统传感器测量数据和数学模型输入之间的一致性检查的结果。前提是存在故障的情况下残差很大，在正常的干扰、噪音和仿真误差的情况下残差又很小。统计技术用于定义阈值，以检测存在故障。基于模型的预测过程如图1所示[8]。

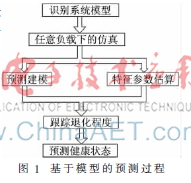
2 锂离子电池集总参数模型

　　锂离子电池由一对浸在电解液中的电极组成，化学驱动力来源于两个电极之间的化学势能差。例如在室温20 ℃，1个大气压条件下测得理论开路电压为E0，然而在实际使用过程中实际电压与E0之间有一个电压降，这个电压降主要是由电阻压降、活性极化、浓差极化三个方面引起的[6]。

　　完全表达内部电化学反应的锂离子电池模型很难求解计算而且缺少工程实用性。为此，可用近似的集总参数来表达锂离子电池内部不同因素引起的电压降，得到如图2所示的模型[6]。图中RE表示引起电阻压降的电解液电阻效应，电荷转移电阻RCT和并联的界面电容CDL表示活性极化，RW表示浓差极化。

　　应用集总参数模型在频域中通过电化学阻抗谱测量方法能做出奈奎斯特图，并由此更好地理解电池内部的降解过程，但需要特殊的测试设备并且满足最优测试条件。应用集总参数模型在时域中能得到电池放电曲线，因此可用来对电池健康状态进行评估和预测。表征电池健康状态的两个重要参数是电池的放电终止(End-of-Discharge，EOD)时间和寿命终止(End-of-Life，EOL)点。在此，选择放电终止时间作为预测参数。

3 基于粒子滤波算法的锂离子电池健康状态预测

　　3.1 锂离子电池健康状态表征参量

　　放电终止用放电循环中与电荷损耗成函数关系的阻抗参数来表示。随着电池的放电运行，内部电化学反应和电流流通将使得电池温度明显上升[9]，引起电解液离子的活性增加，导致Warburg阻抗RW下降。RW下降一段时间后自放电率将增加，这又会导致产生电解液阻抗RE。而且由于温度的升高，电池内的反应物消耗速度将加快，特别是在放电循环的末期尤为明显，这又会引起电荷转移电阻RCT的增加，并导致电池电压的突然下降，使电池失去工作能力，如图3所示。因此EOD可以用如下公式进行计算[6]：

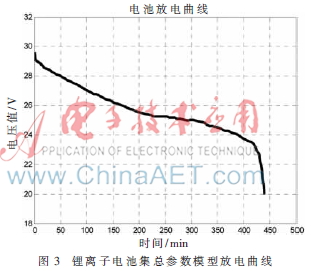
　　其中，Einit是放电循环的初始电压降，是由测试数据估计出经验系数。图3所示为锂离子电池集总参数模型放电曲线，  能很好地反应出电池电压随时间变化的关系，根据它可以预测出电池的放电终止时间。

　　3.2 基于粒子滤波算法的锂离子电池健康状态预测

　　公式化模型能用来描述锂离子电池健康状态，但有一系列未知参数需要识别，即使从测量数据能得到这些参数也不能直接应用，因为不同电池、同一电池的不同充电循环测得数据都可能不一样，而且给定循环参数值可能是非稳定的[10]。对于电池健康状态的预测，必须找到一种能容纳非高斯噪声的非准确、非线性、非稳态模型，粒子滤波提供了一种较为理想的解决方案[2]。

　　3.2.1 粒子滤波算法

　　粒子滤波（Particle Filter，PF）是指通过寻找一组在状态空间传播的随机样本对概率密度函数（Probability Density Function，PDF）进行近似，以样本均值代替迭代运算，从而获得状态最小方差分布的过程[11]。当样本数量N→∝时可以逼近任何形式的概率密度分布。与传统蒙特卡洛方法比较起来，序列重要性采样使得PF降低了精确预测近似分布所需的样本数[12]，具有快速性和高的计算效率。

　　PF方法的基本原理是以一系列点来近似条件状态概率分布p(zk/xk)，这些点被称之为粒子（来自未知空间的样本），包含了代表离散概率事件的权重因子[11]。

　　式（6）给出一个描述时间系统的演进非线性过程模型，式（7）是一系列可用的测量数据z1:k=(z1，…，zk)和状态PDF的初始估计p(x0)。估计过程包括两个主要步骤：预测和滤波。

　　预测过程用式（8）描述：

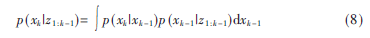
　　滤波环节用现态的观测值zk和先验状态PDF来生成后验状态PDF：

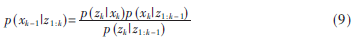
　　其中p(zk|z1:k-1)是规范化因子，与状态xk独立。后验概率密度p(xk|z1:k)无法用解析法求解，这可用如式（11）所示的一系列样本和第i次采样相对应的规范化重要性权重因子来近似。

　　其中，重要性函数q(xk|x0:k-1，z1:k)是p(xk|xk-1)的近似估计。

　　3.2.2 EOD预测

　　基于粒子滤波算法的EOD预测状态转移方程为：

　　其中，i为时间索引项，fs为采样频率，E为在i时刻测得的电压，wi和vi是相互独立的高斯噪声项。

4 实验及结果分析

　　实验选择天津力神电池股份有限公司生产的TBP0306型卫星地面接收站锂离子蓄电池组，额定容量9 Ah，标称电压25.2 V。

　　选定锂离子电池组放电循环中的电压变化为研究对象，利用式（12）、（13）作为状态转移方程，式（14）作为测量模型，粒子滤波算法估计的电压平均值和实际输出电压曲线如图4所示。

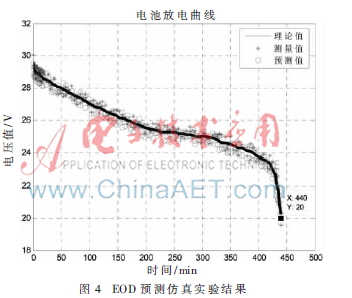
　　图中曲线“－”表示运用方程（1）计算出的理论放电电压值；点集“※”表示用测量模型(式14)仿真得到的测量电压值；点集“○”为用粒子滤波算法预测的电压值。预测过程仿真实验中选用与实际环境条件下得到的测量数据近似粒子，粒子数为300，放电曲线计算过程中考虑了高斯噪声项。通过仿真曲线可以看出，该锂离子电池组的放电终止时间为440分钟，即电池组在正常工作条件下可以工作440分左右。经过多次实验后，对比仿真实验结果，仿真曲线的一致性较高，残差在5%之内。

　　从仿真结果可以看出，粒子滤波算法能对锂离子电池组的放电终止时间给出正确的预测，进而可以预测电池组的健康状态。

5 结论

　　本文介绍了一种基于模型的系统预测过程，其能预测多种操作模式下的系统剩余寿命。通过对锂离子电池集总参数模型的分析，提出了利用粒子滤波来预测锂离子电池的健康状态参数。选择放电终止时间作为预测参数，利用粒子滤波算法对锂离子电池在放电循环中的电压平均值进行估算并与实际输出电压曲线进行比较。数据比较表明，粒子滤波算法能对锂离子电池健康状态给出正确的预测。

参考文献

　　[1] 陈召洪.“锂想国”探秘：新能源汽车带来的春之律动[R].万联证券新能源研究小组动力锂电池深度研究报告.2010，09.

　　[2] SAHA B，GOEBEL K，CHRISTOPHERSEN J.Comparison ofprognostic algorithms for estimating remaining useful life of

　　batteries[J].Transactions of the Institute of Measurement and

　　Control，2009，31(3-4)：293-308.

　　[3] BLANKE H，BOHLEN O，BULLER S，et al.Impedance on lead-acidbatteries for state-of-charge，state-of-healthand cranking capability prognosis in elec-tricand hybrid electric vehicles[J].Journal of Power Sources，2005，144(2)：418-25.

　　[4] BHANGU B S，BENTLEY P，STONE D A，et al.Nonlinear observersfor predicting state-of-charge and state-of-health of lead-acid batteries for hybridelectricvehicles [J].IEEE Transactions onVehicular Technology，2005，54(3)：783-94.

　　[5] KOZLOWSKI J D.Electrochemical cellprognostics using fusiontechniques[C].Aerospace Conference 2003，IEEE Proceedings，2003，7：3257-3270.

　　[6] DALAL M，MA J，HE D.Lithium-ion battery life prognostichealth management system using particle filtering framework[J].Proceedings of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2011，225(1)：81-90.

　　[7] GAO L，LIU S，DOUGAL R A.Dynamic lithium-ion batterymodel forsystem simulation[J].IEEE Transactions on Com-ponents and Packaging Technologies，2002，25(3)：495-505.

　　[8] Luo Jianhui，NAMBURU M，PATTIPATI K，et al.Model-based Prognostic Techniques[C].AUTOTESTCON 2003：330-340.

　　[9] SAHA B，GOEBEL K.Modeling Li-ion battery capacity depletion in a particle filtering framework[C].Annual Conference of the Prognostics and Health Management Society，San Diego，California，2009.

　　[10] 高安同，张金，陈荣刚，等.锂离子电池荷电状态估算及剩余寿命预测研究探讨[J].电源技术，2014，38(6)：1066-1068.

　　[11] 胡士强，敬忠良.粒子滤波算法综述[J].控制与决策，2005(04)：262-264.

　　[12] DOUCET D，FREITAS N D，GORDON N.Sequential  Monte Carlo methods in practice[M].Information Science and Statistics，Springer，2001.