摘  要： 对ISOMap、LDA、LLE、PCA这4种典型降维算法的主要思想和算法步骤进行了详细分析，并将它们用于有监督分类。从实验结果分析得到结论，其可为有监督分类提供有益的借鉴。

关键词： 维数约简；监督分类；样本外点问题

0 引言

　　随着信息技术和空间技术的快速发展，人类每天都可以获得海量的数据，很多数据往往都是高维的，例如生物基因序列分析、高光谱遥感图像处理等领域所要处理的数据。而高维数据难以被人理解、表示和处理[1]，降维是解决问题的一个可行途径。近年来，降维已经成为信息处理领域的一个研究热点。

　　在高维数据降维方面，目前使用的降维方法可分两大类：线性降维和非线性降维。比较有代表性的线性降维方法有：投影寻踪（Projection Pursuit，PP）[2]、主成分分析（Principal Component Analysis，PCA）[3]、多维尺度变化（MultiDimensional Scaling，MDS）[4]、独立成分分析（Independent Component Analysis，ICA）[5]、线性判别分析（Linear Discriminant Analysis，LDA）[6]、边际Fisher分析（Marginal Fisher Analysis，MFA）[7]、无监督判别映射（Unsupervised Discriminant Projection，UDP）[8]等。常见的非线性降维方法包括：局部线性嵌入（Locally linear Embedding，LLE）[9]、等距映射（Isometric Mapping，ISOMap）[10]、黎曼流形学习（Riemannian Manifold Learning，RML）[11]、多流形（Multiple Manifolds，MM）[12]、层次流形学习（Hierarchical Manifold Learning，HML）[13]等。

1 典型线性降维算法

　　1.1 LDA

　　LDA的基本思想是利用样本的类别标签信息，通过对样本集（X1，X2，…，Xk，…，XN）的总类内散布矩阵和总类间散布矩阵这两个带有类标签信息的统计量计算广义特征值，得到相应的映射矩阵，最后通过映射矩阵将样本从高维空间映射到低维空间。LDA算法的核心是广义特征值分解。不妨用N表示训练样本总数，num为类别总数，第k类样本的样本总数为Nk，Xk表示第k类训练样本特征向量的均值，X表示所有训练样本特征向量的均值，X（k）j表示第k类中的第j个样本，LDA的计算步骤如下[6]：

　　（1）计算第k类样本的协方差矩阵：

　　变化矩阵W的d个列向量由广义特征方程最大的d个广义特征值λ1≥λ2≥…≥λd所对应的广义特征向量w1，w2，…，wd组成，即W=[w1，w2，…，wd]。

　　（5）根据公式Yn=（W*）TXn，计算出训练样本Xn的低维嵌入Yn，其中T表示矩阵的转置，1≤n≤N。

　　1.2 PCA

　　PCA在标准正交变换的基础上进行降维，基本思想是对样本的散布矩阵进行特征值分解。用N表示训练样本的总数，训练样本为（X1，X2，…，Xk，…，XN），映射变化后的低维嵌入维数为d，PCA算法的主要步骤如下[3]：

　　（1）计算所有训练样本的均值向量：

　　（2）计算所有训练样本的协方差矩阵W：

　　（3）计算协方差矩阵W的特征值和特征向量，并对特征值从大到小排序；

　　（4）选择最大的d个特征值λ1≥λ2≥…≥λd对应的特征向量w1，w2，…，wd组成变换矩阵W*，即W*=[w1，w2，…，wd]，根据公式Yn=（W*）TXn，计算出训练样本Xn的低维嵌入Yn，其中1≤n≤N。

　　2 典型非线性降维算法

　　2.1 ISOMap

　　ISOMap算法的基本思想是离得很近的两个点之间的测地线距离用欧氏距离来代替，离得较远的两个点之间的测地线距离用最短路径距离来代替，然后用经典的MDS算法计算出低维嵌入坐标。ISOMap算法的主要步骤如下[10]：

　　（1）构造局部邻域。用N表示训练样本总数，对数据集X={x1，x2，…，xN}计算任意两个样本点xi和xj之间的欧式距离dx（xi，xj），为每个样本点寻找出k个近邻点，将互为近邻的样本点用线段连接起来得到邻接图G。

　　（2）计算最短距离。在图G中，设任意两个样本点xi和xj之间的最短距离为dG（xi，xj）。若xi和xj之间存在连线，则dG（xi，xj）的初始值为dx（xi，xj），否则令dG（xi，xj）=∞。对所有的k=1，2，…，N，根据dG（xi，xj）=min{dG（xi，xj），dG（xi，xk）+dG（xk，xj）}，计算出最短距离dG（xi，xj），最后得到距离矩阵DG={dG（xi，xj）}。

　　（3）应用经典的MDS算法计算出低维嵌入。

　　2.2 LLE

　　LLE算法的基本思想是流形在很小的局部邻域上可以看成局部线性的，可将每个高维数据点用若干个近邻点的线性组合来近似表示，通过计算重构权值矩阵进行降维，将高维流形上的近邻点映射到低维空间。LLE算法的主要计算步骤如下[9]：

　　（1）寻找每个样本点的k个近邻点。

　　（2）定义重构误差min（W）=（xp-wjpxpj）2，其中N表示训练样本总数，xpj表示样本点xp的第j个近邻点，wjp表示重构权值，同一个样本点xj的k个近邻的重构权值的和满足wjp=1。根据重构误差最小原则，利用最小二乘法计算出重构权值矩阵W。

　　（3）根据重构权值矩阵W，计算矩阵M=（I-W）T（I-W）的特征值和特征向量，其中I表示单位矩阵。将特征值从小到大排列，通常取最小的d个非零特征值对应的特征向量作为LLE最终的低维嵌入。

3 实验

　　3.1 数据数据与评价策略

　　为了对比上述4种降维方法的分类性能，采用参考文献[14]中的遥感影像SPOT 5进行分类实验，影像原图和分类参考图如图1所示。实验中选取了4类土地覆盖类型进行分类，分类前先对SPOT 5影像进行多尺度分割。参考文献[15]计算出81维特征。在实验区域中随机选取对象，其中农村宅基地选取了32个对象，河流选取了28个对象，灌溉水田选取了56个对象，养殖水面选取了72个对象。通过2折交叉验证比较4种降维算法的分类性能。

　　ISOMap、LDA、LLE、PCA这4种降维算法只是对训练样本的高维特征进行降维，对于测试样本的低维嵌入应该如何计算，并没有提供有效的解决途径。对于LDA和PCA，本文采用在训练样本的基础上计算得到的映射矩阵计算测试样本的低维嵌入；对于ISOMap和LLE，采用流形学习中经典的Non-parametric mapping[16]计算测试样本的低维嵌入。实验中所采用的分类器为1NN，并根据总体精度（Overall Accuracy，OA）对算法的分类性能进行评估，OA的计算公式如下：

　　其中，N表示训练样本的总数，mkk表示第k类训练样本中正确分类的个数，num表示训练样本的类别总数。

　　3.2 实验结果与分析

　　在ISOMap、LDA、LLE、PCA这4种算法的分类实验中，降维后的特征维数分别取2、5、8、10、15、20、25、30，取这8个结果的平均值作为相应算法在区间[2，30]的平均分类精度。由于近邻个数对ISOMap、LLE算法的分类性能有较大影响，在ISOMap、LLE的实验中重点对比了不同的近邻个数2、4、6、8、10、12对算法性能的影响。对LDA和PCA而言，由于不存在近邻个数，因此在LDA和PCA的分类实验中重点对比了不同归一化方式对算法分类性能的影响。4种算法的分类结果如图2所示。

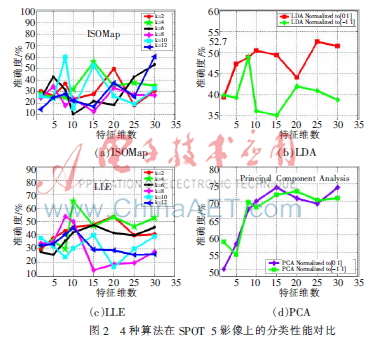
　　ISOMap不同近邻个数得到的分类精度如图2（a）所示。当近邻个数取4时ISOMap的平均OA最高为33.85%，近邻个数取4时的最高OA为55.32%。

　　LDA不同归一化方式得到的分类结果如图2（b）所示。当LDA归一化到区间[0，1]时得到的平均OA为48.01%，最高OA为52.7%；而当LDA归一化到[-1，1]区间时平均OA为40.16%，最高OA为48.94%。很明显，当LDA归一化到[0，1]区间时分类性能会更好一些。

　　LLE不同近邻个数得到的分类精度如图2（c）所示，当近邻个数取4时LLE的平均OA最高为45.22%，近邻个数取4时的最高OA为64.9%。

　　PCA算法不同的归一化方式得到的分类精度如图2（d）所示。当高维特征归一化到[0，1]区间时，PCA的平均OA为66.59%，最高OA为73.99%；而当归一化到 [-1，1]区间时，PCA的平均OA为66.96%，最高OA为72.87%。可以看出，无论是平均OA还是最高OA，两种归一化方式对PCA的分类结果影响并不大。

　　可以看出，就平均OA而言，PCA的分类性能最好，ISOMap算法的OA最低，4种降维算法的平均OA均达不到70%，换句话说，ISOMap、LDA、LLE、PCA这4种算法直接用于监督分类的效果并不好。分析其中的原因，一方面是因为在降维过程中样本的类别标签信息并没有得到充分利用，计算得到的低维嵌入与分类并没有密切的联系；另一方面是因为4种降维算法并没有提供一种有效途径来解决样本外点学习问题。

4 结论

　　本文详细分析了ISOMap、LDA、LLE、PCA这4种降维算法的主要思想和算法步骤并将它们用于有监督分类。在降维过程中，样本的类别标签信息是否得到充分利用会在很大程度上影响到低维嵌入的可区分性。另一方面，样本外点学习问题是降维方法用于有监督分类时必须要妥善解决的一个问题，该问题能否很好解决将在很大程度上影响到降维方法在有监督分类中的应用。

　　参考文献

　　[1] ANIL K J， ROBERT P W  D， Mao Jianchang. Statistical pattern recognition： a review[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000，21（1）：4-37.

　　[2] HUBER P J. Projection pursuit[J]. Annals of Statistics， 1985， 13（2）： 435-475.

　　[3] JOLLIFFE I T. Principle component analysis[M]. Springer， 1986.

　　[4] THOMAS L G， MICHAEL L K. A multidimensional scaling approach to mental multiplication [J]. Memory & Congnition， 2002， 30（1）：97-106.

　　[5] COMON P. Independent component analysis： a new concept[J]. Signal Processing， 1994， 36（3）：287-314.

　　[6] FUKUNNAGA K. Intoduction to statistical pattern recogni-tion[M]. Academic Press， second edition， 1991.

　　[7] Yan Shuicheng， Xu Dong， Zhang Benyu， et al. Graph embedding and extensions：a general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2007， 29（1）：40-51.

　　[8] Yang Jian， ZHANG D. Globally maximizing， locally minimizing： unsupervised discriminant projection with applications to face and palm biometrics[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2007，29（4）： 650-664.

　　[9] ROWEIS S， SAUL L. Nonlinear dimensionality reduction by locally linear embedding[J]. Science， 2000， 290：2323-2326.

　　[10] TENENBAUM J B， SILVA V， LANGFORD J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science， 2000， 290：2319-2323.

　　[11] Lin Tong， Zha Hongbin. Riemannian manifold learning[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2008，30（5）：796-809.

　　[12] Xiao Rui， Zhao Qijun， ZHANG D， et al. Facial expression recognition on multiple manifolds [J]. Pattern Recognition， 2011， 44 （1）：107-116.

　　[13] Huang Hongbing， Hong Huo， Fang Tao. Hierarchical manifold learning with applications to supervised classification for high resolution remotely sensed images[J]. IEEE Transactions on Geoscience and Remote Sensing，2014，52（3）：1677-1692.

　　[14] Qing Jianjun， Huo Hong， Fang Tao. Supervised classification of multispectral remote sensing images based on the nearest reduced convex hull approach[J]. Journal of Applied Remote Sensing， 2009（3）：1-18.

　　[15] Chen Xi， Fang Tao， Huo Hong， et al. Graph-based feature selection for object-oriented classification in VHR airborne imagery[J]. IEEE Transactions on Geoscience and Remote Sensing， 2011， 49（1）： 353-365.

　　[16] SAUL L K， ROWEIS S T. Think globally， fit locally： unsupervised learning of low dimensional manifolds[J]. Journal of Machine Learning Research， 2003（4）：119-155.