摘 要: Hausdorff距离在图像匹配领域广泛应用。针对Hausdorff距离结合一些搜索策略的匹配算法实时性不高的问题,提出了一种基于改进Hausdorff距离和人工蜂群算法搜索策略的图像快速匹配。首先提取模板图像和匹配子图的边缘特征,然后计算的模板图像和匹配子图的Hausdorff距离作为两者的相似度量标准,最后采用人工蜂群算法进行搜索匹配。实验结果表明,该方法在不降低匹配率的情况下,缩短了匹配时间,能应用到嵌入式领域。
关键词: 图像匹配;Hausdorff距离;人工蜂群算法
0 引言
图像匹配[1]是指根据模板图像的特征信息在新的图像中搜索相同或者相似特征信息的子图像过程。图像匹配技术广泛应用于人脸识别[2]、运动目标识别与跟踪[3]、行人检测[4]、图像拼接和融合[5]等领域。图像匹配方法可分为三类:(1)基于图像灰度信息的匹配方法[6]。该类方法易实现,一方面计算量较大,另一方面是当图像信息缺乏时匹配容易失败。(2)基于遗传算法的图像匹配[7]。该类方法完成匹配的概率比一般算法的概率要高,但可能会增加计算量。(3)基于图像特征的匹配方法[8-9]。该类方法计算量小,速度较快,但是对特征信息较敏感。Hausdorff距离是一种常用作图像匹配的相似度量距离参数,它不需要建立两个点集中点的一一对应关系,对图像的噪声和小幅度旋转具有鲁棒性。目前基于Hausdorff距离的图像匹配[10]方法很多,都是以提高匹配速度和匹配率为目的,有些效果并不理想。本文根据人工蜂群算法比遗传算法、差分差异算法在优化问题方面的优越性,以及该算法操作简单、运算快捷的优势来进行图片匹配的搜索,并以改进的部分Hausdorff距离作为相似度量来进行图像匹配。实验结果表明,该算法在匹配率不降低的情况下,减少了图像匹配时间。
1 改进Hausdorff距离
Hausdorff距离[11]是定义在两个点集上的最大最小距离。设两个有限点集A={a1,a2,a3,…,ap}和B={b1,b2,b3,…,bp}。则集合A、B之间的Hausdorff距离定义为:
H(A,B)=max[h(A,B),h(B,A)](1)
其中,‖a-b‖表示点a和b之间的距离范数;h(A,B)表示点集A中所有点到点集B的最小距离的最大值;h(B,A)为反向Hausdorff距离。两者的最大值构成了H(A,B)。
Hausdorff距离表示两个点集之间的相异度。但是传统的Hausdorff距离对集合中的噪声点、异常点特别敏感。针对这种情况,Huttenlocher[11]提出了部分Hausdorff距离。
Hk,l(A,B)=max[hk(A,B),hl(B,A)](2)
其中:
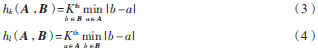
其中,1≤k≤p,1≤l≤q,p、q分别为点集A、B中元素的个数。表示集合A中所有点到集合B中最小距离按从小到大排序后的第K个值,即为hk(A,B)。K值由f和q的积向下取整获取,其中f∈[0,1]。部分Hausdorff能消除噪声和异常点。但是部分Hausdorff距离计算只考虑集合A到集合B的距离,而没有考虑集合A中每一个点到集合B的距离的排序情况,因此部分Hausdorff距离的计算存在一定的误差,可能存在匹配失败的情况。本文根据部分Hausdorff距离提出了一种改进的Hausdorff距离。
设ai是集合A中的一个元素,则ai到集合B的距离为:

其中:k=f·N」,N表示集合A或者B中的个数,f∈[0.6,0.8]。通过平均值来计算dB(a)和dA(b),dB(a)可以有效地避免集合A中ai到集合B的最小距离的计算误差,得到更加符合实际的最小距离,dA(b)同理。则h(A,B)、h(B,A)定义为:
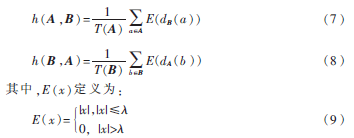
其中,λ是最小距离阈值。当d(x)的值大于λ时,E(x)的值为0。h(A,B)表示集合A到集合B中距离的平均值,h(B,A)同理;T(A)、T(B)分别表示集合A和B中的d(x)≤λ时点的个数。通过平均距离来计算h(A,B)、h(B,A)可以有效地消除样本集中的异常点的影响和抑制样本集中高斯噪声。为了避免集合中仅仅少量点满足最小距离原则,大多数的点被阈值剔除,而Hausdorff距离计算依然满足匹配条件,但是匹配结果是不正确的,因此新的Hausdorff距离计算公式定义为:
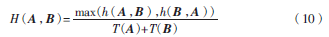
式(10)中考虑了两个集合中有效点的数量,这样当两个集合中的有效点很少或者有不符合常理的相异度时,由于Hausdorff距离的值太多而不再考虑两个集合的相似度的计算。这样可以克服匹配过程中因为噪声、异常点、遮挡和阴影产生的影响。
2 人工蜂群算法搜索策略的图像匹配
2.1 人工蜂群算法简介
ABC[12]是一种群体智能算法,该算法根据蜜蜂采蜜机制来求解最优问题。可将蜜蜂分为侦察蜂、引领蜂、跟随蜂三类。引领蜂和侦察蜂搜寻蜜源,跟随蜂优化蜜源。一只引领蜂对应一个蜜源,寻找到蜜源后释放并标记蜜源信息,跟随蜂根据式(7)选择最大概率处的蜜源为标记蜜源,并根据式(8)在标记蜜源周围搜索新蜜源。新蜜源与标记蜜源进行比较,选取较优异的蜜源反复寻找更优蜜源。若该蜜源经过若干次优化而不能再提高,引领蜂变成侦察蜂,根据式(9)随机搜索新蜜源,直到在该区域中寻找到最优蜜源或者放弃该区域。
设D为优化问题解的维数,蜜源i的随机初始位置为做领域搜索并产生新解。
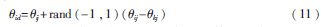
其中,id为新的蜜源位置,ij为蜜源的第j维位置,kj为随机选择的不等于i处蜜源的第j维,rand∈[-1,1]。
设蜂群数量为N,在t次迭代后蜜源位置信息为{xi(t)},i=1,2,…,N。在该次搜索后,得到蜜源的适应为fit(xi(t)),它被选择的概率为:
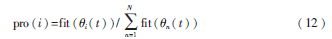
其中,fit(xi(t))就是模板图和待匹配子图的Haursdorff距离的倒数。
设t为?兹i处蜜源最大迭代次数,若某个蜜源i经过t次迭代搜索后没有找到更优质的蜜源,该蜜源被遗弃,同时引领蜂就变为侦察蜂,在整个搜索空间中根据式(9)随机产生一个新解?兹j代替?兹i:

其中,j为新产生的蜜源位置,i为原蜜源位置,?兹k为随机蜜源位置,i不等于k,rand∈[-1,1]。
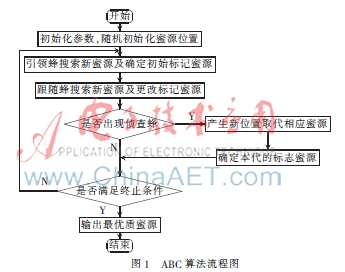
为更直观地描述ABC算法,图1为算法的流程图。
2.2 图像匹配实现步骤
(1)参数初始化。设置蜜源(初始化)个数N,蜜源位置i最大迭代次数t,优化过程最大迭代次数Cycle,蜜源解的维数D,匹配精度的阈值Th等参数的设置。
(2)对模板图像和待匹配图像用中值滤波对图像滤波和用Canny算子作边缘检测,并转换为二值图像,分T和S。二值图像中每个边缘点用坐标位置表示。
(3)为提高匹配速度,将图像S划分为4×5的区域,在每个区域产生一个初始解?兹i,其中i=1,2,…,N。根据式(4)计算T集合和Si集合的HD距离,即fit(xi(t)),并根据HD计算每个解的pro(i)。
(4)根据pro(i)的概率来进行领域搜索,并根据式(8)产生新解?兹id,根据式(7)计算T集合和集合Sid的fit(xid(t)),若fit(xid(t))大于fit(xi(t)),则用?兹id的位置代替?兹i位置,fit(xid(t))的值代替fit(xi(t))的值,否则i、fit(xi(t))保持不变。
(5)若?兹i的位置经过t次迭代搜索而没有被优化,则根据式(9)在S图中随机产生一个新解?兹j代替?兹i。
(6)重复步骤(2)~(5),直到达到匹配的阈值Th或者最大迭代次数Cycle,检测是否达到最优的匹配位置。
2.3 匹配成功与失败判断
设模板图像T在待匹配图像中的起始位置为m(i,j),匹配后的匹配位置为m(i′,j′),根据式(14)计算横坐标和纵坐标的坐标偏差d。
d=‖i-i′‖+‖j-j′‖(14)
根据式(15)判断是否匹配成功。

3 实验结果与分析
3.1 实验结果
为了验证本文的算法,在CPU为Intel(R)Pentium(R)CPU G630@ 2.70 GHz,内存2 GB的硬件设备上用MATLAB2010软件仿真测试。在实验中,f的值为0.65,初始化种群个数N为20,最大迭代次数t为30,最大循环次数Cycle为400,阈值Th为10 000。第一组实验是以ABC为搜索策略,以传统Hausdorff距离(HD-ABC)、部分Hausdorff距离(PHD-ABC)和改进部分Hausdorff距离(SPHD-ABC)作为相似度量进行仿真来测试算法的匹配率;第二组实验是以PHD作为相似度量,分别用逐行搜索的方法(PHD-PS)、遗传算法的搜索策略(PHD-GA)、人工蜂群算法的搜索策略(PHD-ABC)进行仿真来测试算法的搜索策略,每种算法进行30次仿真测试。
3.2 实验结果分析

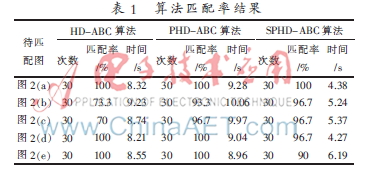
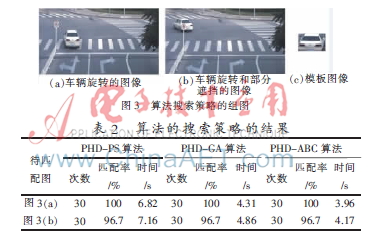
本文实现了两组对比实验。第一组实验测试了在ABC搜索策略不变的情况下,分别以HD、PHD和SPHD作为相似度量进行仿真实验。图2中(a)到(f)图分别为基准图、加入高斯噪声的基准图、加入椒盐噪声的基准图、缩放10%比例的基准图、顺时针旋转10°的基准图、g为匹配模板图。算法匹配率如表1所示。由表1结果可看出,HD-ABC算法在图像中加入高斯噪声和椒盐噪声的情况下匹配率较低,其他情况下匹配度较高。但是该方法的平均匹配时间较长,无法满足实时性要求。PHD-ABC算法和SPHD-ABC算法在图像中存在各种变换的情况下的匹配率相当,但是SPHD-ABC算法平均匹配时间少于PHD-ABC算法的平均匹配时间。第二组实验测试了以PHD作为相似度量标准,分别用逐行搜索的方法(PHD-PS)、遗传算法的搜索策略(PHD-GA)和人工蜂群算法的搜索策略(PHD-ABC)进行仿真测试。图3中(a)图为旋转的基准图、(b)图为部分遮挡和旋转的基准图、(c)图为匹配模板图。算法的搜索策略对比结果如表2所示。由表2可以看出,在相似度量准则相同的情况下,三种搜索策略的匹配率基本相同,但是以ABC为搜索策略平均匹配时间远远小于逐行搜索平均匹配时间和优于GA为搜索策略的平均匹配时间。
4 结论
部分Hausdorff距离在图像匹配方面作为相似度量标准得到广泛应用。同时,ABC在求解最优问题具有计算简单,收敛时间短的优势。本文提出的简化部分Haursdorff距离的计算方法将简化的部分Haursdorff距离作为相似度量准则并结合人工蜂群算法的搜索策略,实现了图像匹配。实验结果表明,在图像存在高斯噪声、椒盐噪声、部分遮挡、小幅度旋转的情况下,本文算法的平均匹配率不低于其他算法平均匹配率,但是平均匹配时间小于其他算法的平均匹配时间,增加了实时性的需求。该算法可移植应用到嵌入式系统中。但是,人工蜂群算法在图像匹配中也存在局部最优的问题,这需要进一步研究。
参考文献
[1] 熊凌.计算机视觉中的图像匹配技术[J].湖北工业大学学报,2003,21(3):171-173.
[2] 刘福新,杜世培,陈益强.基于改进Hausdorff距离的人脸匹配方法[J].计算机工程与应用,2007,43(35):169-171.
[3] 刘玉秋,王康平,刑玉梅.视频流中的自适应阈值模板匹配车辆检测算法[J].吉林大学学报,2007,45(5):791-794.
[4] 万力,武爱民.基于Hausdorff距离的行人跟踪计数方法[J].信息技术,2007(8):105-107.
[5] 庄志国,孙惠军,董继扬.基于角点检测的图像匹配算法及其在图像拼接中的应用[J]. 厦门大学学报(自然科学版),2007,46(4):501-505.
[6] 王振江,吴健,林方全.一种结合快速灰度投影与SSDA的图像匹配方法[J].计算机工程与应用,2011,47(33):195-197.
[7] 黄涛,杨华高,胡水才.遗传算法在相关匹配中的应用研究[J].舰船电子工程,2010(3):70-72.
[8] Zhou Ji, Shi Jiaoying. A robust algorithm for feature point matching[J] .Computers &Graphics, 2002;26(3):429- 436.
[9] 刘佳,傅卫平,王雯,等.基于改进SIFT算法的图像匹配[J].仪器仪表学报,2013;34(5):1117-1111.
[10] 高晶,孙继银,刘婧.基于邻域灰度信息的Hausdorff距离图像匹配方法[J].计算机应用,2011;31(3):741-744.
[11] HUTTENLOCHER D P, KLANDERMAN G A, RUCKLIDGE W J. Comparing images using the Hausdorff distance[J]. IEEE Transactions on Pattern Analysis and machine Intelligence,1993,15(9):850-863.
[12] KARABOGA D, BASTURK B. On the performance of artificial bee colony algorithm[J]. Applied Soft Computing, 2008,8(1):687-697.

