摘  要： 随着社会网络数据的增加，社团发现获得来自学术界和工业界的大量关注，是因为它在现实世界中有许多的实际应用。格文-纽曼（Girvan-Newman，GN）是现今最流行的算法之一，但在大型网络上由于需要计算网络中每对节点之间的最短路径而产生了相应的局限性。为此，利用MapReduce模型，提出了一种并行版本的GN算法来支持大规模网络的新方法，称之为最短路径之间的MapReduce算法（Shortest Path Betweenness MapReduce Algorithm，SPB-MRA）。此外，还提出了一个近似技术，进一步加快社区检测过程。在Hadoop上利用开源平台MapReduce框架实现了SPB-MRA算法。结果表明，随着reducer数量的增加时间呈线性减小，并且引入了一种近似技术可以忽略误差。

　　关键词： Hadoop；MapReduce；社区检测；GN算法；SPB-MRA

0 引言

　　社会网络服务（SNS网站），如Facebook和Twitter，在实际生活中变得越来越流行。因此分析社会网络数据就成为各领域面对的最重要的问题之一。在这些分析工作中，社会网络数据的社团发现在社会生活中有着实际的应用，因此获得来自学术界和各行业的广泛关注。由格文和纽曼[1]提出格文-纽曼（GN）算法引入边介数的概念，用来衡量中心性和网络中边缘的影响度。虽然GN算法被广泛应用，但当它支持大型网络时，由于需要计算每对节点之间的最短路径而具有局限性，而且节点对的数量也是有限制的。在大数据时代，可用的数据量空前增长，因此，数据分析是一种良好的可扩展方法，可以用来处理大型数据集。MapReduce是一个用于处理大数据集的并行编程模型，分布式聚类算法在MapReduce中可扩展性和易于使用的性质[2-4]而得到广泛的应用，这也是近年来在背后驱动分析大数据的动力。本文提出了一个并行版本的GN算法，即SPB-MRA算法来支持大规模的网络，并且提出了一种近似技术来进一步加快社区检测过程。

1 背景

　　1.1 MapReduce和Hadoop[5]

　　MapReduce并行的方式是一个加工大规模数据的编程模型[2]。用户可以轻松地通过编写map和reduce两个函数实现分布式并行处理的功能。map函数处理数据输入和键值对<key，value>，reduce函数是把具有相同key的value值进行合并后输出。

　　1.2 GN算法

　　GN算法是分裂的分层聚类算法，利用边界数[1]的概念。在提出的三种计算边界数的方法中计算最短路径的结果是最好的。边界数是指经过两个节点之间的最短距离的值。由于社团是由一些“组间”边界松散地链接而成的，在不同社团之间所有最短路都必须经过这些“组间”边，这些边连接起来的社团的边界数将会很大，因此，社团可以通过不断检测来排除这些边。从每对节点中最获得最短路径，所以GN算法的代价是非常高的。

2 算法

　　SPB-MRA经历了4个并行计算的阶段，每个阶段执行自己的map和reduce任务。在每次迭代中，第一阶段会执行多次，而其他阶段只执行一次。运行这4个阶段直到结果的质量不再有所改进。在社团发现中每对节点由7个元素组成的元组构成，元组中包含网络结构（例如邻接表），这时最短路径通过元组获得。

　　targetid表示一个目的节点的最短路径且最初设置为sourceid。sourceid表示最短路径源节点且最初设置为targetid。distance表示最短路径的长度，初值为0，每次迭代过程中更新第一阶段的distance值。status表示一个特定的路径的状态。a表示积极的（active）；i表示不积极的（inactive），意味着最短的路径已检测到。weight表示从sourceid到targetid最短路径的数目且最初设置为1。pathinfo表示最短路径经过的节点的列表，初始值为空。adjlist表示targetid中相邻的节点的列表。

　　2.1 第一阶段：找到所有节点对之间的最短路径

　　在第一阶段，采取Zeng Zengfeng等人[6]提出的由一种多源消息传递模型的方法来计算每对节点之间的最短路径。在map阶段中输入一个元组，若它的status是i，无需后续操作；若status是a，则改成i，距离加1并将targetid增加到pathinfo中；该元组被送到reduce阶段。通过给在邻接表中的每个点分配targetid即可生成新的元组。这些新生成的元组其status被设置为a，邻接表被设置为空，并且其他元素被设定为那些发送前的元组的状态，如图1所示。

　　2.2 第二阶段：计算边界数

　　在第二阶段，计算网络中每对节点之间的边界数。在map阶段，整体根据最短路径的sourceid和targerid的数目（即权重）被划分成某条最短路径上的边。在reduce阶段，每个边由每个最短路径的分量相加得到，如图2所示。

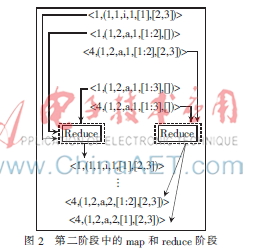
　　2.3 第三阶段：选择要删除的边缘

　　在第三阶段，kiter边按边界数选择。kiter是由用户作为调节参数而指定的。在map阶段，不需要进行后续操作。在reduce阶段，边按照边界数的递减顺序排序，并且top-kiter边缘被选定。只要运行一个reducer即可得到一个整体的排序结果，如图3所示。

　　2.4 第四阶段：删除边

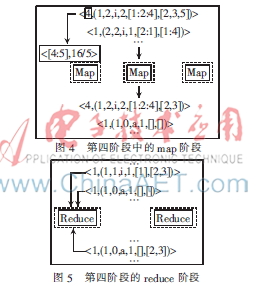
　　在第四阶段，把网络中在第三阶段选择的边删除，但在下一次迭代中，一个新的元组集合的生成表明需要重新计算删除边的边界数。注意，如果一个最短路径包含被去除边，边界值就会改变，那么边界数将会发生变化。在map阶段，如果第二阶段分组中的targetid影响到第三阶段边缘的选择，如果删除相应节点来表示新的网络结构，则它的邻接表就会更新，其他的元组在下一次迭代中初始化，如图4所示。在reduce阶段，在邻接表里的元组都会有一个更新的值，这些元组将作为下一次第一阶段中的输入而提供数据，如图5所示。

3 性能试验

　　3.1 数据和环境

　　采用来自于Stanford Large Network Dataset Collection[7]上的ca-GrQc和ca-HepTH两组数据集，使用Java 1.6.0和Hadoop 1.0.4实现SPB-MRA。在亚巴逊弹性计算（Amazon EC2）利用m1.xlarge进行性能测试。Amazon EC2是由亚马逊公司提供的Web服务，用户可以租用其云电脑运行时所需要的相应系统。

　　3.2 可扩展性

　　为了显示SPA-MRA的可扩展性，经过一次迭代的同时reducer的数量从1变为32，结果如图6和图7所示。

　　随着reducer的数量增加到8，所用的时间呈线性减少。对于这些数据集来说，reducer的数量是足够的，过多的reducer就会变得无效。可以看出，CA-HepTh数据集的大小是CA-GrQc数据集的两倍，而图7中的曲线要比图6中的曲线率先变得平缓。

　　为了显示SPA-MRA近似值的精度，在不同的kiter值下测量F-score[8]的值，如表1所示。其中，kiter表示一次迭代中要删除边缘的数量。在表1中，虽然一次性删除40条边F-score值只减少了10%，但是它证明4次提速却只有10%的误差。

4 结论

　　本文提出了一个并行版本的GN算法即SPB-MRA来支持大规模的网络，并利用MapReduce模型在Hadoop平台上得到了实现。在亚马逊的EC2上进行了实例SPB-MRA性能试验，结果表明，随着reducer数量的增加时间呈线性减少，并且逼近值技术的错误率可以忽略不计。未来的工作是进一步提高SPB-MAR的性能，引入额外的近似技术。

参考文献

　　[1] NEWMAN M E， GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E， 2004，69（2）：026113-1-026113-15.

　　[2] DEAN J， GHEMAWAT S. MapReduce： simplified data processing on large clusters[C]. Communications of the ACM， 2008，51（1）：107-113.

　　[3] CHAIKEN R， JENKINS B，  LARSON P.-A°， et al. Scope： easy and efficient parallel processing of massive data sets[C].Proceedings of the VLDB Endowment， 2008，1（2）：1265-1276.

　　[4] COHEN J， DOLAN B， DUNLAP M， et al. Mad skills： new analysis practices for big data[C]. Proceedings of the VLDB Endowment， 2009，2（2）：1481-1492.

　　[5] Hadoop Apache. Software Foundation.(2013-08-01）[2014-07-01].http：//hadoop.apache.org.

　　[6] Zeng Zengfeng， Wu Bin， Zhang Tiantian. A multi-source message passing model to improve the parallelism efficiency of graph mining on MapReduce[C]. Proceedings of 2012 IEEE International Parallel and Distributed Processing Symposium Workshops & PhD Forum（IPDPSW），2012：2019-2025.

　　[7] Stanford large network dataset collection[EB/OL].[2013-08-01]. http：//snap. stanford.edu/data.

　　[8] Han Jiamei， KAMBER M， Pei Jian. Data mining： concepts and techniques（2nd edition）. Morgan Kaufmann， 2006.