0 引言

    正交频分复用（OFDM）技术克服了频率选择性衰落以及无线信道的多径效应，并引入了无线蜂窝系统的中继站（RS），可以增加覆盖范围，提高抗衰落能力，并降低系统的功率消耗。中继技术主要包括放大转发中继技术以及解码转发中继技术，基于放大转发和解码转发中继的OFDM系统可以根据用户的QoS需要进行中继选择，进行自适应功率分配，以达到最小能耗^[1]。本文根据OFDM调制对于频率选择性信道考虑了功率的分配，使用DF选择性中继进行子载波选择配对及功率优化分配。

    黄高飞等^[2]提出一种具有时延QoS保证的OFDM中继系统子载波配对与功率分配算法，在满足业务时延QoS要求的前提下最大化系统容量，并将子载波配对与功率分配问题形成混合整数规划问题,利用凸优化方法得到原问题的最优解，有效地提高系统容量。陈煜[3]等提出一种基于能效的解码转发中继OFDM链路自适应功率分配方案，分析了速率和功率限制对能效的影响，基于解码转发(DF)中继OFDM频率选择性链路，提出最优能效功率分配方法，在保证较高速率的同时获得最好的系统能效。赵晓晖等[4]提出一种多中继OFDM系统选择性子载波中继和功率分配算法，利用空闲中继节点的功率，提高系统容量，并通过削减中继节点数目，在降低系统复杂度的同时提高功率效率。Gaofei Huang等[5]提出了统计质量的服务（QoS）保证的资源分配方案，用于无线OFDM放大转发（AF）中继系统，首先制定了无线OFDM的AF中继系统具有QoS保证的非凸问题以及资源分配问题，然后通过定义OFDM的AF中继系统的适当的放大器增益，把非凸问题转化为凸的问题，从而提出了次优的资源分配方案。Qingtao Wan等[6]提出一种解码和转发的OFDM中继系统异构服务的资源分配算法，该算法旨在最大化非实时服务（NRT），同时满足实时服务（RTS）要求的数据速率，将要解决的问题分解成RTS和的NRT的功率分配两个子问题。通过拉格朗日方法解决RTS问题，通过一种两步算法解决NRT问题。

1 系统模型与问题描述

    无线OFDM网络在频率选择性信道上运行，源端希望在中继的协助下将数据发送到目的地，假设信道的带宽?追被划分为N个副载波，并且一个传输周期持续两个时隙^[7]，定义在信号源和目的地之间的第i个副载波的信道增益为SD_i，信号源和中继之间的第i个副载波的信道增益为SR_i，中继和目的地之间的第i个副载波的信道增益为RD_i。假设在时隙期间这些信道增益不会改变^[8-9]。在第一时隙，数据在所有子载波上是通过信号源广播到中继和目的地，采用的功率为P_S，1；在第二时隙，在M个副载波上被选择用于中继译码、变换，并采用功率P_R转发数据；在其余的副载波上，信号源采用功率P_R发射新的数据。因此，对于一个给定消息中继可能会使用不同的副载波作为使用的一个来源。

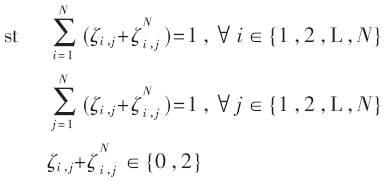
2 子载波选择配对

    配对和选择等同于确定最佳的H_R和矩阵，这是一个整数规划问题，本文采用了基于匈牙利算法的规划方法。

    首先，定义矩阵：

3 功率优化分配的OFDM系统

    将目标函数式（9）分成两个子问题^[10]：

    子问题1：

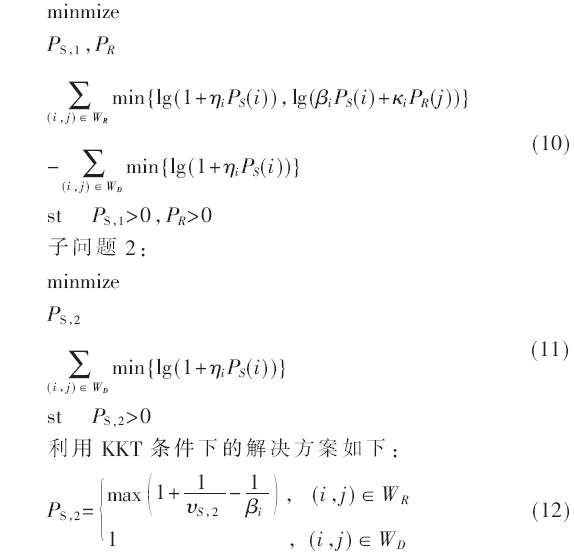
其中ν_S，2表示PS_，2的约束值。

    由于目标函数是一个求和凸函数，并且约束是针对仿射和线性问题^[10]，因此可以采用两个步骤来解决问题。

    第1步：设置电源功率是恒定的并且通过KKT条件来优化中继功率：

    最后，这两个步骤可以交替进行，直到达到收敛。该方法能快速收敛到最佳点。

4 实验仿真结果

    对本文算法所选择的DF子载波配对和功率优化分配方法所表现出的性能，通过模拟在不同的源节点与中继节点距离、中继节点与目的节点距离以及不同的源节点与中继节点功率预算下的实验情况来进行验证，假设源节点和目的节点的距离保持不变，为1 000 m，并且中继节点的位置由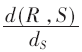表示，d_S表示初始距离，d(R，S)表示中继节点与源节点的距离。定义OFDM调制的子载波数为N=20，子载波的间隔为10 kHz，并且Ψ_R=Ψ_D=4.0×10^-17，信道复增益采用下面的分布规律从瑞利衰落信道获取：

    其中，d表示距离，路径损耗指数n=4，阈指数F=3。

    为了验证提出的基于子载波选择配对及功率优化分配的OFDM系统在提高网络覆盖率上的性能，在实验中与文献[5]的统计质量的服务（QoS）保证的资源分配方案以及文献[6]的OFDM中继系统异构服务的资源分配算法进行了对比。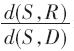表示源节点与中继节点的距离相比源节点与目的节点的距离的比值。从图1中可以看出，在比值为0.6左右算法的迭代过程收敛到最优解，本文提出的算法的网络覆盖率达到了92%，而文献[5]算法则为85%，文献[6]算法为83%，因此本文的方法在提高网络覆盖率上表现出了更加良好的性能。

    考虑到OFDM系统子载波选择配对以及功率优化分配下网络容量的提升效果，以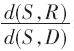作为变量，通过实验仿真得到了算法的网络容量测量结果。从图2中可以看出，处在源节点与目的节点之间的中继节点，其位置的变动会影响到网络容量大小，因为中继节点承担着数据的解码和转发任务，并且影响着子载波的选择配对。图中当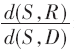接近于0.7时，算法的网络容量达到最大，之后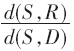的值增大时网络容量开始逐渐减小。本文算法的网络容量最高达到了2.13 B/s/Hz；文献[5]最高达到了1.57 B/s/Hz，仅为本文算法的74%；文献[6]的网络容量最高达到1.78 B/s/Hz，仅为本文算法的84%。

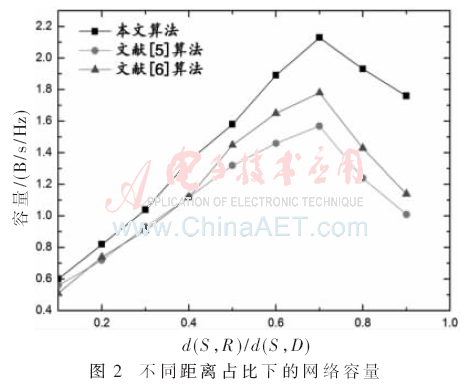
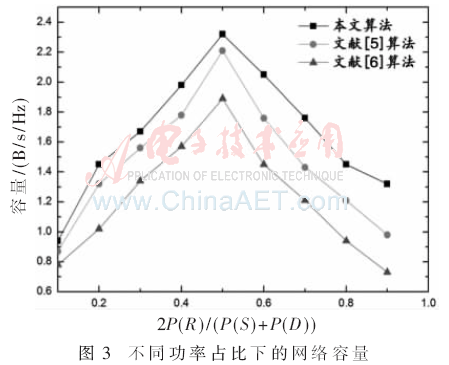
    图3显示了在不同的功率分配情况下算法所得到的网络容量，P(R)表示中继节点分配的功率，P(S)、P(D)分别表示源节点和目的节点分配的功率，以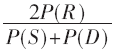作为横坐标，以网络容量作为纵坐标，得到了图3的结果。从图3中的数据分布情况来看，的值接近于0.5时网络容量达到最大，其中本文算法的网络容量为2.32 B/s/Hz，文献[5]为2.21 B/s/Hz，文献[6]为1.89 B/s/Hz，且在比值变化的过程中本文算法的网络容量相比这两种对比算法来说仍然占据优势。根据图2和图3的结果可知，本文提出的OFDM系统在提高网络容量上具有更好的性能。

5 结论

    本文提出了一个OFDM协作通信系统的子载波选择性配对及功率优化算法，该算法根据系统模型进行中继配对联合优化及功率分配分析，采用基于匈牙利算法的规划方法进行子载波选择配对，在功率分配上通过将目标函数转换为一个求和凸函数，并利用KKT条件来优化中继功率。实验中使用了类似的解决方案及算法进行对比，从数据分析的结果来看，本文提出的算法在提高网络覆盖率和网络容量上优于其他方法。在今后的工作中，将针对OFDM协作通信系统的功率消耗问题展开进一步研究，尽可能地减少OFDM协作通信系统的能量消耗。

参考文献

[1] NAVARRO-ORTIZ J，AMEIGEIRAS P，LOPEZ-SOLER J M，et al.A QoE-aware scheduler for HTTP progressive video in OFDMA systems[J].IEEE Communications Letters，2013，17(4)：677-680.

[2] 黄高飞，罗丽平，张广驰，等.具有时延QoS保证的OFDM中继系统子载波配对与功率分配算法[J].电子学报，2013，41(2)：335-339.

[3] 陈煜，方旭明，赵越.基于能效的解码转发中继OFDM链路自适应功率分配方案研究[J].电子与信息学报，2013，35(2)：285-290.

[4] 赵晓晖，杨伟伟，金晓光.多中继OFDM系统选择性子载波中继和功率分配算法[J].吉林大学学报(医学版)，2013，44(1)：478-484.

[5] HUANG G，ZHANG G，ZHENG H，et al.QoS-driven resource allocation scheme for the OFDM amplify-and-forward relay system[C].Wireless Communications，Networking and Mobile Computing(WiCOM)，2011 7th International Conference on.IEEE，2011：1-4.

[6] WAN Q，MA G.Resource allocation algorithm for heteroge-neous services in decode-and-forward OFDM relay system[C].General Assembly and Scientific Symposium，2011，URSI.IEEE，2011：1-4.

[7] KOSHIMIZU Y，OKAMOTO E.An efficient channel estimation scheme using Walsh pilots in bi-directional wireless OFDM relay systems with analog network coding[J].IEICE Transactions on Communications，2013，96(8)：2119-2130.

[8] SIMMONS D，HALLS D，COON J P.OFDM-based nonlinear fixed-gain amplify-and-forward relay systems：SER optimization and experimental testing[C].Networks and Communications(EuCNC)，2014 European Conference on.IEEE，2014：1-5.

[9] SHAH R A，RAJATHEVA N，JI Y.Analysis of BER and capacity for dual-hop OFDM relay system with subcarrier mapping in Nakagami-m fading[C].Communications(ICC)，2014 IEEE International Conference on.IEEE，2014：5089-5094.

[10] HASAN Z，BHARGAVA V K.Relay selection for OFDM wireless systems under asymmetric information：a contract-theory based approach[J].IEEE Transactions on Wireless Communications，2013，12(8)：3824-3837.