0 引言

　　体感技术是指通过做出肢体动作而无需操作任何复杂的控制设备就可以身临其境的人机互动技术[1]。区别于按键与触摸等传统的交互方式，体感技术提升了操作的灵活性、直观性，在游戏、移动应用、运动康复、虚拟学习系统等领域中，有着越来越广泛的应用[2-5]。

　　目前的体感机械臂控制算法中，对于人手臂与机械臂姿态之间的映射，主要是基于几何关系求其运动学正反解[6]，其核心思想是进行线性映射，令机械手臂完全模仿人的手臂姿态。而人体手臂构造与机械不同，手臂的生理结构决定了其不具备机械关节那样完全的自由度[7]，而且考虑到力度、能量消耗等因素，手臂做出不同动作的难易程度也不尽相同。这就导致在操作机械手臂完成一系列动作的过程中操作者容易疲劳，效率较低，不能长时间作业。

　　为了减轻使用者的疲劳度，提高控制的舒适性和效率，考虑人手臂的舒适程度以及能量消耗等因素的影响，提出一种基于映射关系的体感机械臂舒适控制算法。

1 系统设计

　　1.1 总体设计

　　设计了机械臂体感控制系统，总体分为运动采集模块、机械臂控制模块、机械臂运动模块三部分，如图1所示。

　　运动采集模块采集人手臂的姿态信息，经过姿态解算和无线传输到达主控制器，通过舒适控制算法的处理，实现从手臂姿态到机械臂动作之间的映射，令机械臂的肩、肘以及腕关节处的舵机转到目标角度，实现体感控制机械臂。

　　1.2 机械臂系统设计

　　为减少加工机械臂结构所消耗的时间和成本，利用博创机器人套件的舵机及其可组装散件，搭建了五自由度刚性机械臂，并以人肩部为原点建立手臂平面坐标系，如图2所示。分析体感姿态用到了运动学正反解算法，采集手臂角度α、β，解算后映射到右侧机械臂的五个关节处舵机转角（图1中①~⑤），实现机械臂定位。

　　基于惯性体感技术，设计了一种集成MPU6050陀螺仪模块、24L01无线发射模块和STM32单片机于一体的小型可穿戴式无线姿态监测模块，通过通信组网，将实时采集到的姿态信息经运算处理传回主控制器。

　　1.3 算法设计流程

　　依据现有疲劳度理论，结合体感机械臂控制实验，为人手臂较为舒适的控制区域建立空间模型。用体感机械臂装置做大量样本实验，实测舒适区域的样本，与理论计算结果比对，用数学方法拟合并确立舒适空间。以测得的手臂舒适区域作为反馈，进一步优化和改进算法，修正动作映射关系，最终确立舒适控制算法。

2 舒适空间预测

　　舒适是一个模糊的概念，目前尚无公认的量化指标，但仍有一些研究成果可以借鉴。通过理论分析和计算得出量化指标，进而分析舒适度情况。

　　结合体感舒适性相关领域研究[8-10]，可以推测人手舒适范围应具备以下特征：舒适度范围可能与手臂运动角度、方向以及速度有关；为了简化计算，取速度为60°/s，结合体感机械臂控制实践，考虑手臂肘关节的伸展和弯曲两个方向（对应于坐标系中y轴运动），肩关节的内曲和外展方向（对应于坐标系中x轴运动)计算舒适度，绘出的满足舒适性条件的直角坐标形式如图3所示。

　　结合计算结果分析可知，在假定简化模型的条件下，手臂的舒适控制区域偏坐标系左下方，成椭球形。为了进一步确定手臂的舒适控制区域，设计了让实验者以下臂自然平举正前方为圆心，画最大圆以获得感性最大舒适区，实验结果如图4所示。经分析可发现整体趋势与理论计算相仿，舒适区域偏向于坐标系左下方。这为后续样本实验提供了有利的参考。

3 测定舒适范围

　　为保证上述理论在模型建立与算法设计过程中具有指导意义，设计了A、B两组实验，分别定量测试了径向平面ρoz内和ρ=C(常数)的圆柱曲面内的手臂舒适范围。系统抽样了习惯使用右手的30名同学作为被测者，穿戴姿态监测模块根据自身习惯与控制舒适程度做出一系列规定的控制指令，将所有动作采集后汇总分析。

　　3.1 实验A(径向测试实验)

　　测量了操作者的手腕在ρoz平面内运动时舒适区域的分布情况。实验设定了9个典型机械手位置，请被测者按照操作意愿为其制定最舒适的控制动作，通过测量与姿态解算后，得到如图5所示的控制姿态示意图。

　　实验得出以下三点结论：

　　(1)除特殊动作(需要控制机械臂举高、伸直等)外，手腕位置近似维持在以肩部为顶点，锥角为60°的圆锥锥面内，距离肩部距离最远的位置约为伸直状态下的9/10，最近位置约为伸直状态下的1/3，如图6所示。

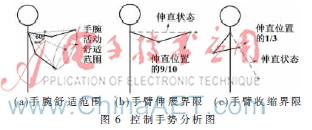
　　(2)当手腕处在舒适活动范围内（锥面内）时，人手下臂方向与机械臂的五号关节、三号关节所连线段方向平行，且人手腕到肩部的距离近似与五号关节、三号关节之间距离成正比。此结论说明当手臂在舒适范围内时，人对机械臂的控制意愿更倾向于线性映射。

　　(3)当手腕处在不太舒适的位置（锥面外）时，例如控制机械手举高，操作者总是希望自己的手不至于举得太高（会过于疲劳）就可以控制机械臂举得比较高，所以设计算法时应该在人手不舒适的范围设置更高的控制灵敏度，以减轻人手臂负担。此结论为在ρoz平面内建立映射关系提供了参考。

　　3.2 实验B(点阵指定实验)

　　实验测量了操作者的手腕在一个与轴线距离为常数C的柱面内运动时舒适区域的分布情况。

　　由于舒适范围集中在一个锥角为60°的锥面内，柱面被该锥面切割剩余部分弧度不大，实验中可近似认为平面来处理。设计了同一平面内的5×5点阵，平均分布在机械手前方能够触及到的区域。按照一定顺序指出一系列点，请被测者按照控制意愿将手腕跟踪到每一个对应的位置，记录手臂姿态。做出每个动作后将手自然下垂短暂休息，减小疲劳度对测试的影响。

　　每位被测者按照不同点描绘出的轨迹做出动作汇总，绘制折线图。分析位置关系可知，折线中相邻两节点间距离越小，表明操作者为机械手制定的操作姿态在该范围内变化幅度越小，说明该区域就越远离舒适范围。

　　综合实验得出结论：手臂舒适范围在柱面内近似体现为椭圆形，其长轴与水平方向所成角度约为45°。其中水平扫描动作的位置记录图如图7所示。

4 算法设计与验证

　　实验结果表明，通过实际测量得出的手臂舒适范围与理论推导的舒适范围基本吻合，尤其在分布范围的形状以及分布形态的方向与预期差别不大时，这说明可以根据实验验证和理论计算结果分析推导出适合的舒适算法。

　　4.1姿态映射算法设计

　　由于控制方式为体感，不可避免会随人的主观意识产生误差，在总体趋势正确并在合理误差范围内可以认为测试数据可信。在误差允许的情况下，可以依据此方法建立控制模型。归纳整理控制动作与目的位置之间的关系可以得出：当手臂在舒适范围内时，人对机械臂的控制意愿更倾向于线性映射；在舒适范围外时，人手控制动作幅度会变小。

　　所以在对映射算法改进时，可以对舒适范围建立模型，将范围的边界作为分段条件，将控制动作分段处理：如果判定手腕在此范围内，则将手部动作线性映射到机械手的动作空间；当手腕在此范围之外时，使控制灵敏度提高，在发出控制指令时乘以一个大于1的比例系数K，将小幅度的姿态映射到较大幅度的控制空间。

　　设在θ方向，舒适范围的中心点与手距离为mθ，与舒适范围最远点距离为nθ，则在θ方向上，K值大小与超出舒适范围程度（mθ-nθ）/nθ呈正相关。

　　这里近似满足椭圆中点到椭圆各点的距离关系，用斜椭圆方程界定了舒适范围：

　　x为手腕舒适范围曲面近似成的平面内的水平坐标，用弧长表示，即x=L·θ，y为手腕高度，即y=z0，(x，y)表示手腕的坐标，θ是椭圆长轴与水平方向夹角，取45°。为了保证当手匀速移出舒适范围时机械臂动作的平滑度，在分段点（mi-ni=0）外侧比例系数曲线斜率应该为零。本方案中K取值满足：

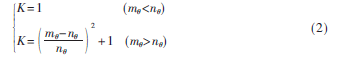
　　最后采用运动学反解算法，使机械臂完成相应动作。

　　4.2 算法的测试与验证

　　改进映射关系后，利用新算法对映射关系进行验证，得到如图8所示验证结果。比较两种算法的实验结果，被测试者疲劳度减少51.8%，同时测得控制精度达到2 mm，空间定位准确率为95.4%。

5 结论

　　实验证明改进后的映射关系能够保证机械手准确地按照控制指令完成动作，有效改善舒适程度。算法改进后，大部分被测者能够轻松舒适且准确地控制机械臂完成一些复杂的、有技巧的动作，例如抓取小球并放置于瓶盖上，疲劳程度比传统体感算法更低。

　　本文基于现有的人机工程学研究成果，考虑肌力和能量利用率与疲劳度之间关系，结合人手臂的舒适活动范围，遵循能量利用率尽可能高、肢体动作尽可能舒适的原则，通过仿真与实验分析考证了各个因素对控制结果的影响，最终建立了一种控制动作与目标动作之间的映射关系，并提出了机械臂舒适控制算法，有效提高了体感控制机械臂的舒适性，让体感控制更加人性化。

参考文献

　　[1] 郑杨硕，方兴.信息交互方式的历史演进研究[D].武汉：武汉理工大学，2013.

　　[2] 廖宏建，杨玉宝.体感交互设计及其在三维虚拟实验中的应用[J].远程教育杂志，2013(1)：54-59.

　　[3] 代艾波，瞿畅，朱小龙，等.体感交互技术在运动康复领域的应用[J].中国康复理论与实践，2014(1)：41-45.

　　[4] 王俊杰，王培勇，徐坚，等.体力活动干预新方式：体感游171-177.

　　[5] 庄翠翠，李成荣，韦玮，等.基于Android系统的多传感器移动体感应用[J].计算机系统应用，2013(8)：72-75.

　　[6] 李宪华，郭永存，张军，等.模块化六自由度机械臂逆运动学解算与验证[J].农业机械学报，2013，44(4)：246-251.

　　[7] JOVANOVIC V T，KAZEROUNIAN K．Using chaos to obtainglobal solutions in computational kinematics[J]．Journal of Mechanical，1998，120：299-304．

　　[8] 王睿，庄达民.基于舒适性分析的舱室手操纵装置优化布局[J].兵工学报，2008，29(9)：1149-1152.

　　[9] 郑秀瑗，贾书惠，高云峰，等.现代运动生物力学[M].北京：国防工业出版社，2002：363-369.

　　[10] 钱东海，王新峰，赵伟，等．基于旋量理论和Paden-Kahan子问题的6自由度机器人逆解算法[J]．机械工程学报，2009，45(9)：72-76．