文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.10.028
中文引用格式: 陈琳,严迎建,周超,等. ECC处理器时间随机化抗DPA攻击设计[J].电子技术应用,2015,41(10):103-106.
英文引用格式: Chen Lin,Yan Yingjian,Zhou Chao,et al. The design of anti-DPA attack with time randomization for ECC processor[J].Application of Electronic Technique,2015,41(10):103-106.
0 引言
椭圆曲线密码(Elliptic Curve Cryptography,ECC)[1]的算法安全性是建立在解椭圆曲线离散对数数学难题之上的,是目前公开密钥密码中单位比特长度安全性最高的密码算法[2]。但是当密码算法在硬件实现时,其安全性不仅依赖算法和协议的安全性,还要依赖实现的安全性。能量分析(Power Analysis,PA)[3]攻击通过分析密码设备工作时的能量消耗来获取密码算法的秘密信息,避开了求解数学难题,对密码系统的安全造成了很大威胁。能量攻击主要分为简单能量(Simple Power Analysis,SPA)[4]攻击和差分能量(Differential Power Analysis,DPA)[5]攻击。其中DPA攻击是利用密码设备能量消耗对数据的依赖性,利用统计分析手段分析固定时刻设备的能量消耗,进而获取运算过程中的秘密信息,成为最具威胁的能量攻击手段,因此有必要对密码设备进行抗DPA攻击设计。
时间是影响DPA攻击的重要因素,DPA攻击之所以能够成功,是因为密码设备每次执行的相应运算操作都会出现在固定的时间点上,因此可以从时间角度对密码设备进行抗DPA攻击设计。时间随机化通过在密码设备运行过程中插入随机时间延迟,扰乱功耗与操作和数据的关系,使统计分析手段失效,进而达到抗DPA攻击的目的。目前常用的时间随机化技术主要有多时钟技术[6]、门控时钟延迟技术[7]、冗余指令延迟等,其中多时钟技术要求系统中有多个时钟源,并且会增加系统的控制复杂度;门控时钟延迟技术产生的随机延迟部分表现在能量迹上为一段直线,很容易被区分剔除;由于ECC处理器的运算指令为多周期指令,且不同指令的周期不同,导致时间延迟的基本粒度较大,不利于控制。
针对上述问题,本文在分析了时间随机化抗能量攻击原理的基础上,结合ECC处理器的处理特点,有针对性的设计了基于软中断的可配置时间随机化抗DPA攻击电路,并对其进行仿真分析,结果表明本文设计的时间随机化电路能够达到抗能量攻击的目的。
1 时间随机化抗DPA攻击原理分析
设密码设备正常工作时的功耗采样信号为T[i][j],其中i为采样样本,j为采样点,由DPA攻击的原理可知,需要样本空间N足够大,即需要采集N组功耗数据。定义一组区分函数D[i][j]→(0,1),将采集到的功耗数据分为两组T0={T[i][j]|D[i][j]=0},T1={T[i][j]|D[i][j]=1}。当N足够大时,集合T0、T1中的样本数量近似相等,设为m,则采样点j处的差分功耗为:

差分功耗的数学期望为:
E(TD[j])=E(T[i][j]|D[i][j]=0)-E(T[i][j]|D[i][j]=1)
设在运算过程中插入随机延迟t后的功耗采样信号为T*[i][j],攻击者不知道插入随机时间延迟的情况下,仍然使用攻击正常工作设备时构造的区分函数D[i][j]来对数据进行分组处理,得到T={T*[i][j]|D[i][j]=0},T={T*[i][j]|D[i][j]=1},则采样点j处的差分功耗为:

此时,差分功耗的数学期望为:
E(T[j])=E(T*[i][j]|D[i][j]=0)-E(T*[i][j]|D[i][j]=1)
设随机延迟t有w种可能值,延迟t等于k的概率为pk,则插入时间延迟后的采样信号可表示为:
T*[i][j]=T[i][j-k]
那么,插入随机时间延迟后的差分功耗的数学期望可以表示为:

由DPA攻击的原理知,正常情况下,当密钥猜测正确时,差分功耗曲线会在时间点n处出现尖峰,设尖峰的幅值为A,其他点处与区分函数D不相关,所以差分功耗值约等于0,即:
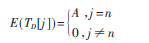
当插入随机延迟?驻t后,密钥猜测正确时的功耗曲线尖峰会分布在w+1个位置处,每个位置的差分功耗值为pk A,即:

以时间延迟t服从均匀分布为例,即pk=1/(w+1),则加入随机延迟后的差分功耗尖峰会均匀分布在w+1个位置上,且每个尖峰的幅值为A/(w+1)。
2 ECC处理器的时间随机化设计
为了更好地在ECC处理器中实现时间随机化,达到抗能量攻击的目的,必须分析时间随机化的设计要求和ECC处理器的特征,提出合适的设计方案。
2.1 ECC处理器时间随机化设计方案
结合上一节的分析,为了兼顾安全和效率两个方面,时间随机化设计需要满足以下要求:
(1)安全性好。功耗曲线上时间延迟部分不易被区分剔除,即要求时间延迟部分的功耗特性和算法中的正常运算操作的功耗特性相似,并且每次的延时时间随机产生。
(2)灵活性高。在正常计算过程中插入的延迟时间越长,抗能量攻击效果越好,但是对算法的效率影响也越大。因此,处理器的时间随机化设计需要满足不同的安全需求,能够根据具体情况选择一个安全与效率的平衡点,设置随机时间延迟的范围。
(3)方便使用。ECC处理器上的时间随机化设计,必须方便用户使用,用户可以根据需要在任意时刻执行时间随机化程序。
综合上述安全性、灵活性与易用性要求,本文借鉴软中断[8]的思想,对密码处理器进行时间随机化设计。在ECC处理器指令RAM中,存入一段不影响密码算法正常运算的冗余指令,利用中断指令来执行中断程序,随机地调用冗余指令,当中断结束后,正常程序的执行时间发生偏移,达到时间随机化的目的。由于时间随机化处理过程中执行的是冗余指令,所以其功耗特征与正常运算的功耗特征相似,单条能量迹中不易被区分。
2.2 基于软中断的时间随机化设计
时间随机化设计的一个关键因素是延迟时间的随机可控,既关系到抗能量攻击的效果,又关系到对密码运算的性能影响。为了设计灵活的控制单元,首先分析椭圆曲线密码处理器的特征:
(1)主要运算模块较少,椭圆曲线各层次的运算最终都是基于有限域层的运算实现的,域运算种类比较单一,主要包括为模乘、模逆、模加、模减等运算;
(2)运算指令周期较长,且同一运算指令处理不同长度数据时所用周期不同。表1给出了不同长度曲线对应的基本运算单元的时钟周期数。

椭圆曲线密码处理器的这些特征为时间随机化控制带来难度,不适合以指令条数为基本单位进行时间随机化控制。一方面,运算指令周期较长,以指令条数为粒度进行控制会对整个算法的性能影响较大;另一方面,不同的运算指令的周期不同,且处理不同长度曲线时,同一运算指令需要的时钟周期不一致,这样无法精确地控制插入的延时时间。考虑到用于实现随机化的冗余指令对于密码运算没有实际的意义,为了灵活控制随机化的程度,设计了以时钟周期为基本粒度的随机延迟控制单元,如图1所示。在执行中断程序时,生成一个随机数作为延时控制计数器的计数周期,当计数器计数结束后,产生一个进位信号CO。利用CO信号控制中断的返回,一方面参与生成运算模块的结束信号Valid,结束正在执行的冗余运算;另一方面用于生成堆栈寄存器的使能信号PP_EN和程序计数器PC的地址选择信号SEL,控制返回断点执行正常程序。随机数的值就是执行中断的时间,即时间随机化的延迟时间。

采用软中断的时间随机化设计,能够保证中断时间延迟部分的功耗特性与正常运算的功耗特性一致,在单条能量迹上无法将其区分出来。但是DPA攻击是通过分析大量能量迹来实施的,当随机化的首地址相同时,通过对比多条能量迹,仍然能够将延迟时间短的随机化部分区分出来,如图2所示。

为了解决这个问题,将冗余指令RAM的首地址加上可控的随机偏移地址作为中断的跳转地址,如图3所示,这样执行中断的部分就很难在能量迹中被区分剔除。
上述的延迟时间随机化设计解决了中断时间灵活控制的问题,跳转地址随机化设计解决了随机化功耗与正常运算功耗一致性的问题。本文设计了级数可变的伪随机数发生器,通过实际需求配置其级数来控制随机延迟和随机偏移地址的范围。在此基础上设计了带软中断的椭圆曲线密码处理器控制结构,并设计了软中断指令,支持时间随机化抗能量攻击功能,如图4所示。

3 时间随机化抗能量攻击能力验证
由于抗DPA攻击的时间随机化设计要求每次运算都要发生随机时间延迟,并且时间延时部分对应的功耗不能在单条能量迹上被区分,因此从三方面对设计进行验证:
(1)仿真验证运算操作的执行时间是否发生随机延迟;
(2)采集处理器执行密码运算的功耗曲线,观察时间随机化部分的功耗特性与正常运算时的功耗特性是否一致;
(3)进行DPA攻击仿真实验,验证其抗DPA攻击效果。
3.1 随机延迟仿真验证
以Montgomery点乘算法[9]为例,在处理器执行算法的过程中通过指令开启中断程序,任意两次相同输入的仿真中间结果如图5所示。

由图5可以看出,执行中断程序时,程序计数器PC(Current_PC)的值转向冗余程序地址,每次跳转地址不同,达到了跳转地址随机的设计要求,每次中断返回时间不同,达到了时间随机化的设计要求。
3.2 单条能量迹功耗特性一致性验证
采集处理器在执行加入软中断的算法时的功耗信息,如图6所示。

可以看出冗余运算部分与正常运算程序的功耗特性一致,不容易被区分剔除,满足了时间随机化部分不可区分的设计要求。
3.3 DPA攻击仿真验证
为了验证基于软中断的时间随机化设计的抗能量攻击能力,以Montgomery点乘算法为例,在执行时启动软中断程序,分别配置随机延迟范围为0~32个时钟周期和0~64个时钟周期,对其分别进行DPA攻击实验,并与正常运算的DPA攻击实验对比,结果如图7所示。
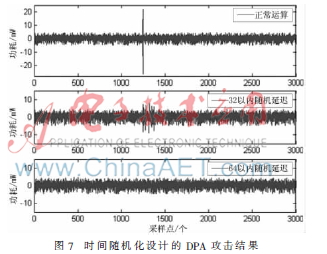
由图7可知,正常运算的差分功耗曲线上攻击点位置出现了明显的功耗尖峰,当加入32以内的随机时钟延迟时,尖峰值分布在多个位置上,幅值明显降低,理论上幅值是峰值的1/32,由于运算多为多周期,同一数据保持较长时间,加上噪声等影响,导致实际效果与理论分析效果有部分差异;当加入64以内的延迟时,差分功耗曲线上没有明显的尖峰值出现,达到了时间随机化抗DPA攻击的要求。
4 结束语
本文分析了时间随机化抗DPA攻击的原理,结合ECC处理器的处理特征,设计了基于软中断的时间随机化电路。搭建了功耗仿真平台,验证了本设计的抗DPA攻击能力。在处理器系统级进行设计,与具体的算法无关,具有较强的通用性,满足处理器的抗DPA攻击需求。
参考文献
[1] Victor Miller.Use of elliptic curves in cryptography[A].In:H.C.Williams.Advances in Cryptography-CRYPTO′85[C].Heidelberg:Springer-Verlag,1986:417-426.
[2] 倪乐.面向椭圆曲线密码的正规基模乘单元研究与设计[D].郑州:信息工程大学,2013.
[3] Stefan Mangard,Elisabeth Oswald,Thomas Popp.能量分析攻击[M].北京:科学出版社,2010.
[4] 段二朋,严迎建,李佩之.针对AES密码算法FPGA实现的CEMA攻击[J].计算机工程与设计,2012,33(8):2926-2930.
[5] BUCEK J,NOVOTNY M.Differential power analysis under constrained budget:low cost education of hackers[C].DigitalSystem Design(DSD),2013 Euromicro Conference on.IEEE,2013:645-648.
[6] 乐大珩.抗能量攻击的密码芯片电路级防护关键技术研究[D].长沙:国防科学技术大学,2011.
[7] 韩军.信息安全芯片的防御攻击技术研究[D].上海:复旦大学,2006.
[8] 马忠梅,马广云,徐英慧,等.ARM嵌入式处理器结构与应用基础[M].北京:北京航空航天大学出版社,2002.
[9] Darrel Hankerson,Alfred Menezes,Scott Vanstone.椭圆曲线密码学导论[M].北京:电子工业出版社,2005.

