0 引言

    LLC谐振功率变换器能够实现宽工作范围内的零电压切换，且在输入电压和负载大范围变化时开关频率变化范围较小，是一种当前备受关注的功率变换器。变频调制是谐振变换器常用的调制方法，但其频率变化范围较宽，不利于磁性元件的优化设计。

    自激移相调制（Self-Sustained Phase Shift Modulate，SSPSM）是由加拿大学者Mohamed Youseff提出的一种新的控制方法，该方法开关频率变化范围小，软开关特性好，输出调节能力强^[1]。文献[2-6]研究了基于自激移相控制的全桥LCC变换器的基本原理和设计方法。将自激移相控制应用于LLC谐振变换器还具有较大的研究空间。

    本文将系统研究基于自激移相调制的全桥LLC变换器的工作特性。

1 全桥LLC变换器的工作原理

    图1所示为全桥LLC变换器主电路，由开关网络、谐振网络、整流网络等组成，调制器采用自激移相调制。

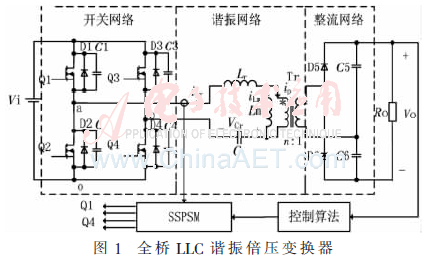
    图2所示为自激移相调制的波形图。该调制方法采用了两个控制变量γ_a和γ_b，γ_a为反向谐振电感电流-i_Lr与开关管Q₂漏源电压V_ao的相位差，γ_b为谐振电感电流i_Lr与开关管Q₄漏源电压V_bo的相位差，相位角γ_a和γ_b的差值对应全桥开关电路输出电压V_ab的零电平相位角。自适应锯齿波V_st为调制波，其归零时刻与谐振电流-i_Lr的过零时刻相一致，V_st的幅值应保持恒定。V_ca和V_cb为两路调制线，调制线与调制波相比较，并经逻辑电路转换，产生开关管的驱动信号。

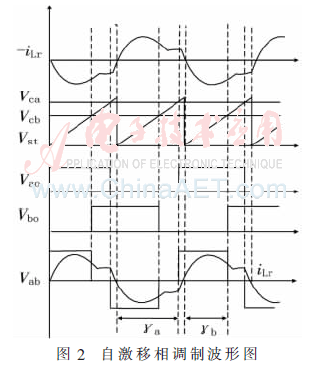
    自激移相调制有两根调制线，通常需要保持上调制线恒定以作为参考基准，而下调制线动态变化。下调制线由变换器的输出电压等状态量经PI等控制算法解算得到，下调制线和锯齿波相交时刻对应V_bo的上升和下降沿，则V_ab的脉宽主要受下调制线和自适应锯齿波的控制。

    若保证V_ca小于三角波的幅值，即γ_a<180°，则能实现谐振电流i_Lr始终滞后于V_ab。该调制方式通过可控的角度γ_a来实现开关管的驱动信号超前于谐振电流，进而保证开关管ZVS零电压开通。

2 LLC谐振变换器的建模

    采用基波分析法展开基于自激移相调制的LLC变换器的建模分析。基波分析法的思想是将变换器非线性环节的电压、电流量用其基波成分近似替换，从而达到使变换器线性化的目的。

    根据LLC谐振变换器中各元件的功能的不同，可以将其划分为开关网络、谐振网络和整流滤波网络三部分。

2.1 开关网络

    输入电压为V_in，开关网络为一个全桥逆变器，桥臂中点输出电压(a、b两点间电压)v_ab(t)为一个方波。设定i_Lr(t)=I_Lr·sinωt为基准，由图2中v_ab(t)和i_Lr(t)关系，可知：

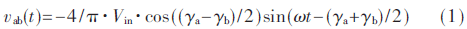
    则其有效值为：

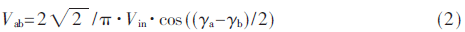
    故可将开关网络近似等效为一个有效值为V_ab的正弦输入电压源。

2.2 整流滤波网络

    设变压器副边电流为i_s。由于电流i_s经过整流后的平均电流和负载电流I_o相等，则：

    v_s与i_s同相位，因此整流网络可等效为一个纯阻性负载R_eq。可以推导出R_eq的表达式为：

2.3 变换器的等效电路模型

    经过以上简化处理后，可以得到全桥 LLC谐振变换器的近似等效电路，如图3所示。其中，R_ac=n²R_eq，为Req折算至变压器原边后的等效电阻。

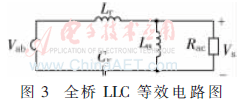
    根据基波等效电路，可得其传递函数：

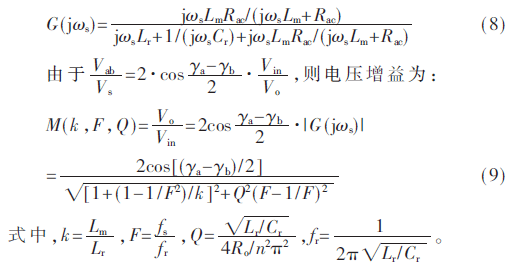
2.4 变换器的增益特性分析

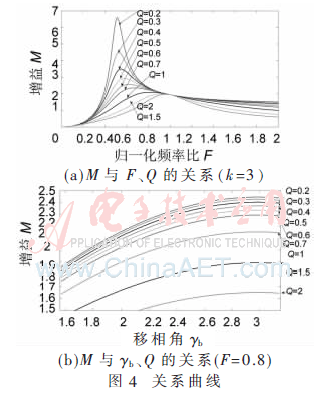
    根据得出的电压增益表达式，通过MATLAB绘出相关图形。图4(a)为增益随F和Q值变化的曲线图，可见F=1时电压增益几乎独立于负载，当开关频率偏离谐振频率时，增益随着Q值的增大而减小。

    图4(b)为增益随γ_b和Q变化曲线图，可见增益曲线随着γ_b的增大而增大，随着Q值的增大而减小。

3 自激移相调制下系统自振特性分析

    图5给出谐振变换器的简化结构，由线性部分G(S)和非线性部分N(X)串联。自振分析时r(t)=0。定义逆变输出的一次谐波分量和反馈谐振电流信号的复数比为非线性环节的描述函数N(X)。谐振网络的开关传递函数为G(S)。

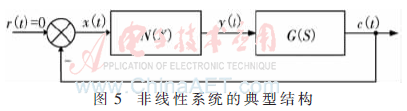
    非线性系统具有等幅振荡的条件是等效的开环幅频特性等于-1，即：N(X)·G(jω)=-1^[7]。在同一复平面内作出自变量从0变化到∞时G(jω)和-1/N(X)的曲线，有：若G(jω)曲线不包围-1/N(X)，则非线性系统稳定；若G(jω)=-1/N(X)，则系统可能出现自激振荡。但是并非所有交点都能构成稳定自激振荡，只有-1/N(X)轨迹的进行方向是由G(jω)的包围区过渡到非包围区的交点才能构成稳定自激振荡。

    由式(1)得非线性环节的描述函数为：

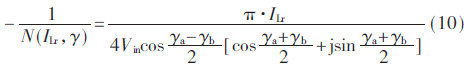
    取谐振电流为定值，在同一复平面上作出传递函数G(jω)和描述函数-1/N(X)的曲线，如图6(a)所示。可知，当γ_a、γ_b∈[0，π/2]时，曲线无交点；当γ_a、γ_b∈[π/2，π]时，曲线有交点，因此系统在该范围内存在自振点。为了确定这些自振点是否稳定，作出γ_a=γ_b=3π/4时传递函数G(jω)和描述函数-1/N(X)的曲线，如图6(b)所示。

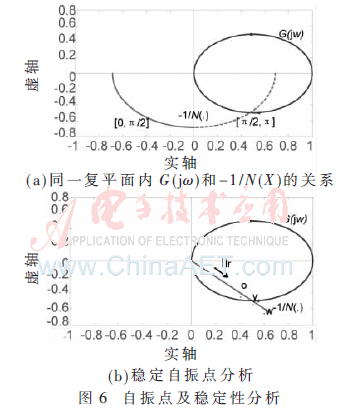
    随着谐振电流的增大，-1/N(X)的轨迹从G(jω)的包围区过渡到非包围区。

    当谐振电流变化导致y点移到G(jω)包围区的w点时，系统状态不稳定，振荡变大，并向y点移动并最终处于稳定状态。当y点移动到G(jω)非包围区的o点时，系统处于稳定状态，自振振幅减小，直至衰减为零，使系统重新回到y点处的状态。综上分析，该系统在γ_a、γ_b∈[π/2，π]时存在稳定的自振点。

4 实验研究

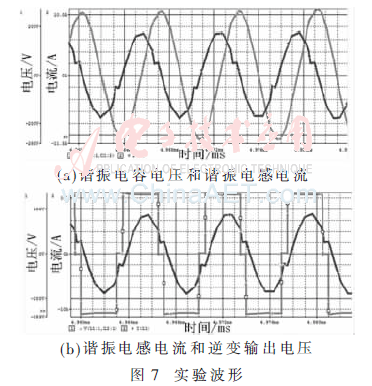
    根据前文理论，设计符合以下要求的变换器：输入电压V_in=270 V，输出电压V_out=1 200 V，功率P=800 W，开关频率f_s=140 kHz。取F=1.1，k=3，Q=0.2，r_a=5π/6，γ_b∈[π/2，5π/6]。根据本文分析进行实验，谐振参数：L_m=111.93 μH，L_r=37.31 μH，C_r=28.05 μH。图7(a)为谐振电容电压（峰值较大者）和谐振电感电流的波形图，可见两者均进行等幅的周期振荡；图7(b)为逆变输出电压（方波）和谐振电感电流的波形图，可以看出谐振电流滞后于谐振电压，变换器实现软开关特性。

5 结论

    自激移相调制全桥LLC变换器可大幅降低开关损耗，有效提高工作效率。本文对基于自激移相调制的全桥LLC工作原理进行了详细分析，并利用基波分析法对其进行数学建模，推导分析其电压增益特性；将非线性理论中的描述函数法应用到自激移相调制LLC变换器上，深入分析系统的自振特性；最后通过仿真验证了该调制方式的有效性。

参考文献

[1] YOUSSEF M Z，JAIN P K.Design of a front end series parallel resonant converter with self-sustained phase shift modulation controller[J].IEEE Transactions on Power Electronics，2004，19(2)：328-333.

[2] 廖鸿飞.自持振荡移相控制的全桥LCC谐振变换器的研究[D].广州：华南理工大学，2007.

[3] PAHLEVANINEZHAD M，EREN S.Self-sustained oscillating control technique for current-driven full-bridge DC/DC converter[J].IEEE Transactions on Power Electronics，2013，28(11)：5293-5310.

[4] YOUSSEF M Z，JAIN P K.A review and performance evaluation of control techniques in resonant converters[C].The 30th Annual Conference of the IEEE Industrial Electronics Society，Busan：IEEE Conference Publications，2004：215-221.

[5] YOUSSEF M Z，PINHEIRO H，JAIN P K.Self-sustained phase shift modulated resonant converters：modeling，design，and performance[J].IEEE Transactions on Power Electronics，2006，21(2)：401-414.

[6] YOUSSEF M Z.Control and modeling of high frequency resonant DC/DC converters for powering the next generation microprocessors[D].Queen′s University from Canada，2005.

[7] 吴俊娟，孙孝峰，邬伟扬.基于描述函数法的谐振变换器自持振荡研究[J].电力电子技术，2011，45(2)：53-55.