文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.10.041
中文引用格式: 张艳萍,姚俊,孙心宇. 一种基于相干波束形成的零陷加宽算法[J].电子技术应用,2015,41(10):150-153.
英文引用格式: Zhang Yanping,Yao Jun,Sun Xinyu. A novel null broadening algorithm based on coherent interference beamforming[J].Application of Electronic Technique,2015,41(10):150-153.
0 引言
波束形成是阵列信号处理中的一个重要研究方向,被广泛应用于通信、雷达信号处理中[1]。自适应波束形成器能够自动将主波束对准期望信号方向,将零陷对准干扰方向,从而很大程度地提高系统的输出信噪比。然而在实际情况中,不可避免的有智能干扰、多径反射等因素的存在,造成期望信号和干扰信号相干,使传统系统无法有效消除相干的干扰信号。同时由于干扰扰动或者天线接收平台发生振动的情况,导致干扰信号移出零陷位置从而不能被有效地消除[2]。这些都将使系统输出信干噪比严重下降。
针对干扰信号与期望信号相关的问题。肖红侠等[3]提出了一种基于多约束最小均方算法的空域调零技术来抑制相干干扰,Zheng Guimei等[4]提出了一种加权极化平滑算法,但计算量较大。刘张林[5]提出了一种基于空间平滑的算法来去相干。
针对干扰信号发生扰动的问题。MAILLOUX R J[6]和ZATMAN M[7]提出了不同的零陷加宽方法,但两种方法本质上是相同的。GERSHMAN A B[8]提出了一种在干扰方向施加导数约束从而加宽干扰零陷的方法,但该方法运算量较大。王妙等[9]提出了一种基于降秩共轭梯度法的零陷加宽算法。
本文提出了一种基于前后空间平滑的零陷加宽算法。该算法先利用前后向空间平滑的方法有效去除了相干性,并利用迭代求得最优权矢量。再将迭代求得的最优权矢量作为一个“标准”的输出权值,利用二次约束的方法使方向图零陷得到展宽。最后通过计算机仿真,对算法的性能进行验证。
1 算法描述
1.1 阵列结构与信号模型

图1为M元均匀直线阵列,阵元间距为d(d=?姿/2)。假设有K个远场窄带信号入射到阵列上((M+1)/2>K),其中包括一个期望信号s0(t)和K-1个未知的干扰信号(其中有n个与期望信号相干)sl(t)(l=1,…,K-1),则第i个阵元在t时刻所接收的数据信号模型可以表示为:
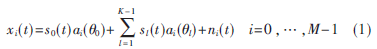
式中:表示第i个阵元对第l个信号的空间响应,ni(t)为第i个阵元上的高斯白噪声。
阵列的接收信号可表示为:
X(t)=AS(t)+N(t)(2)
式中:X(t)为阵列的M×1维快拍数据矢量,S(t)为信号的K×1维矢量,N(t)为阵列的M×1维噪声数据矢量,A为空间阵列的M×K维流型矩阵。
当信号源相干时,相干信号源间只差一个复常数,假设有n(n<K-1)个干扰与期望信号相干,第i个相干干扰可以写为:

将式(3)代入式(2),得相干信号源模型:
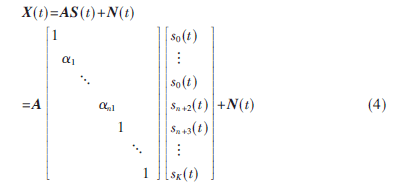
1.2 前后向空间平滑波束形成算法
当期望信号和干扰信号相干时,导致系统不能在所对应的干扰方向形成零陷,干扰不能被有效消除,严重影响输出信干噪比。
本文利用前后向空间平滑技术对期望信号和干扰信号进行解相干处理。将均匀线阵(M个阵元)分成相互交错的P个子阵,每个子阵所含的阵元数为m=M-P+1,取最左边的子阵作为参考子阵,如图2所示。

则第k个子阵有如下数据模型:
Xk(t)=[xk(t) xk+1(t) … xk+m-1(t)]=Am D(k-1)S(t)+Nk(t)(5)
式中:Am为子阵的阵列流行,D为每个入射信号在相邻阵元引起的固定相位差对角矩阵,Nk(t)为第k个子阵上的高斯白噪声。
则第k个子阵所接收数据的协方差矩阵为:

式中:H为共轭转置,Rs为协方差矩阵。
则前向空间平滑的协方差矩阵为:
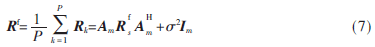
再取最右边的子阵作为参考子阵,同理,则后向空间平滑的协方差矩阵为:

由于Rb就是Rf的共轭倒序阵,它们之间满足共轭倒序不变性。因此整个均匀线阵前后空间平滑后的数据协方差矩阵为:

再利用抽样矩阵梯度算法(Sampling Matrix Gradient,SMG)[10]迭代的方法求取最优权矢量,由约束最小功率准则[11]:

在此约束条件下,使得wHRw最小。式(10)中:w为算法的权矢量,R为入射信号数据协方差矩阵,ad是期望信号导向矢量。
由梯度算法得:

从以上分析可以看出,最陡下降法不需要积累足够多的快拍数据后再进行权矢量计算,迭代求得最优权值 wSMG。常规的线性约束最小方差算法[11]在求最优权矢量时,计算量为O(M3)。本文采用最陡下降的递推方法,去除了矩阵求逆,由式(14)可知,计算量为O(M2),运算量降低了一个数量级,有效减少算法运算量。
1.3 零陷加宽
当干扰源快速移动等情况下,都可能使干扰移出方向图的零陷位置,导致干扰的“欠相消”。本文将迭代求得的最优权矢量wSMG作为一个“标准”的波束形成器的输出权值,再利用二次约束的方法,得到具有展宽零陷的最优权矢量wopt。

因此本文算法具体步骤如下:
(1)利用前后空间平滑方法得到去相干后的数据协方差矩阵:

(2)利用SMG迭代求取最优权矢量:

(3)将步骤(2)中迭代求得的最优权矢量wSMG作为一个“标准”的波束形成器的输出权值,再利用二次约束的方法,得到具有展宽零陷的最优权矢量:

2 性能仿真
为了验证本文方法的正确性和有效性,在计算机上进行仿真实验。仿真采用15个各向同性的阵元组成的均匀直线阵,子阵列的个数为10,每个子阵列的阵元数为6,快拍数为1 000,蒙特卡罗实验次数为200次。期望信号的方向为0°,两个干扰信号的方向分别为-40°(与期望信号相干)和30°,入射信噪比和干噪比分别为SNR=0 dB,INR=30 dB。仿真结果如图3~图5。
(1)实验一:方向图对比仿真
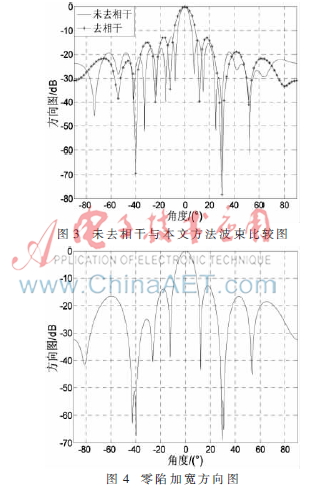
从图3可以看出,未去相干的波束形成算法只能在非相干干扰方向(30°)形成零陷,而本文的波束形成算法在相干干扰(-40°)和非相干干扰(30°)方向均形成了较深的零陷,较好地抑制了相干干扰。
(2)实验二:方向图零陷加宽仿真
其他仿真条件不变,零陷深度系数?着=10-7,仿真结果如图4所示。
从图4可以看出,在干扰信号方向-40°和30°处均形成了的零陷。当干扰信号发生扰动时,依然处在零陷范围内,使得干扰信号能够较好地被消除。
(3)实验三:输出SINR与输入SINR仿真
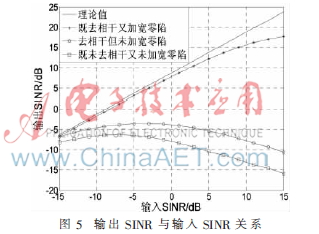
其他仿真条件不变,输入信干噪比由-15 dB变化到15 dB,仿真结果如图5所示。
从图5可以看出,在相干的干扰信号发生扰动的情况下。既未去相干又未加宽零陷的波束形成算法的输出SINR损失严重。去相干但未加宽零陷的波束形成算法由于干扰信号偏离出了零陷位置,造成输出SINR下降。而既去相干又加宽零陷的波束形成算法由于相干干扰信号较好的被消除,因此对输入SINR的变化并不敏感,在输入SINR整个变化过程中,输出SINR损失最大约为5 dB。从而进一步验证了本文方法的有效性。
3 结论
实际环境中不可避免的存在着相干干扰信号和干扰扰动的情况。本文研究了一种在相干信号环境下零陷加宽的方法。通过实验仿真发现,该方法有效地去除了干扰信号与期望信号之间的相干性。当干扰发生扰动时,仍然能使系统具有较好的输出SINR。因此本文方法是一种较好的稳健相干波束形成算法。
参考文献
[1] 张小飞,汪飞,陈华伟.阵列信号处理的理论与应用[M].北京:国防工业出版社,2013.
[2] ZATMAN M.Comments on theory and application of cova-riance matrix tapers for robust adaptive beamforming[J].IEEE Transactions on Signal Processing,2000,48(6):1796-1800.
[3] 肖红侠,项建弘.基于调零技术的相干干扰抑制方法[J].计算机应用研究,2013,30(6):1779-1782.
[4] Zheng Guimei,Chen Baixiao,Yang Minglei,et al.Weighted polarization smoothing algorithm for electromagnetic vector-sensor array[J].Systems Engineering and Electronics,2012,34(4):637-643.
[5] 刘张林.相干信号源自适应波束形成[J].雷达与对抗,
2011,31(3):23-30.
[6] MAILLOUX R J.Covariance matrix augmentation to producearray pattern troughs[J].Electronics Letters,1995,31(10):771-772.
[7] ZATMAN M.Production of adaptive array troughs by disper-sion synthesis[J].Electronics Letters,1995,31(25):2141-2142.
[8] GERSHMAN A B,NICKEL U,B?魻HME J F.Adaptive beamforming algorithms with robustness against jammer motion[J].Signal Processing,IEEE Transactions on,1997,45(7):1878-1885.
[9] 王妙,方明.一种秩基于降秩共轭梯度法的零陷加宽技术[J].电子信息对抗技术,2011,31(4):1674-2230.
[10] BERTRAND A,MOONEN M,SAYED A H.Diffusion bias-compensated RLS estimation over adaptive networks[J].IEEE Trans. on Signal Processing,2011,59(11):5212-5224.
[11] FROST O L.An algorithm for linearly constrained adaptive
processing[J].Proc.IEEE,1972,60(8):926-935.

