文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.10.044
中文引用格式: 周先春,唐娟,汪美玲,等. 曲率与小波轮廓增强的人脸识别算法[J].电子技术应用,2015,41(10):161-164.
英文引用格式: Zhou Xianchun,Tang Juan,Wang Meiling,et al. Face recognition algorithm based on curvature and wavelet contour enhanced[J].Application of Electronic Technique,2015,41(10):161-164.
0 引言
人脸识别具有广泛的应用价值,主要包括:主成分分析法[1]、线性判别分析法[2]、独立主元分析[3]和支持向量机(SVM)[4]方法等。然而,当光照、表情和遮挡不同时,这些方法的识别率和鲁棒性会大大降低。为了提高识别方法的鲁棒性,Wright等将稀疏表示(Sparse Representation-based Classifier,SRC)推广应用到人脸识别中,提出了稀疏表示的人脸识别算法及一些扩展算法[5]。2012年DENG W H等[6]提出了扩展SRC算法,提高了识别性能;Xu Yong等[7]提出了二重测试样本稀疏表示方法;Lai Jian等[8]提出了模块加权的稀疏表示人脸识别等。虽然基于稀疏表示的人脸识别算法得到了广泛应用[9],但该算法是通过求解l1范数最小值问题来进行识别,由于实际应用中每个人的人脸数据有限,会存在“维数灾难”的问题,因此Min Rui等[10]对此作出了改进,但该算法在非约束条件下,鲁棒性降低。
本文利用了水平集曲率及SRC的优点,提出了一种曲率与小波轮廓增强的人脸识别算法,该算法充分利用了水平集曲率的性质、人脸图像轮廓的不变性和人脸图像轮廓对光照的不敏感性,在稀疏表示现有的理论基础上,提高了非约束性人脸的识别率,增强了识别系统的鲁棒性。
1 基于曲率与小波的人脸特征提取
1.1 水平集曲率
由于曲率?资是切矢量T(s)的旋转角速度,同时也是法矢量N(s)的旋转角速度,则:

I与水平集的切矢量相垂直,即与水平集的法矢量平行。另一方面,根据式(5),梯度矢量总是指向I值增大的方向,所以水平集的单位法矢量可表示为:

一般约定式(6)取负号,把式(6)代入式(3)中,便可求得函数I(x,y)水平集曲率为
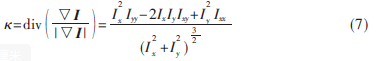
1.2 特征提取
本文算法过程如下:
(1)检测:将水平集曲率作为一个检测因子,检测图像的轮廓。为检测图像的整体结构,建立结构控制函数:

其中,f是以图像I的曲率为自变量的结构函数,它的作用在于检测图像整体结构,如图1所示。为得到图像的整体轮廓,进一步建立融合轮廓分布模型:

式中,轮廓分布图像,I是原始图像,可通过拟合得到稀疏系数,式(9)可得到原图像与轮廓相融合的图像,如图2所示。

(2)增强:用小波对图像进行分解,本文设定图像的高频系数为350,若大于该高频系数,则使高频系数增大为原来的2倍,否则缩小为原来的一半,以此来突出图像的轮廓与整体结构,弱化细节,如图3所示。

图3表明,处理后的增强图像的直方图的峰值出现在直方图的较右部分,图像较亮,可有效地增强人脸的整体轮廓,从而避免了人脸识别中光照、人脸表情和一些遮挡物的影响。
(3)提取:用PCA方法提取轮廓增强图的特征,如图4所示。

2 稀疏表示的分类识别
对训练样本与测试样本用上述方法做特征提取后,归一化处理,得到训练样本,可表示为:
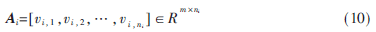
故同一类别的测试样本向量被训练样本线性组合为:
y=ai,1 vi,1+ai,2 vi,2+…+ai,j vi,j(11)
式中,ai,j∈R,j=1,2,…,ni,ai,j表示样本的系数。
在实际中,由于测试样本的类别是未知的,因此可将训练样本组合在一起形成一个训练集矩阵A:

求解C,得到该矩阵的特征向量,选取该矩阵的最大特征值对应的特征向量,得到特征子空间Z,计算训练样本在Z中的投影向量,将投影后的向量生成冗余字典。
在降维之后,为了计算稀疏表示系数x,需要求解最小l0范数问题,但该范数是一个Np-hard问题,难以直接求解。Donoho等人指出,可通过求解如下的凸优化问题,正确恢复稀疏矢量x:

式中,为所求稀疏表示系数,用于分类识别。
下面给出本文算法的流程图,如图5所示。

3 实验结果与分析
本文所用的数据集来自著名的ORL人脸库,ORL数据库共有400幅人脸图像(40人,每人10幅)。在实验过程中将人脸库中的图像分成两部分,每部分5张图像,一部分作为训练图像,一部分作为测试图像,实验结果如表1和图6所示。
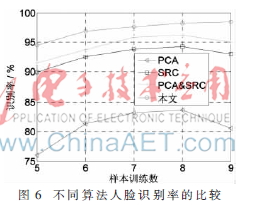
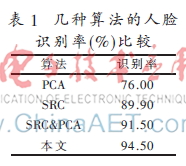
由表1可知,本文提出的算法与PCA算法、SRC算法、PCA&SRC算法相比,识别率最高提高了18.5%。观察图6,随着训练样本数的增加,本文算法的识别率能够稳定的增加,最高能够达到98.50%,而PCA算法、SRC算法、PCA&SRC算法的识别率随着训练样本的增加出现下降的趋势,故本文算法的识别系统鲁棒性较其他算法好。
4 结论
基于ORL人脸库的仿真结果表明,本文所提算法提高了人脸识别率,识别系统鲁棒性较其它算法好。本文算法综合了PCA和SRC算法的优点,并基于曲率和小波对图像轮廓进行了增强,将形态学特征应用到人脸识别中,丰富了人脸识别的内容的人脸识别算法。利用了轮廓不变性及轮廓对光照的不敏感性,以及小波增强图像的整体轮廓,增强了算法的鲁棒性。
参考文献
[1] 温浩,卢朝阳,高全学.融合小换波变和张量PCA的人脸识别算法[J].西安电子科技大学,2009,36(4):602-607.
[2] 余冰,金连甫,陈平.利用标准化LDA进行人脸识别[J].计算机辅助设计与图形学报,2003,15(3):302-306.
[3] 范群贞,刘金清.基于PCA/ICA的人脸特征提取新方法[J].电子测量技术,2010,33(8):31-34.
[4] TAN Y,WANG J.A support vector machine with a hybrid kernel and minimal Vapnik-Chervonenkis dimension[J].IEEE Transactions on Knowledge and Data Engineering,2004,16(4):385-395.
[5] WRIGHT J,MA Y,MAIRAL J,et al.Sparse representation computer vision and pattern recognition[J].Proceedings of the IEEE,2010,98(6):1031-1044.
[6] DENG W H,HU J,GUO J.Extended SRC:Undersampled face recognition via Intra-Class variant dictionary[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2012,34(9):1864-1870.
[7] Xu Yong,Zhang David,Yang Jian,et al.A two-phase test sample sparse representation method for use with face recognition[J].IEEE Transactions on Circuits and Systems for Video Technology,2011,21(9):1255-1262.
[8] Lai Jian,Jiang Xudong.Modular weighted global sparse representation for robust face recognition[J].IEEE Signal processing letters,2012,19(9):571-574.
[9] Yang Meng,Zhang Lei,Feng Xiangchu,et al.Fisher discri-mination dictionary learning for sparse representation[C].Proceedings of Computer Vision(ICCV),2011 IEEE International Conference on.Los Alamitos:IEEE Computer Society Press,2011:543-550.
[10] Min Rui,DUGELAY J L.Improved combination of LBP and sparse representation based classifycation(ARC) for face recognition[C].Proceedings of Multimedia and Expo(ICME),2011 IEEE International Conference on.Los Alamitos:IEEE Computer Society Press,2011:1-6.

