0 引言

　　随着通信业务的高速发展，无线电频谱的低端频率已趋于饱和，频谱资源匾乏的问题日益严重[1]。为了解决频谱利用率的问题，Joseph Mitola于1999年在软件无线电的基础上提出了认知无线电的概念[2]。要实现动态频谱接入，首先要解决的问题就是如何检测频谱空穴，也就是频谱感知技术。传统频谱感知的解决方案主要有数字和模拟两类，常见的模拟方式类似实验室的扫描机制，需要可调的线路和独立的认知无线电接收设备。数字的形式要求采样率满足奈奎斯特采样定理，当工作在宽带环境下，采样率可能会相当大。所以宽带信号频谱感知的难点主要在于现有硬件设备的模数转换和信号处理能力尚无法满足对宽带信号需求的高速增长。因此宽带信号频谱感知的研究将主要集中在如何利用宽带信号的稀疏特性通过较低的采样率获得宽带信号的部分信息进行频谱感知[3]。认知无线电的广泛应用要建立在创新的频谱感知技术上。

　　本文提出一种基于稀疏傅里叶变换（Sparse Fourier Transform，SFT）的频谱感知方法，尤其适用于宽带认知无线电。系统结构有两个优点，一是模拟前端是固定的，不涉及扫描硬件；二是模数转换器和数字信号处理采样率都低于奈奎斯特率。稀疏快速傅里叶变换的算法最早于2012年由MIT的研究人员提出[4]。利用稀疏傅里叶变换的算法，数据流的处理速度会比快速傅里叶变换还要快10～100倍，用在频谱感知这样海量大数据处理方面更能凸显其优势。

1 传统频谱感知模型

　　最初对于宽带信号检测的研究都集中在窄带频谱检测方面，每个节点在一个检测周期内只能检测一个窄带信道，在完成此次检测任务后才能进入下一个信道的检测。这样对于单个认知无线电用户来说，不但需要有精确的检测性能，而且需要很长的检测时间才能完成宽带范围内的频谱空闲检测。2008年11月的IEEE Signal Processing Magazine综述了现有的认知无线电技术[5]。根据文献[6]将当前的频谱感知方法总结在表1中。

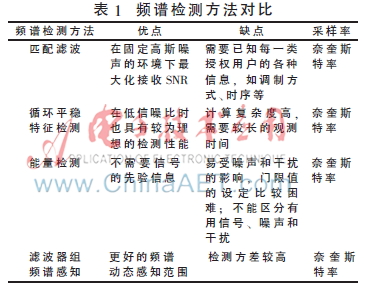
　　单节点的窄带频谱检测由于使用条件的不同，在不同的环境下检测性能会有比较大的变化。为了适应无线移动通信宽带化的发展趋势，又提出了多节点协同宽频带检测机制。每个节点由多条射频电路组成，需要多个带通滤波器，每条窄带链路采用简单的能量检测算法。但是节点的硬件电路一旦固定，各个滤波器的范围就随之固定。因此这种方法只适用于各个子频带预先知道并且固定的情况，即需要知道足够的先验信息，对于子信道分配的先验信息未知的情况则无能为力。

2 基于稀疏傅里叶变换的频谱感知模型

　　传统的方法需要的采样率过高，无法真正满足动态检测宽带频谱的要求。本文的频谱感知模型如图1所示。利用SFT的思想采用低于传统奈奎斯特采样率的方式直接对宽带信号进行低速采样，并重建原宽带信号频谱。

　　介绍采样算法之前，首先介绍一下傅里叶变换的基本特性：信号时域的二次抽样引起频域的混叠，图2证明了这种特性。对图2左上图时域的二次抽样产生了左下图。在频域，二次抽样后信号的快速傅里叶变换（Fast Fourier Transform，FFT）是原信号FFT的混叠，也就是说样点6和1叠加，7和2叠加，以此类推。稀疏傅里叶变换的算法主要分为混叠滤波、估计和冲突检测三步。下面重点解释这三步。

　　2.1 混叠滤波

　　为了降低采样率，以抽样因子p对时域进行二次抽样，通过时域的抽样达到频域混叠的效果。因为频域是稀疏的，所以混叠后只有少数频率分量上的值非零。x是长为N的离散时间信号，X是它的频域表示。x′是x抽样后的信号，其中x=xi×N/B，B可以整除N。那么X′就是抽样后的x′的FFT：

　　因此，混叠是抽样后进行FFT的一个结果，频率等间隔B被分配到同一个频率单元上，例如f将会分到桶i=f mod B。另外，每一个频率单元的值是所有映射到其中的频率值的总和。

    2.2 频率估计

　　如果混叠滤波后一个非零频率和多个零值频率映射到同一个频率单元，则认为不发生冲突，此时无法确定非零频率的具体位置f。为了计算f，利用FFT的相位旋转属性，即时域的移位会转换为频域的相位旋转。在输入信号移位个采样点后重复整个混叠的过程。由于时域的延时转换为频域的相位旋转。相位改变为：

　　因此，利用相位差即可求出非零频率的位置f，这个过程称为估计。对于所有不发生冲突的频率单元，估计出原频谱中非零频率的位置和频率值，也就是f和对应的Xf。

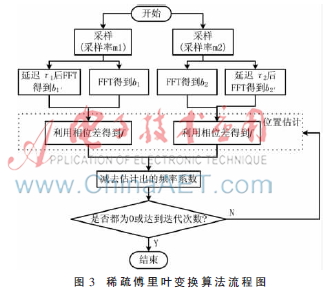
　　2.3 冲突解决和检测

　　如果混叠的过程中两个及以上的非零频率映射到同一个频率单元则称为冲突。同样利用FFT的相位旋转属性可以检测是否有冲突发生。如果不发生冲突，则一个频率单元中映射进来的频率仅仅有一个非零频率f，在两次延时不同的混叠过程中的频率单元的值通过比较延时前和延时后的幅值是否相同，可以判断是否发生冲突。

　　检测出冲突后，可以对互质采样的混叠滤波进行解决。证明只要采用互质的采样间隔随机化混叠时的频率位置，就可以防止同一个频率对在两次混叠中都发生冲突。然后在两次混叠过程间迭代就可以找到所有的非零频率。SFT的具体流程图如图3所示。

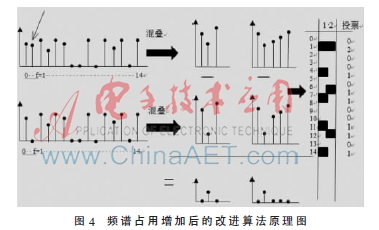
　　由于稀疏傅里叶变换要求应用在频谱占用率不超过10%的情况，当频谱占用率增加到大于10%后，不能再采用这种方法进行频谱的稀疏恢复。但是因为一段时间内一个地区的频谱占用情况不会经常发生变化，可以认为在当前观察的时间窗和下一时间窗内频谱的变化是稀疏的，利用这个频谱变化的稀疏性进行稀疏傅里叶变换。由于此时能量发生变化，不能再利用相位循环来找到变化的频率位置，考虑在两次混叠滤波后相减找到变化的频率混叠后的位置，然后采用投票的方式判断出最终状态发生变化的频率位置。将每次可能映射到其中的频率位置做个投票，如果某频率位置在两次混叠后都获得了投票，则认为此频率位置为恢复后的变化频率位置。算法原理图如图4所示。

3 算法性能仿真

　　为了验证稀疏傅里叶变换用于宽带频谱感知的性能，利用MATLAB平台进行仿真分析。首先频谱稀疏信号采用以下形式产生：

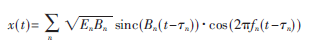
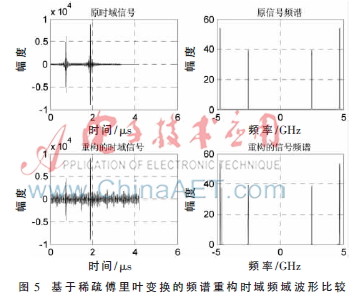
　　其中En、Bn、fn、n分别代表第n个频带的能量系数、带宽、载波频率和延迟时间。为了仿真实际采样过程，用2倍奈奎斯特率的离散信号来表示连续信号，利用抽取的方法实现滤波后的采样过程。采样5 GHz的信号至少需要10 GHz的采样率，而使用稀疏傅里叶变换需要的采样率为420 MHz和500 MHz(抽样因子为21和25，则可观测带宽为10.5 GHz)。图5给出了该算法重构前后信号的时域和频域形式。如图所示，时域和频域的重构结果均较好地再现了原信号的波形和频谱，说明在信号频谱相对稀疏的情况下，稀疏傅里叶变换可以较好地进行频谱检测。

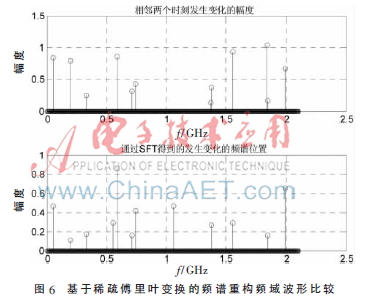
　　当频谱的占用增加到50%时，时间窗长度为10 s，假设状态发生变化的频率分量占总数的3%，利用改进算法成功恢复出状态发生变化的频率位置如图6所示。由于只关心频谱是否被占用，而不关心具体的频率幅度，所以认为改进的算法可以成功地找到变化的频率位置。

4 算法性能评估

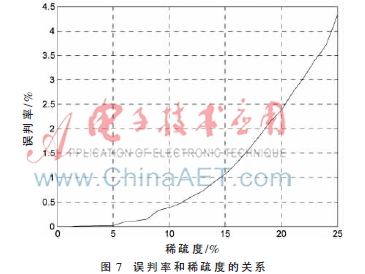
　　误判率：占有频率被SFT判断为空闲的百分比。对于不同稀疏性的情况下，仿真得到误判率和稀疏性的关系如图7所示。可以看出在稀疏度小于10%时，误判率不超过0.5%，当稀疏度高达25%时，误判率也不超过5%。

　　运算复杂度：FFT计算N点DFT时，其运算复杂度为O(N log2 N)。而SFT只需要4次混叠的过程，即其运算复杂度仅为O(2B1log2 B1)+O(2B2log2 B2)。假设B1>B2，则复杂度为O(B1log2 B1)。当N比较大时，SFT的效率提高更加明显。

　　采样率：直接对一个5 GHz信道进行宽带信号频谱检测需要10 GHz的采样率，而使用SFT可以使用500 MHz和420 MHz的采样率，采样率大约降低到原来的20%，硬件上易于实现，且效率更高。

5 结论

　　本文通过分析传统频谱感知方式的不足，提出了一种基于稀疏快速傅里叶变换的宽带频谱感知方法。该方法能够以若干低速ADC完成对宽带频谱信号的采样，解决了宽带频谱感知中采样速率过高的问题，为亚奈奎斯特采样的宽带频谱感知提供了一种新的思路。

参考文献

　　[1] Mishali Moshe，Eldar Yonina C.Wideband spectrum sensing at sub-nyquist rates[J].IEEE Signal Processing Magazine，2011，28(4)：102-135.

　　[2] 盖建新，付平，乔家庆，等.用于宽带频谱感知的全盲亚奈奎斯特采样方法[J].电子与信息学报，2012，34(2)：361-367.

　　[3] Ahmad B I，Al-Ani M，Tarczynski A，et al.Compressive and non-compressive reliable wideband spectrum sensing atsub-Nyquist rates[C].Signal Processing Conference(EUSIPCO)，2013 Proceedings of the 21st European IEEE，2013：1-5.

　　[4] HASSANIEH H，SHI L，ABARI O，et al.GHz-wide sensingand decoding using the sparse Fourier transform[C].，2014 Proceedings IEEE，2014：2256-2264.

　　[5] RAMOS S，FEIJO C，GMEZ-BARROSO J L.Next gen-eration mobile network deployment strategies[J].Journal of the Institute of Telecommunications Professionals，2009，3(1)：13-19.

　　[6] GOGGIN G.Adapting the mobile phone：the iPhone and its consumption[J].Continuum: Journal of Media & Cultural Studies，2009，23(2)：231-244.