0 引言

　　随着人们对无线频谱资源需求量的与日俱增，无线频谱资源已经成为一种稀缺性资源，由于当前的频谱固定分配机制，导致了频谱资源的严重浪费。认知无线电(Cognitive Radio，CR)[1]作为一种新兴的动态频谱接入技术，可以有效改变这一困境。次级用户(Secondary User，SU)为了能动态接入未经主用户(Primary User，PU)占用的授权频带(Licensed Frequency Bands，LFB)，需要SU准确地感知LFB是否被占用，因此，频谱感知技术无疑是CR中的一项核心技术。传统的频谱感知技术研究通常聚焦于窄带以及多用户协作[2]方面。近几年，宽带频谱感知(Wideband Spectrum Sensing，WSS)逐渐成为了CR技术研究中的热点研究方向。当前，主要的WSS研究都建立在需要知道PU信号和噪声功率等先验信息的基础上，在通常情况下缺乏灵活度和鲁棒性。因此，基于信号集合势(Signal Set Cardinality，SSC)的WSS算法由于无须预知PU先验信息，且可以避免对噪声功率的精确估计，成为了研究的重点[3-4]。基于SSC的WSS主要是利用信息论准则(Information Theory Criterion，ITC)[5-6]，估计LFB上被PU占用的子带个数并最终确定被PU占用的子带的位置。由于估计的效果不佳，导致了基于ITC的WSS方案的检测效果欠佳，尤其是在低信噪比的情况下。

　　为了克服上述研究的不足，提出了基于灵活检测准则(Flexible Detection Criterion，FDC)的宽带频谱感知算法。经理论推导和计算机仿真实验证明，基于FDC的WSS算法比基于ITC的WSS算法感知性能更好，并且，经Gerschgorin似然估计(Gerschgorin Likelihood Estimate，GLE)改进之后可进一步提高感知性能。此外，FDC感知算法还可以通过改变灵活系数的值以适应不同环境的要求，具有很强的实用性。

　　1 宽带感知系统模型

　　在宽带频谱感知系统模型中，SU接收机将整个LFB分成Q个子带且每个子带带宽均为WHz，如图1上半部分所示。其中，P个PU的工作状态是相互独立的，一共占用了K个子带。假设被PU占用的子带集合为SPU=Sp，空闲子带集合为S0，PU信号的相关信息均未知。在各个子带的频谱感知判决完成后，被PU占用的子带集合为PU，空闲子带集合为0，如图1下半部分所示。为了避免虚警和漏检测情况的发生，WSS的目的就是使PU与SPU尽量保持一致。

　　令Hq，1表示第q个子带处于被占用的状态，Hq，0表示其处于空闲状态。在接收端，第q个子带的第次快拍频域采样信号为rq：

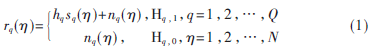
　　其中，hq表示第q个子带上的等效信道增益， sq表示第时刻第q个子带上对应的PU信号成分，nq(?浊)表示在第q个子带上接收到的加性高斯白噪声。N为感知时间内的快拍次数。在WSS中实现能量检测，一般可采用独立子带门限检测(Individual Subband Threshold Test，ISTT)。

　　在SU接收端，第次快拍时Q个子带的采样信号为r，。

　　由式(1)可得，空闲子带的功率只来源于噪声，被PU信号占用的子带的功率由信号和噪声共同组成。假设Q个子带中有K个被PU信号占用，计算出第q个子带的N次采样能量值为eq(q=1，2，…，Q)，将eq按照降序排列：

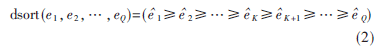
　　2 基于FDC准则的感知算法

　　2.1 基于GLE改进的信息论准则算法

　　基于SSC的宽带频谱感知技术主要利用ITC中的Akaike信息准则(Akaike Information Criterion，AIC)与最小描述长度(Minimum Description Length，MDL)准则来估计LFB上被PU信号占用的子带个数。AIC和 MDL的具体函数表达式[3]分别为：

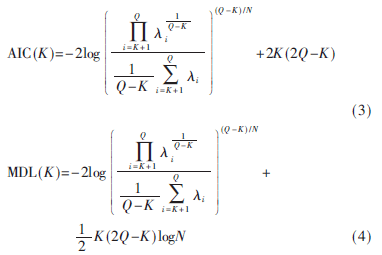
　　其中，假设LFB上被PU信号占用的子带个数为K，K∈{0，1，2，…，Q-1}，将采样信号协方差矩阵R的Q个特征值按从大到小的顺序排列，i表示采样信号协方差矩阵R的第i个特征值，式(3)和式(4)等式后的第一项为对数似然函数项，第二项为惩罚函数项。

　　可判断的是，对数似然函数项的取值越小，对应的K值在概率上越接近真实值。因此，可得：

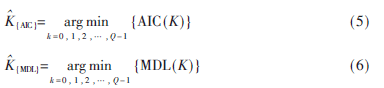
　　即当上式函数值取得最小值时，则得到PU占用子带集合势。

　　基于ITC算法的WSS性能不是很理想，这主要是因为ITC算法仅考虑采样信号协方差矩阵的特征值信息，从而导致在低信噪比的情况下算法检测性能不佳，因此，考虑将GLE算法引入ITC算法中。

　　Qing等[7]给出了基于GLE算法改进的GAIC和GMDL的函数表达式：

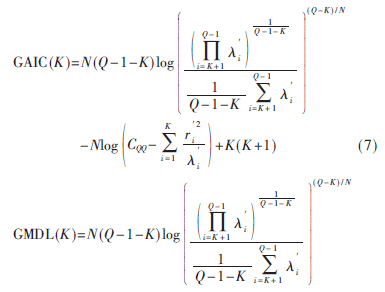
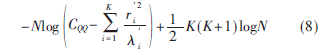
　　其中，CQQ为采样信号协方差矩阵R第Q行Q列的值，r分别为第i个Gerschgorin圆盘的半径和圆心[8]。式(7)和式(8)等式后的第一项为对数似然函数项，后两项为惩罚函数项。

　　类似地，在WSS方案中通过式(7)和式(8)得到GLE判决方程:

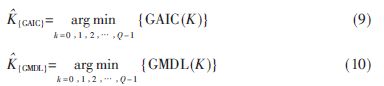
　　虽然GAIC和GMDL算法的感知性能稳定，但是仍然不能很好地满足更高的检测率和较低的虚警率的要求。从估计PU占用的子带个数的角度来说，GAIC和GMDL算法仍是低估了实际的PU占用的子带个数。因此，本文提出一种基于灵活检测准则的WSS算法，可有效地改善MDL、GMDL算法低估PU占用子带个数的情况。

　　2.2 基于FDC准则的宽带频谱感知算法

　　为了减小低估，FDC准则引入了灵活系数t，且t>1。保持惩罚函数项不变，替换对数似然函数项中的?姿为?姿t，FDC-MDL[9]方程表达式为：

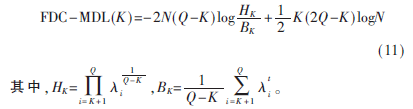
　　运用FDC准则的条件是该信息准则须是一致估计。AIC和GAIC均不属于一致估计，MDL是一致估计，因此，可以使用FDC准则改造MDL算法。此外，经GLE改进的GMDL也属于一致估计，且GMDL在子带个数估计方面性能要好于MDL，所以考虑结合GMDL算法和FDC准则对WSS算法进行改进，即：

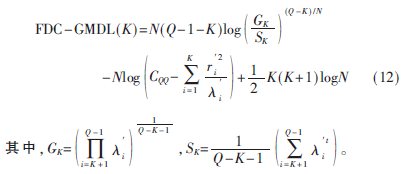
　　以上提出的基于FDC的GMDL宽带频谱感知算法不需要设置门限或估计噪声功率，从而避免了不准确估计的干扰，具有更好的鲁棒性。FDC算法只是在MDL和GMDL算法基础上的改进，算法的复杂度并没有很大的提高。同时，由于灵活系数的灵活调节，基于FDC的宽带频谱感知在估计PU占用子带个数和感知性能这两个方面有很强的适应能力，因此，在实际应用中具有很高的价值。

　　类似地，由式(11)和式(12)得到相应的判决方程：

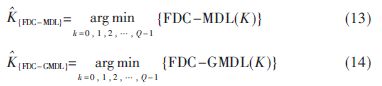
3 仿真结果及分析

　　利用MATLAB仿真，设定LFB子带总数Q=64，K=20，灵活系数t=1.9。与ISTT、AIC、MDL、GAIC、GMDL、GBIC[4]等宽带感知算法进行性能比较。在仿真中，为了满足实际应用要求，对于ISTT检测，固定期望的虚警率RFA=0.1，考虑噪声不确定度 dB两种情况。

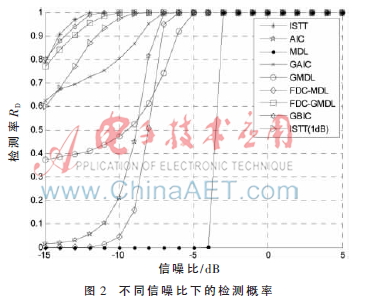
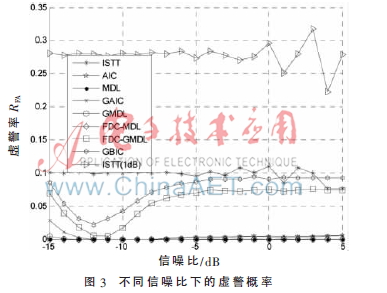
　　仿真1 取采样次数为10 000，图2和图3分别反映了在不同的信噪比下各个WSS算法的检测概率RD和虚警概率RFA的变化曲线。

　　从仿真结果可以看出，ISTT感知算法性能在时相对较好，但是?驻=1 dB时，RFA很高；AIC、MDL算法的检测性能受SNR影响较大，只能在一定的SNR区间上才能达到较好的性能；GAIC和GMDL算法的RFA比较低，同时它们的RD比AIC和MDL算法高很多；经FDC改进后，FDC-GMDL和FDC-MDL算法的性能较原算法都有比较大的提高；GBIC算法的RD稍高于FDC-GMDL算法，因为GBIC算法包含了更为丰富的统计信息，同时，这也导致了GBIC算法的复杂度要高于FDC-GMDL。此外，从虚警率的性能来看，FDC-GMDL算法的性能较大程度地优于GBIC算法。

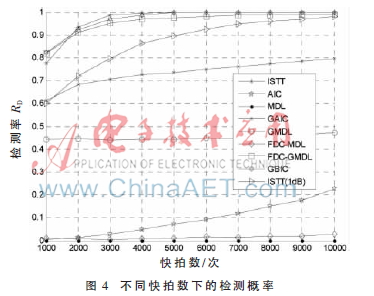
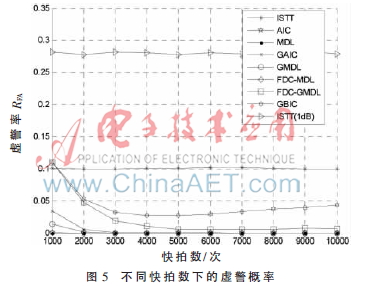
　　仿真2 图4和图5反映了SNR为-10 dB时，不同快拍数下检测概率和虚警概率的变化曲线。

　　从仿真结果可见，ISTT算法性能在噪声不确定时检测性能很差。虽然AIC算法的RD随快拍数增加而增大，但是即使快拍数达到10 000时其RD仍太低。MDL、FDC-MDL的RFA很低且接近于0，但是RD也很低，难以满足实际要求。改进的GAIC和GMDL算法的性能在原来的基础上都有了较大提升。随着快拍数的增加，FDC-GMDL感知算法的RD稳定增加，感知性能较GMDL提升明显。GBIC和FDC-GMDL算法都拥有良好的感知性能，但FDC-GMDL算法的复杂度要低于GBIC感知算法，并且FDC-GMDL算法可以改变灵活系数的值以适应不同感知系统要求。

　　仿真表明，FDC可以明显地改善MDL算法的检测性能。经GLE改进的GMDL算法符合一致估计，将FDC应用于GMDL算法，推导出的FDC-GMDL算法性能也远好于GMDL算法，即使在SNR很低的情况下，FDC-GMDL算法也能有很好的检测性能。

　　为了说明检测率和虚警率随灵活系数的变化情况，假设N为2 000，SNR为-10 dB，仿真FDC方案在不同的灵活系数下的宽带感知性能。

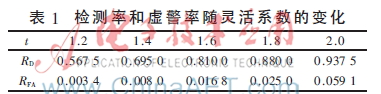
　　从表1可以看出，检测率和虚警率随灵活系数的增大而增大，因此，可以根据系统的实际要求选择相应的灵活检测系数。

4 结论

　　本文提出了基于FDC准则的WSS算法，以此为基础，结合GLE定理，提出了改进的FDC-GMDL宽带频谱感知算法。理论分析及仿真结果证明，该算法不但能够解决能量检测算法依赖噪声功率等先验信息的问题，而且可以改变灵活系数以适应系统的不同要求，具有很强的可实现性和实际应用价值。

参考文献

　　[1] MITOLA J.Cognitive radio for flexible mobile multimedia communications[C].IEEE International Workshop on Mobile Multimedia Communications，1999：3-10.

　　[2] Quan Zhi，Cui Shuguang，SAYED A H.Optimal linear coo-peration for spectrum sensing in cognitive radio networks[J].IEEE Journal of Selected Topics in Signal Processing，2008，2(1)：28-40.

　　[3] Wang Rui，Tao Meixia.Blind spectrum sensing by informa-tion theoretic criteria for cognitive radios[J].IEEE Trans-actions on Vehicular Technology，2010，59(8)：3806-3817.

　　[4] 申滨，王平玉，程克非，等．基于GBIC准则的认知无线电宽带频谱感知[J]．北京邮电大学学报，2015，38(2)：86-91.

　　[5] WAX M，KAILATH T.Detection of signal by information theoretic criterion[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1985，33(2)：387-392.

　　[6] 赵友轩，朱世磊，胡捍英．信息论准则的频谱感知技术[J]．电子技术应用，2013，39(4)：83-86.

　　[7] Qing Haobo，Liu Yuanan，Xie Gang.Robust spectrum sensingfor blind multiband detection in cognitive radio systems：a Gerschgorin likelihood approach[J].KSII Transactions on Internet and Information Systems，2013，7(5)：1131-1145.

　　[8] WU H T，YANG J F，CHEN F K.Source number estimatorsusing transformed Gerschgorin radii[J].IEEE Transactions onSignal Processing，1995，43(6)：1325-1333.

　　[9] Lu Zhihua，ABDELHAK M Z.Flexible detection criterion forsource enumeration in array processing[J].IEEE Transactionon Signal Processing，2013，61(6)：1303-1314.