文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.11.038
中文引用格式: 晋良念,钱玉彬,申文婷,等. 基于改进OMP的超宽带穿墙雷达稀疏成像方法[J].电子技术应用,2015,41(11):135-139.
英文引用格式: Jin Liangnian,Qian Yubin,Shen Wenting,et al. Sparse imaging for ultra-wideband through-the-wall radar based on modified OMP algorithm[J].Application of Electronic Technique,2015,41(11):135-139.
0 引言
穿墙雷达成像(Through the Wall Radar Imageing,TWRI)使用电磁波穿透墙体和内部封闭的建筑物进行监测,以确定建筑结构布局,区分建筑物内部的活动情况,检测、识别和跟踪运动目标。TWRI技术在搜救、墙后目标检测和城区环境的监视等方面备受关注[1-4]。TWRI系统通常利用超宽带信号和大孔径天线阵列提供高的距离向和方位向分辨率,能够在较短的采样时间内利用较小的存储空间获得高质量图像,与之对应的后向投影一类算法需要大的空间和时间(或频率)采样数据才能获得高质量成像。
近年来,压缩感知理论的兴起,国内外学者将该理论很好地应用到TWRI中,提出了一些高分辨稀疏成像方法[5-6]。它们首先将成像区域划分为有限个网格,当目标恰好落在网格点上,稀疏成像效果很好。一旦目标偏离了网格点,基矩阵不匹配,从而引起成像模糊,甚至散焦。为此,文献[5]通过建立off-gird稀疏表示模型,提出了一种基于L21范数惩罚项的FISTA算法,该算法虽能较准确地恢复目标散射系数,但是算法的性能受人工参数设置的影响,在实际应用中很难正确地选择。文献[6]针对穿墙雷达偏离网格目标成像中提出了一种贝叶斯推理方法,克服了FISTA算法性能受人工参数设置的影响。但是,该方法在成像区域划分网格数过大时处理速度会很慢,所以需要寻求新的方法提高处理速度。
本文提出一种改进的正交匹配追踪方法(GBTOMP算法)实现偏离网格目标超宽带穿墙雷达稀疏成像。该方法以正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法为基础,先通过最速上升梯度优化方法搜索到目标的真实位置,逐渐减小网格偏移量,修正模型中的感知矩阵,再由修正的感知矩阵通过最小二乘方法计算目标散射系数,但在此计算过程中,会引入冗余下标。本文利用贝叶斯假设检验去冗余,这样既可以减小重构过程的运算量,还可以增强重构的精度和抗噪性能。仿真和实验结果验证了本文方法的有效性和可行性。
1 稀疏表示模型

一般的穿墙传播模型可以等效为如图1所示的两层传播模型[7]。假设均匀介质墙体的厚度为d,相对介电常数为?着。将成像区域在方位向和距离向上离散成Nx Ny个网格点,对应的像素值用?滓k,l,k=1,…,Nx,l=1,…,Ny表示,当网格点有目标时k,l不为0,反之k,l等于0。为了方便表示,将k,l按照顺序重新排列成Nx Ny维的目标散射系数列向量,令所有元素的网格位置用矩阵表示,其中的元素用p=[xp,yp]T表示,对应的像素值用p表示,则第n个天线回波信号的离散数据模型为:

式中,yn=[yn(t1),…,yn(tM)]T,An为M×Nx Ny的矩阵,第m行的元素为[s(tn,m-n,1),…,s(tn,m)],这里n,p为第n个天线到第p个网格点之间的传播时延。
根据图1所示的传播模型,n,p可以近似表示为:
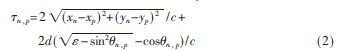
式中,xn、yn分别表示天线的坐标位置,n,p为传播的入射角,当成像区域距离天线较远时可以近似为:
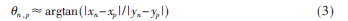
将N个天线到成像区域中所有像素点的传播时延按照式(2)和式(3)来计算,并把所有天线的接收数据进行堆叠,由此所构造的离散数据模型为:

然而,实际情况中目标很可能偏离预设网格,如图1所示,这种偏移会影响A′的精确计算。定义成像空间所有网格的偏移量矩阵为,A′关于的函数为A′。另外,对于穿墙成像场景来说满足稀疏特性,因此可以利用较少的测量值恢复。令表示从y中随机选择选择Q1个天线单元和每个天线单元随机选择Q2个数据得到的Q1Q2个数据矢量,并定义这种随机选择形式构成的测量矩阵用表示[8],由此得到大小为Q1Q2×1的测量数据(或稀疏成像)模型(为了书写方便将A为:
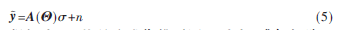
根据式(5)的稀疏成像模型可以看出,感知矩阵A有关,因此求解式(4)反演需要事先准确估计?专参数。当且仅当A满足约束等距性质时,可以通过求解如下优化问题将高维信号从低维的测量值中准确重构出来。
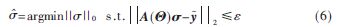
由于最小0范数问题是一个非确定性多项式难问题,目前的重构算法都是基于0范数的变换或逼近处理,其中贪婪算法以其运算速度快,实现简单的优势被用于穿墙雷达成像中。
2 GBTOMP的稀疏成像方法
2.1 GBTOMP算法
本文提出的GBTOMP算法是在正交匹配追踪算法[9]的迭代过程中采用梯度优化最速上升算法校正网格偏移量,然后采用贝叶斯假设检验[10]剔除冗余下标。该算法整体上可以分为两大步:第一,根据残差与感知矩阵的内积最大值找到最匹配原子位置(预设网格位置)。由于目标可能会偏离预设的网格位置,因此在该位置需要进行梯度优化的最速上升,以搜索到目标的真实位置,从而以目标真实位置建立新的感知矩阵,并由该矩阵利用最小二乘法求得散射系数向量的近似值,同时通过交替迭代更新下标集求解来得到目标散射系数。第二,OMP算法在有噪声和没有噪声的情况下都会存在冗余下标问题。为解决此问题,GBTOMP算法最后采用贝叶斯假设检验理论给出判决准则对第一步输出的预选下标集中原子进行筛选,得到等于或者大于信号真实下标集估计后,再用最小二乘算法进行重构,以改善算法的性能,增强其抗噪能力。GBTOMP算法流程如下。
初始化:构造测量向量,网格偏移矩阵,感知矩阵A。
(1)采用OMP算法找到匹配原子对应的空间网格位置,利用最速上升梯度优化方法对偏离网格进行估计,再利用最小二乘法对目标散射系数进行粗估计,输出预选下标集P和粗重构目标散射系数X。
(2)从预选下标集P出发,通过贝叶斯假设检验准则设置一个适当门限Thj对P中的元素进行筛选,将大于门限的元素都保留在最终的下标集F中。
输出:根据最终下标集F,利用最小二乘法得到目标散射系数最终的估计值。
2.2 网格偏移量的估计
在GBTOMP算法的迭代过程中需要估计网格偏移量,其代价函数的构造是关键。OMP算法是以测量数据和感知矩阵A构造代价函数的。为了能够使得估计准确,并使处理过程更加稳定,本文使用OMP算法相关函数的平方开方项来表示[11]:
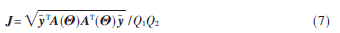
首先初始化迭代更新次数k=1,残差向量r。计算感知矩阵A所有列和残差向量r的内积值,找到内积值最大时所对应的列下标pk,接着进入搜索目标真实位置过程,满足搜索条件|Ji-Ji-1|<a结束,这里的i代表搜索过程中的迭代次数,a代表很小的一个正数。在此过程中,从?仔中取出第pk列赋给?仔0,以该点坐标(xp,yp)计算出与随机选择Q1个天线组成新集合的第q个索引号天线位置之间的双程传播时延为:
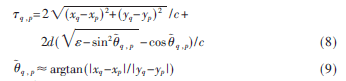
为求解代价函数J关于所选择坐标(xp,yp)的梯度,需要事先求解?子q,p关于(xp,yp)的偏导,分两种情况进行:
(1)当xq=xp时,即q,p=0,q,p简化为:
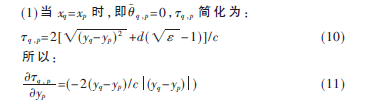
(2)当xq≠xp时,即q,p≠0,q,p关于xp和yp的偏导数为:

假设辐射脉冲波形为高斯脉冲s(t),则第q个天线和所选目标坐标(xp,yp)对应的感知矩阵Aq、B是大小为Q2×1的矩阵,它们的第q2行分别为:

式中是当前(xp,yp)对应的感知矩阵,仅仅是A的一个子集,这样处理是为了提高运行速度,减小存储空间。B1x和B1y表示对矩阵分别关于xp和yp的偏导数,它们的具体表达式与s(t)有关。以梯度搜索方法更新所选空间的坐标为:

式中是搜索步长,本文中以网格尺寸为参考的很小的正数。由此得到更新后的重新计算代价函数Ji,搜索迭代次数i=i+1,一旦代价函数满足条件|Ji-Ji-1|<a就终止搜索过程。终止后,将所选的网格空间位置?仔1所对应的感知矩阵保存在A2矩阵中,同时将所选的感知矩阵列下标pk添加到预选下标集P中,由A2通过最小二乘法计算出第k次粗估计的散射系数xpre,并更新残差向量。

继续搜索下标并校正网格偏移量,如此循环迭代,k=k+1,直到残差向量r满足条件,粗估计结束。将k次循环求得的散射系数xpre对应其下标集P赋给Nx Ny维列向量X。
X{P}=xpre(18)
2.3 贝叶斯假设检验去冗余
为剔除OMP算法输出的预选集P中的冗余下标,根据贝叶斯假设检验模型[10]构造似然函数,其似然比检验公式为:
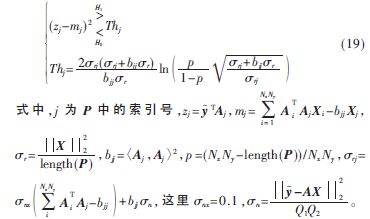
根据判决准则可知,当(zj-mj)2>Thj时,下标j对应的散射系数?滓j的值为非零,更新此时的j为最终下标,反之,下标j对应的散射系数?滓j为零,则从预选下标集中剔除此时的j值。对预选下标集中元素进行筛选,最终剩下的真实下标集为F,接下来利用最小二乘法进行目标散射系数重构完成整个GBTOMP算法。
3 仿真与实验结果分析
3.1 仿真结果分析
利用GPRMAX产生仿真数据[12],发射信号采用高斯脉冲,脉冲中心频率为1 GHz。墙体厚度为0.20 m,相对介电常数为6,电导率为0.03 S/m。
场景1:天线阵列由16个收发共置单元组成,随机选择其中的10个天线单元,阵元间距为0.1 m。成像区域是[-1 m,1 m]×[0.3 m,1.3 m],距离向和方位向的网格尺寸均为0.05 m。假设成像区域中有三个点目标,其坐标分别为(-0.414 m,0.514 m),(0.025 m,0.725 m),(0.325 m,0.965 m)。图2为OMP方法和本文GBTOMP方法成像结果。从图2(a)可以看出,OMP方法成像出现严重散焦,同时带来虚假像,从图2(b)可以看到,估计的目标位置和预设目标位置完全吻合,同时目标像聚焦程度高,很明显本文方法性能优于传统OMP方法。

场景2:天线阵列由45个收发共置单元组成,随机选择其中的10个天线单元,阵元间距为0.04 m,与墙体之间的距离为0.2 m。图3给出了2维GPRMAX模型,图中左边的长方形目标中心位于(0.7 m,3.25 m),长为0.4 m,宽为0.3 m,右边的圆形目标体的中心位置位于(1.25 m,3.05 m),半径为0.2 m。GPRMAX网格单元尺寸为0.005 m,采样时窗为30 ns。假设回波信号由有目标时减去无目标时的信号进行模拟。

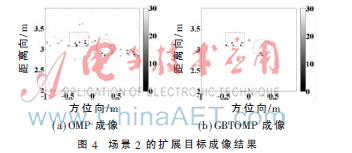
图4给出了两个扩展目标的成像结果,成像区域的方位向和距离向的网格尺寸设为0.03 m。图中的矩形和圆形虚线框代表两目标的真实位置。从图4可以看出,传统OMP方法的成像效果较差,虽然能够大致识别目标位置,但是引入了很多的虚假目标像,而本文方法GBTOMP成像效果明显改善,目标像清晰。
3.2 实验结果分析

使用美国GSSI公司的探地雷达SIR-20搭建穿墙实验场景,如图5所示。实验墙体为实心砖墙,墙体厚度0.20 m,相对介电常数6.4。选用1 GHz的喇叭天线,架高1.2 m,贴着墙体。水平移动喇叭天线共扫描21个测点,数据处理时随机选择10个测点,测点间距为0.05 m,合成孔径长度为1 m,要求在每个天线孔径测试点处测量2次,包括有人和无人的场景。人体目标高度为1.80 m,体型宽度约0.40 m,站在墙后1 m处。SIR-20系统数据采集的参数设置:每道采样1 024点,每秒60道,时间窗15 ns。

首先将SIR-20系统采集的数据波形做平均处理,然后经过去噪和杂波相消、自动增益控制等信号处理得到较好的目标回波,所有成像都是以天线阵列中心为坐标原点。图6给出实验数据成像结果比较,图中的矩形虚线框代表目标的真实位置。从图中可以看出,传统OMP方法目标成像散焦现象较严重,目标区域不能确定,且周围还有较多的虚假像。而本文GBTOMP方法成像则不同,杂波相对较少,且目标位置清晰可见,由此看来通过校正目标偏离网格能够很好解决传统稀疏成像所出现的散焦现象。
4 结论
本文提出的GBTOMP稀疏成像方法,交替迭代得到目标真实空间位置和目标散射系数,目标位置的校正保证了基矩阵的匹配,实现目标的高质量稀疏成像。仿真和实测数据处理结果表明:与OMP成像相比,本文GBTOMP方法成像效果在目标位置准确度还是目标聚焦程度有明显的提高。但是,由于以点稀疏模型对扩展目标进行成像,存在图像不够平滑,也不连续等问题,下一步工作将对扩展目标的稀疏成像方法展开研究。
参考文献
[1] TIVIVE F H C,BOUZERDOUM A,AMIN M G.A subspaceprojection approach for wall clutter mitigation in through--wall radar imaging[J].IEEE Transactions on Geoscienceand Remote Sensing,2015,53(4):2108-2122.
[2] LI G,BURKHOLDER R J.Hybrid matching pursuit for distributed through-wall radar imaging[J].IEEE Transactionson Antennas and Propagation,2015,63(4):1701-1711.
[3] 蒋留兵,韦洪浪,许腾飞,等.EEMD生命探测雷达人体数量识别技术[J].电子技术应用,2014,40(5):122-125.
[4] LIU J,CUI G,JIA Y,et al.Sidewall detection using mul-tipath in through-wall radar moving target tracking[J].IEEEGeoscience and Remote Sensing Letters,2015,12(6): 1372-1376.
[5] XIA S,LIU F.Off-grid compressive sensing through-the-wall radar imaging[C].SPIE Defense+Security.International Society for Optics and Photonics,2014:90771F-90771F-8.
[6] 晋良念,钱玉彬,刘庆华,等.超宽带穿墙雷达偏离网格目标稀疏成像方法[J].仪器仪表学报,2015,36(4).
[7] JIN T,CHEN B,ZHOU Z.Imaging-domain estimation of wall parameters for autofocusing of through-the-wall SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(3):1836-1843.
[8] LAGUNAS E,AMIN M G,AHMAD F,et al.Joint wall mitigation and compressive sensing for indoor image reconstruction[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(2):891-906.
[9] 李少东,裴文炯,杨军,等.贝叶斯模型下的OMP重构算法及应用[J].系统工程与电子技术,2015,37(2).
[10] 甘伟,许录平,苏哲,等.基于贝叶斯假设检验的压缩感知重构[J].电子与信息学报,2011,33(11):2640-2646.
[11] GURBUZ A C,TEKE O,ARIKAN O.Sparse ground-penetrating radar imaging method for off-the-grid target problem[J].Journal of Electronic Imaging,2013,22(2):021007-021007.
[12] XIE J L,XU J L.Ground penetrating radar-based experimental simulation and signal interpretation on roadway roof separation detection[J].Arabian Journal of Geosciences,2014:1-8.

