0 引言

　　无线传感器网络(Wireless Sensor Networks，WSN)是由多个传感器节点、汇聚节点和终端组成并协作感知、采集和处理网络覆盖区域内的各种环境参数或监测对象信息，然后将逻辑上的信息转化为现实物理信息。覆盖问题是无线传感器网络研究的热点问题之一，其目的是用尽可能少的传感器节点和能量来完成对目标区域的监测。目前对于在二维平面上覆盖控制的研究比较成熟，但是在实际应用中，绝大多数情况下需要在三维监测区域中放置传感器节点，为了在保证网络连通的情况下有较高的覆盖率，某些关键区域需要放置多个传感器节点来保证采集数据的准确性。

1 相关工作

　　无线传感器网络K重覆盖主要是研究传感器节点位置布置的问题，目前的研究主要集中在二维平面[1-4]，然而实际应用中通常需要在三维空间中部署传感器节点，因此本文研究的是三维空间中传感器K重覆盖的问题。

　　三维空间K重覆盖，按照监测区域的应用要求可分为整个监测区域的K重覆盖和关键区域的K重覆盖。文献[5]提出基于空间镶嵌的三维无线传感器网络K覆盖机制，从覆盖冗余率、节点度两个方面，比较得出截角八面体是最佳的填充单元。该文献还提出了解决空洞覆盖的算法和相邻填充单元协作修复算法，进一步延长了网络的生命周期。文献[6]提出了一种基于概率和网络最坏情况覆盖的三维传感器网络节点K覆盖方法，该方法与原基于概率的K覆盖方法比较，能用较少的节点满足相同的覆盖度。文献[7]主要研究的是在三维空间中利用规则多面体的填充特点，并计算了单位节点最大的有效体积，根据最小体积计算方法得到了目标区域保持充分覆盖且相邻节点相连接时所需要的最少节点数，最终得到最优的填充多面体。文献[8]利用鲁洛四面体来实现三维目标区域的K重覆盖，估算出相应的最小传感器节点的空间密度，并且证明了一个鲁洛四面体区域如果至少包含K个传感器则能保证该鲁洛四面体区域被K重覆盖。

2 覆盖机制

　　2.1 问题定义

　　2.1.1 假设条件

　　(1)无线传感器网络始终是连通的；

　　(2)节点一旦部署后，位置基本保持不变，即节点移动距离与节点感知半径或通信半径相比可以忽略；

　　(3)相对于节点感知半径而言，监控区域足够大，区域边界效应可以忽略；

　　(4)网络监测目标区域是长、宽、高均为L的立方体。

　　2.1.2 感知模型

　　节点的感知模型采用布尔感知模型（即0-1感知模型）。假设在三维空间中有一个传感器节点nodei(xi，yi，zi)，空间中任意一个探测点p(x，y，z)，则节点和探测点间的欧氏距离为：

　　从式(1)可以看出，若传感器节点nodei与探测点p之间的欧氏距离小于传感器节点的感知半径Rs则能被覆盖，否则不能。

　　2.1.3 K覆盖的定义

　　给定一个传感器节点集合S，节点感知半径Rs和监测区域A，如果A中每个点都被S中的至少K个传感器所覆盖，则整个监测区域被K重覆盖。

　　2.1.4 覆盖冗余率和空间密度

　　空间覆盖冗余率：

　　式(2)中，Vall表示传感器节点覆盖的总体积，Vtarget表示覆盖的有效体积。

　　空间密度：

　　式(3)中，K表示覆盖重数，V单元表示单个多面体的体积。

　　2.1.5 形式化定义

　　综合2.1.4中公式的定义，本文覆盖问题定义如下：

　　式(4)中，在目标区域体积一定的前提下，为了得到最小的覆盖冗余率，需要得到所有传感器节点的最小覆盖体积，即用最少的传感器节点覆盖目标检测区域。式（5）中，在覆盖重数一定的情况下，需要使覆盖单元的体积最大才能得到最小的空间密度。在用最小的覆盖冗余率和最小的空间密度的情况下用最少的传感器节点来达到覆盖的目的，从而最大程度减少节点部署数目，节约成本。

　　2.2 确定性覆盖下的重覆盖

　　2.2.1 几种覆盖方式冗余度的比较

　　(1)将三维目标监测区域划分为多个无缝堆砌的多面体，传感器节点的传感半径为多面体填充单元的外接球直径。具体做法是将传感器节点放置在空间填充多面体的顶点上，保证多面体能被完全覆盖。

　　(2)计算覆盖冗余度来选择最佳的覆盖方案：

　　冗余率：

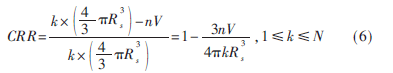
　　其中，n表示每个顶点相连的填充单元个数，V表示单个填充单元的体积，N表示填充单元顶点的个数。

　　(3)比较立方体、六角棱柱、截角八面体的覆盖冗余率

　　①立方体由8个顶点、6个正方形和12条边组成，在填充空间时，每个顶点可以与8个立方体（包括自身的立方体）相连，则立方体的边长a=Rs/3，立方体的体积V=a3=R/9。

　　②六角棱柱有12个顶点、2个正六边形、6个矩形和18条边组成，在填充空间时，每个顶点可以与6个六棱柱相连，令正六边形的边长为a，矩形的边长为a，则边长a=Rs/6，六角棱柱的体积为V=R/4。

　　③截角八面体由24个顶点、8个正方形、6个正六边形和36条边组成，在填充空间时，每个顶点可以与4个截角八面体相连，令正方形和正六边形的边长为a，则a=Rs/10，截角八面体体积是V=4R/25。

　　由式(6)覆盖冗余率可知，单个填充单元体积V越大，CRR越小，所以可以看出截角八面体是最佳的选择。

　　2.2.2 最优覆盖时填充单元个数

　　令三维空间每个维度上所需要的截角八面体的个数为m，填充整个空间所需要的截角八面体的数量为M，L表示目标区域的边长。　

　　首先根据目标区域的大小和传感器节点的感知半径，通过式(8)和式(9)计算填充目标区域所需截角八面体的个数，然后将节点均匀地放置在截角八面体的顶点上，随机选取K个节点进入工作状态，从而实现网络的K重覆盖。

　　2.3 随机覆盖下的K重覆盖

　　2.3.1 随机覆盖的方法

　　采用随机节点覆盖策略，随机均匀地将适量的传感器节点以及少量的汇聚节点部署在目标监测区域内。传感器节点的数量可以根据目标区域的大小A、传感器节点的传感半径Rs和覆盖重数K大致的算出来：

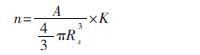
　　为了提高目标监测区域覆盖率，应该在目标检测区域部署大于n个传感器节点，一般部署N个节点：n<N≤2n。所有传感器节点的初始状态都为工作状态，并向汇聚节点发送各自的位置信息。为了确保目标区域的K重覆盖，将目标区域划分为若干个无缝堆砌的多面体，只要各个多面体均被K个传感器完全覆盖，则能保证整个目标监测区域被K重覆盖。如果只是在各个多面体内部放置K个以多面体外接球直径为传感半径的传感器节点，传感器节点的空间密度为：

　　因此这样会造成节点过度的冗余。为了减小不必要的冗余，本文的方法是使多面体外接球重叠部分中的传感器节点保持工作状态，其余节点休眠，这样重叠区域中的每个传感器节点可以保证至少两个多面体被覆盖，传感器节点的空间密度最大为：

　　这样会很大程度上减小节点密度。各种多面体的重叠区域如图1和图2所示。

　　2.3.2 几种覆盖方式空间密度的比较

　　(1)立方体的6个面都是等大的正方体，所以6个面上都有等大的重叠区域，假设一个立方体各个面上重叠区域中工作节点的个数分别为a1，a2，…，a6，其中a1+…+a6=K，所以：

　　(2)六棱柱是由6个矩形和2个正六边形组成，假设6个矩形面的重叠区域中工作节点的个数分别为：a1，…，a6，两个正六边形面的重叠区域中工作节点的个数分别为：b1，b2，。其中，a1+…+a6+b1+b2=K。所以，如果填充多面体是六棱柱，则传感器节点的空间密度为：

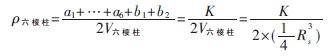
　　(3)截角八面体是由8个正方形、6个正六边形，假设8个正方形面的重叠区域中工作节点的个数分别为：a1，…，a8，6个正六边形面的重叠区域中工作节点的个数分别为：b1，…，b6。其中，a1+…+a8+b1+…+b6=K。所以，如果填充多面体是截角八面体，则传感器节点的空间密度为：

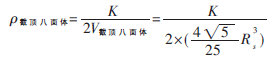
　　2.3.3 鲁洛四面体

　　为了和2.3.2中几种常见多面体比较空间密度值，下面介绍一个比较特殊的多面体，鲁洛四面体（Reuleaux tetrahedra）。

　　图3中，四个球体中心连线所构成的边构成一个正四面体，四个球体交集构成的形体叫做鲁洛四面体，表示为RT(r)。根据文献[8]，如果监测区域中任何鲁洛四面体中含有不少于K个传感器节点，则该网络的感知覆盖重数可保证为K。鲁洛四面体的体积公式：

　　三维区域中完全K重覆盖的最小传感器节点密度为：

　　连接鲁洛四面体四个顶点组成的是一个规则的正四面体，如图4，该正四面体的体积为：

　　可以看出鲁洛四面体的4个边缘（鲁洛四面体减去正四面体）的体积为：

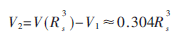
　　每个边缘的体积为：

　　V3=V2/4≈0.076R

　　两个鲁洛四面体叠加在一起的情况如图5，则这两个鲁洛四面体的体积为：

　　V4=2V(R)-2V3≈0.692R

　　可以计算出填充多面体是鲁洛四面体时，传感器节点的空间密度为：

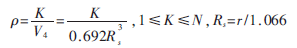
　　然而实际应用中，不可能把一个三维区域完全分解成多个鲁洛四面体相互叠加，并使鲁洛四面体与该三维目标区域边界相近。因此，需要部署稍微多些传感器节点以保证在包含边界区域在内的所有监测区域范围内均实现K重覆盖。

3 随机部署中工作节点选择机制

　　3.1 模型的描述

　　节点的覆盖策略：node〈i，j，state〉，0≤i≤M，0≤j≤24，state=-1，0，1，其中i表示填充单元的编号，j表示节点所在填充单元的顶点编号，M表示填充单元总数，state表示节点状态，-1表示节点剩余能量低于工作阈值而处于失效状态，0表示节点处于休眠状态，1表示节点处于工作状态。

　　3.2 选择流程

　　(1)首先将三维目标区域A划分为若干个多面体A=(A1，A2，A3，…，AN)，N为多面体的个数，相邻多面体的外接圆相交，第一个多面体和它邻近的多面体的外接球的重叠区域表示为S1=(a11，a12，…，a1n)，n为相邻多面体面的个数,所有的重叠区域可以表示为S=(S1，S2，…，SN)。

　　(2)初始状态下各个传感器节点处于工作状态，每个传感器节点向Sink节点发送各自的位置信息。

　　(3)如果有传感器节点落在多面体Ai的重叠区域Si中，统计区域Si中传感器节点的个数numi。

　　(a)如果numi>K，休眠K-numi个传感器节点和多面体内部不重叠区域的传感器节点；

　　(b)如果numi<K，在多面体内部选择numi-K个传感器节点为工作节点，其余节点进入休眠状态。

　　(4)如果i<N，转(3)；否则，节点选择完毕。

　　3.3 空洞修复策略

　　因为节点能量有限，有些节点会失效，需要一个填充单元内部的空洞自修复。具体做法是：

　　(1)节点正常工作所需的能量阈值为Emin，计算覆盖监测区域所需填充单元的个数为M；

　　(2)每隔时间间隔T，对监测区域中传感器节点的state进行重新检测：若第i个多面体中第j个节点的state为1且剩余能量E<Emin，则该节点进入失效状态，令state=-1且M=M-1；

　　(6)若i<Ｍ，转（3）；否则，自修复完毕。

4 仿真结果

　　本文利用MATLAB仿真软件对比了以立方体、六棱柱、截角八面体，鲁洛四面体为填充多面体的三维目标监测区域，确定性部署中覆盖冗余率和随机部署中传感器节点空间密度。

　　4.1 确定性部署中覆盖冗余度的比较

　　图6是确定性部署中覆盖冗余度的比较，传感器节点被确定放置在每个填充多面体的顶点处。从中可以看出覆盖重数K较小时，以截角八面体为填充多面体的目标区域的覆盖冗余率最低，随着覆盖重数的增加，以几种多面体填充的目标监测区域的覆盖冗余率都有大幅度增加并且目标区域的覆盖冗余率都趋于相近。

    4.2 随机部署中传感器节点的空间密度的比较

　　图7是随机部署中传感器节点的空间密度的比较，传感器节点被随机部署在三维目标监测区域中，将目标监测区域划分为若干个多面体，使部署在各个多面体外接球重叠部分的传感器节点成为工作节点。从图中可以看出截角八面体的传感器节点的空间密度最小，随着覆盖重数的增加，各个多面体对应的目标区域的传感器节点的空间密度也随之增加，立方体对应的传感器节点的空间密度增加最快，截角八面体最慢，可以看出截角八面体对应目标区域传感器节点的空间密度最低，所以截角八面体是最佳的选择。

　　4.3 改进的空洞修复策略

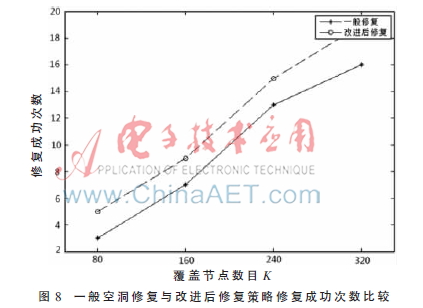
　　图8是随机布置节点后，假设覆盖重数为2时一般的空洞修复算法与改进后的空洞修复算法比较，可以看出改进后的策略修复成功的次数高于一般的空洞修复策略。

5 结论分析

　　针对三维无线传感器网络K重覆盖的问题，本文分别从确定性覆盖和随机覆盖两个方面来研究。在确定性覆盖中，分别以立方体、六棱柱和截角八面体作为填充单元，把节点部署在各填充单元的顶点并以填充单元的外接球直径为传感半径，通过比较覆盖冗余度，得出截角八面体是最佳的选择。在随机覆盖中，先将节点随机部署在三维目标区域中，然后根据选择工作传感器节点的机制，使一些节点进入激活状态，其余节点进入休眠状态，最后比较了传感器节点的空间密度值。实验显示，截角八面体是最佳选择。提出了随机部署中选择工作传感器节点的机制和改进的空洞修复协议。下一步工作将研究在本文提出的随机部署中，工作节点的选择机制。即随着节点能量的消耗，针对网络覆盖空洞，提出一些空洞修复的优化算法。

参考文献

　　[1] FEI X，BOUKERCHE A，YU R.A pomdp based K-coveragedynamic scheduling protocol for wireless sensor networks[J].GLOBECOM 2010，2010 IEEE Global Telecommunications Conference，2010：1-5.

　　[2] 韩志杰，吴志斌，王汝传.新的无线传感器网络覆盖控制算法[J].通信学报，2011，32（10）.

　　[3] SIMON G，MOLN?魧R M，G?魻NCZY L，et al.Dependable k-coverage algorithms for sensor networks[C].Instrumentation and Measurement Technology Conference Proceedings，2007.IMTC 2007.IEEE.IEEE，2007：1-6.

　　[4] MAO X，LIU Y，TANG S，et al.Finding best and worst k-coverage paths in multihop wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems，2013，24(12)：2396-2406.

　　[5] 王兴伟，蔡凌，黄敏.基于空间镶嵌的三维无线传感器网络k覆盖机制[J].小型微型计算机系统，2014，35(3).

　　[6] 王丽，苗凤娟，陶柏睿，等.一种改进的无线传感器网络三维K覆盖控制方法[J].河南理工大学学报：自然科学版，2014，33(3)：333-338.

　　[7] 钟永信，黄建国，韩晶.三维传感器网络部署、覆盖和连接问题研究[J].控制与决策，2011，26(10)：1447-1451.

　　[8] Ammari H M，Das S K.A study of k-coverage and measuresof connectivity in 3D wireless sensor networks[J].Computers，IEEE Transactions on，2010，59(2)：243-257.

　　[9] Nazrul Alam，Haas.Coverage and connectivity in three-dimensional networks[J].Eprint Arxiv：cs/0609069，2006.