摘 要: 针对基本果蝇优化算法在求解高维函数时存在求解精度低、迭代收敛速度较慢等问题,提出一种基于差分演化的果蝇优化算法。该算法将差分演化策略融合到果蝇优化算法中,对每代产生的群体进行变异、交叉、选择操作,增加种群的多样性,使其能更快、更有效地求解高维函数问题。对12个基准函数进行了仿真验证,结果表明,与基本的果蝇优化算法和差分演化算法相比,新算法在收敛速度、求解精度上都具有明显的优越性。
关键词: 果蝇优化算法;差分演化;多样性
0 引言
果蝇优化算法(Fruit Fly Optimization Algorithm,FOA)是一种新的全局优化进化算法[1]。该算法源于对果蝇觅食行为的模拟[2],由于该算法参数较少,结构简单,实现容易,因而一经提出便得到了一些学者的研究和应用[3-6]。然而,果蝇优化算法和其他全局优化算法一样,受参数的影响很大,也容易陷入局部最优。目前关于改善果蝇优化算法性能的研究成果相对较少,迫切需要展开更深入研究。
果蝇优化算法中所有个体都向最优的位置聚集,这一行为导致种群多样性的丢失,特别是对于高维多极值复杂优化问题,易出现求解精度低、迭代收敛速度较慢等问题。针对这一问题,本文将差分演化策略融合到果蝇优化算法中,对每代产生的群体进行若干次的变异、交叉、选择操作,从而增加种群的多样性,使其更快、更有效地求解复杂函数问题。
1 基本果蝇优化算法和差分进化算法
1.1 基本的果蝇优化算法
果蝇优化算法是一种基于果蝇觅食行为推演出的寻求全局优化的新方法。果蝇本身在感官知觉上优于其他物种,尤其是在嗅觉与视觉上。首先果蝇利用嗅觉搜集空气中的气味,然后飞向食物位置附近,再利用视觉发现食物与同伴聚集的位置,并且往该方向飞去。
依据果蝇搜索食物特性,将果蝇优化算法归纳为以下几个必要的步骤[2]:
(1)初始化种群。给定种群规模Sizepop和最大迭代数Maxgen,在搜索空间中随机初始化果蝇群体位置X_axis和Y_axis;
(2)设置果蝇个体利用嗅觉搜寻食物的随机方向与距离:
Xi=X_axis+RandValue(1)
Yi=Y_axis+RandValue(2)
式中,RandValue为搜索距离。
(3)计算个体与原点之距离Disti和味道浓度判定值Si,其值为距离Disti的倒数:

Si=1/Disti(4)
(4)将味道浓度判定值Si代入味道浓度判定函数(或称为适应度函数),求出果蝇个体位置的味道浓度Smell(i)(适应值):
Smell(i)=Function(Si)(5)
(5)找出该果蝇群体中味道浓度最佳的果蝇个体(最小化问题):
[bestSmell bestindex]=min(Smell(i))(6)
式中,bestSmell为最佳味道浓度值;bestindex为最佳位置序列。
(6)记录并保留最佳味道浓度值bestSmell与其X、Y坐标,这时果蝇群体利用视觉向该位置飞去:
Smellbest=bestSmell(7)
X_axis=X(bestindex)(8)
Y_axis=Y(bestindex)(9)
(7)进入迭代寻优,重复执行步骤(2)~(5),并判断最佳味道浓度是否优于前一迭代最佳味道浓度且当前迭代次数小于最大迭代次数,若是则执行步骤(6)。
1.2 差分进化算法
差分进化(Differential Evolution,DE)算法[7]是一种随机的并行直接搜索算法。其基本原理:对个体进行方向扰动,以达到使个体函数值下降的目的。通过对种群中两个随机选择的不同向量来干扰现有向量,得到临时种群;对临时种群进行评价,计算临时种群中每个个体的目标函数值;对临时种群进行比较、选择,选取目标函数值小的新种群。DE算法以差分策略为主要特征,不同的差分策略实现不同的变异操作。本文选取rand/1/bin策略。如下所示:
(1)变异操作。选取rand/1/bin策略。从种群中随机选择3个不同个体xp,xq,xr,则:
vi(t)=xp+F(xq-xr)(10)
式中,F为缩放因子。
(2)交叉操作。此操作可以增加种群的多样性。如下所示:
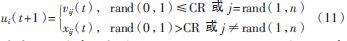
式中,CR为交叉概率,CR∈[0,1];rand(1,n)为[1,n]之间的随机整数。
(3)选择操作。由适应值函数对向量进行比较选择,如下所示:
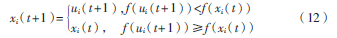
2 融合差分算法的混合果蝇算法
在果蝇优化算法迭代过程中,一旦发现最优个体,种群中的所有个体都向这个最优位置聚拢,这一特性减少了种群的多样性。如果该个体不是全局最优,极易使种群陷入局部最优。本文提出的融合差分演化的混合果蝇算法(简称DFOA),结合差分演化策略,对每代产生的群体进行若干次差分演化操作(变异、交叉、选择),增加种群的多样性,更快、更有效地求解极值。
具体步骤如下:
(1)初始化算法所需的参数;
(2)按式(1)、(2)初始化果蝇群体;
(3)按式(3)~(5)对果蝇个体进行操作;
(4)按照式(6)得到最佳的果蝇位置和最佳味道浓度值;
(5)对果蝇种群按照式(12)~(14)进行m代的差分演化操作,将得到的个体作为最佳果蝇个体;
(6)记录并保留新的最佳味道浓度值Smellbest与X、Y的坐标X_axis、Y_axis。
(7)重复执行步骤(2)~(6)的操作,直到达到最大迭代次数,或者达到目标精度要求。
从步骤(5)中可以知道,差分演化代数m可以不同。种群中差分进化代数m表明执行变异、交叉、选择操作的次数,这些操作决定了种群的变异次数,与种群的多样性有关。
3 实验及结果分析
3.1 实验设计

为了验证本文DFOA算法的性能,设计了3类测试函数:(1)DE优化实验;(2)DFOA优化实验;(3)FOA优化实验。实验选用12个常用的优化算法比较基准函数(求解最小值)。函数表达式、搜索区间、理论极值如表1所示。其中F7、F10表达式如下所示:

3.2 对比实验与结果分析
3.2.1固定迭代次数,评估算法性能
本文将迭代次数固定为1 000,函数维数为30,种群个数设置为50,差分迭代次数为10。参数F取为0.5,CR取为0.1~0.9之间的自适应交叉概率。记录DE、FOA和DFOA三种算法经过20次独立运行后,12个基准测试函数的运行结果,如表2所示。
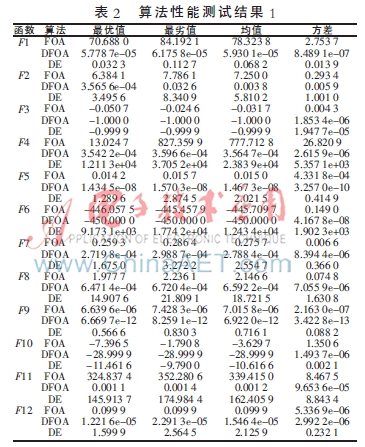
从表2中可以看出,DFOA不论是在最优值、优化均值和稳定性上都比FOA和DE算法好很多。对于复杂问题,改进的算法在精度、收敛速度上都有显著的提高。
3.2.2 差分迭代次数对算法的影响
种群中差分进化代数m表明执行变异、交叉、选择操作的次数,这些差分操作决定了种群的变异次数,与种群的多样性有关,因此关系到DFOA的性能。不同的差分迭代次数使算法的结果也不相同。参数的设置如上述所示。独立运行20次结果如表3所示。

由表3可知,m值越大,算法的收敛精度就越高,但缺点是程序执行的速度会变慢。因此,必须考虑到优化问题的复杂程度,适当选择m值。
4 结束语
基本的果蝇优化算法在寻优过程中,所有个体都向最优值聚拢,这一行为导致种群多样性的丢失,特别是对于高维复杂优化问题,易出现求解精度低、迭代收敛速度较慢等问题。针对这一问题,本文将差分演化策略融合到果蝇优化算法中,对每代产生的群体进行若干次差分演化操作,增加种群的多样性。并通过12个基准函数进行仿真验证,结果表明:相较于FOA、DE,新算法能更快、更有效地求解复杂函数问题。
参考文献
[1] PAN W T. A new fruit optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012,26(1):69-74.
[2] 潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011:10-12.
[3] XING Y F. Design and optimization of key control characteristics based on improved fruit fly optimization algorithm [J]. Kybernetes, 2013, 42(3): 466-481.
[4] LI H Z, GUO S, Li C J, et al. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm[J]. Knowledge-based systems,2013,37(1):378-387.
[5] 刘成忠,黄高宝,张仁陟,等.局部深度搜索的混合果蝇优化算法[J].计算机应用,2014(4):1060-1064.
[6] 韩俊英,刘成忠.自适应调整参数的果蝇优化算法[J].计算机工程与应用,2014(7):50-55.
[7] STORN R, PRICE K. Differential evolution—a simple and efficient adaptive scheme for global optimization over continuous spaces[J]. Technical Report, International Computer Science Institute, 1995(8): 22-25.

