摘  要： 提出了一种基于阈值的数字图像去噪算法。该算法根据椒盐噪声的特点，通过设置阈值，当待处理像素点的灰度值与该点周围像素点的均值的差小于阈值时，该像素点不作处理，否则就用该点周围像素点的均值代替该点的值。同时，研究分析了图像去噪最佳阈值与图像的平均值、方差、熵以及复杂度之间的关系，以便为快速寻找最佳阈值提供理论根据。实验仿真表明，与其他去噪算法相比，该算法既能较好地去除噪声，同时不会使图像变得模糊。

　　关键词： 数字图像去噪；椒盐噪声；选择式掩膜平滑去噪算法；最佳阈值

0 引言

　　在数字图像的产生或传输过程中，不可避免地会掺入脉冲噪声[1]。脉冲噪声的一种主要类型就是椒盐噪声。当图像被其污染时，部分像素值会发生改变，即出现灰度值较大或灰度值较小的污染点，类似白色的盐粉和黑色的胡椒末撒在图像上[2]。为了获取准确的图像信息，就要采取适当的去噪方法对图像进行处理。

　　目前国内外学者针对椒盐噪声，已经提出了许多去噪方法，比较常用的有中值滤波[3]、均值滤波、选择式掩膜平滑去噪算法等。中值滤波算法可以有效抑制椒盐噪声，且计算效率比较高，但对于高度污染的图像不能完全滤除噪声以及还原图像的边缘信息[4]；均值滤波算法虽然简单易实现，但它因为像素点取的是领域的均值而使图像变得模糊[5]，局限性很大；其他的算法如选择式掩膜平滑去噪算法，虽然在均值去噪的基础上有一定改进，但去噪效果仍不够理想。

　　本文提出一种非线性去噪算法——基于阈值的均值去噪法，只要选取合适的阈值，就会得到更好的去噪效果。该算法可以克服传统方法的缺点，尽可能只对被噪声污染的像素点进行处理，其他像素点的灰度值不变，从而不会使去噪后的图像变得模糊，保证图像的边缘信息不丢失，同时加强对点、线、尖顶细节的处理。

1 数字图像噪声特点

　　数字图像中的噪声可理解为“图像中不需要的部分，或者在一定场合没有研究价值的部分”，它主要来源于图像的产生和传输过程[6]，一般常见的有以下几种噪声：

　　（1）加性噪声。该噪声不会随着图像信号的强弱变化而变化，它的存在与图像信号无关。

　　（2）乘性噪声。乘性噪声与图像信号相关，通常随图像信号的变化而变化，如式（1）所示：

　　（3）高斯噪声。这类噪声的n维分布都服从高斯分布，在数学上具有易处理性，如式（2）所示：

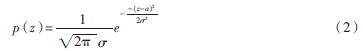
　　（4）椒盐噪声。椒盐噪声是指两种噪声，一种是盐噪声（salt noise），另一种是胡椒噪声（pepper noise），前者是高灰度噪声，后者属于低灰度噪声。一般两种噪声同时出现，呈现在图像上就是黑白杂点[7]，这种噪声是由于图像切割引起的，噪声点均匀分布于整幅图像[8]。

2 去噪方法

　　2.1 选择式掩膜平滑去噪算法

　　选择式掩膜平滑去噪算法是均值滤波的一种改进算法，考虑到均值滤波算法在消除噪声的同时，不可避免地带来平均化的缺憾，使得变化较大的线条和边缘变得模糊，且由于图像的背景与目标物体都有不同的统计特性，也就是不同的方差和均值，所以为了保持一定的边缘信息，使用选择式掩膜平滑滤波，这样可以保持图像边缘轮廓的细节。

　　选择式掩模方法取5×5的模板窗口，选取一个基准像素点，以这个像素点为基础，向四周做出图1中所示的图形，即一个正方形，四个六边形，四个五边形，一共九个屏幕窗口。分别计算各个屏蔽窗口的像素值的均值和方差，然后采用方差最小的窗口进行均值处理，如式（3）所示：

　　其中，δ是窗口中组成图形的各个像素的方差，fk是各个像素的像素值，N是组成图像的像素的个数，M是窗口中组成图形的各个像素的平均值，均值如式（4）所示。

　　2.2 基于阈值的均值去噪法

　　2.2.1 算法的实现

　　选择式掩膜平滑去噪算法虽然相比传统的去噪方法有所改进，但同样避免不了图像模糊的问题。因此本文在掩膜法的基础上提出基于阈值的均值滤波算法。一幅被椒盐噪声污染的图像中，噪声点的灰度值与其领域的均值会相差很大，应该把它滤掉；而没被污染的像素点与其领域的均值相差不大，如果选取一个合适的阈值，则该点的值可以保留。现假定一个阈值B，以3×3模板 为基准，若以a5作为待处理像素点，那么该像素点经过处理之后，均值滤波器的输出为，这样就得到了一个均值M，然后根据先前设定好的阈值B进行处理。如果|a5-M|≥B，则滤波器输出像素值A=M，即用平均值代替该点的灰度值；如果|a5-M|≤B，则滤波器输出像素值A=a5，即该点的灰度值保持不变。

　　可见，该去噪算法并不是对图像中的每个像素点都进行处理，而是有选择地保留图像原来的灰度值，从而避免破坏那些没有被噪音污染的像素点，最大限度地保留了图像的细节信息和边缘信息，使其不模糊，达到较好的去噪效果。

　　2.2.2 阈值的选取问题

　　如何选取合适的阈值对本文去噪方法的效果至关重要。如果阈值过小就退化成均值去噪法，图像会变得很模糊；如果过大也会影响去噪的效果。传统的选取阈值的方法是在滤波过程中，不断调整阈值，直到达到理想的去噪效果，效率很低。由先验知识可知，图像的不同统计参数与阈值可能存在某一特定的关系[9]，故本文在对图像去噪前，先求出相关统计参数，然后根据各个参数与最佳阈值的关系，确定一幅图像最佳阈值的大致范围，再进行小幅度的调整，便可得到最终的阈值。本文中所涉及到的四个相关统计参数分别为：图像的均值、方差、熵和复杂度。

　　为了研究这四个特征参数与最佳阈值的关系，本文采取了控制变量法。如在对均值进行验证时，选取只有均值不同，其他三个参数值基本接近的几张图像。先对这几张图像加相同点数（N）的椒盐噪声，将1~200的200个整数作为阈值B的预选取值，然后分别用本文介绍的方法去噪，通过对比信噪比PSNR，可以得到对应的最佳阈值，从而看出均值与最佳阈值的对应关系。同时可改变椒盐噪声的点数N，得到不同噪点时均值与阈值的关系。其他参数的验证方法类似。图2所示为求一张图像最佳阈值的流程图。

3 实验结果及分析

　　3.1 去除椒盐噪声的三种方法比较

　　实验中所选取的图像为256级灰度图像。图3（a）是未经处理的图像，图3（b）是对图3（a）加入椒盐噪声N=12 000的图像，图3（c）、图3（d）、图3（e）是对图3（b）分别采用均值法、选择式掩膜法和本文提出方法的去噪效果图。

　　从图3（c）可以看出，均值法的去噪效果很不理想，不但椒盐噪点没有去除干净，而且图像整体变得很模糊。图3（d）反映出选择式掩膜法去噪效果较均值法有了很大的改进，具体表现在将椒盐噪点基本去除干净，但还原出来的图像失真较大，主要是一些点、线、尖顶细节太过模糊。从图3（e）可看出，本文提出的基于阈值的均值滤波算法得到的去噪图像显然比前者效果更优，不仅基本去除了椒盐噪点，而且有效地保持图像中的重要特征和边缘信息。

　　3.2 图像相关统计参数与最佳阈值的关系

　　本文为了研究图像的特征参数与去噪的最佳阈值的关系，采用12张512×512的灰度图像，并将这12张图像分为四组，保证每一组的3张图像中只有一个参数值不同。然后利用上述控制变量法，对这3张图像分别加相同的椒盐噪点，并进行去噪处理，得到其最佳阈值。同时改变椒盐噪点数，对比在不同噪点N下的最佳阈值变化情况，得到的数据如表1所示。

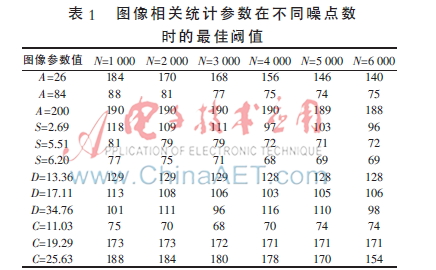
　　从表1可看出，当图像的均值A从小到大增大时，最佳阈值先减小，后增大，即均值接近0或255时，最佳阈值最大；当熵值S从小到大变化时，最佳阈值越来越小；当方差值D变大时，最佳阈值越来越小；而当复杂度C取值变大时，最佳阈值也相应变大。同时可发现，对于同一张图像，随着椒盐噪点数的增加，最佳阈值呈总体下降趋势。知道这四个参数与最佳阈值的关系后，可以根据图像的参数值快速选取最佳阈值的取值范围，然后通过微调得到最佳阈值，使去噪效果最佳。

4 结论

　　通过VC++平台的算法仿真结果表明：本文提出的基于阈值的均值滤波法，尽可能使图像不模糊，加强了对图像点、线、尖顶细节的处理，保证图像中的细节信息和边缘信息不丢失，与均值法和选择式掩膜平滑去噪法相比，去噪效果更加理想。当然该算法为了获得较好的去噪效果，所付出的时间开销也比较大，故下一步的研究重点就是提高算法效率。

参考文献

　　[1] BOVIK A. Handbook of image and video processing[M]. SanDiego： Academic Press， 2000.

　　[2] Dong Yiqiu， Xu Shufang. An efficient Salt-and-Pepper noise removal[J]. Acta Scientiarum Naturalium Universitatis Pekinensis，2006，42（5）：604-612.

　　[3] 郭海霞，解凯.一种改进的自适应中值滤波算法[J].中国图像图形学报，2007，12（7）：1185-1188.

　　[4] ZAHAVI R. Enterprise Appiication Integration with CORBA[M]. New York： JohnWiiey&Sons， 2000.

　　[5] 黄全品，王绪本.一种高效的基于阈值的图像滤波算法及其实现[J].计算机仿真，2005，22（5）：111-114.

　　[6] 王英，曾光宇.图像去噪算法研究[J].电脑与信息技术，2011，19（4）：8-12.

　　[7] 王晓凯.图像椒盐噪声及高斯噪声去噪方法研究[D].上海：复旦大学，2010.

　　[8] 唐彩虹，蔡利栋.一种基于直方图的加权均值滤波方法[J].微计算机信息，2006，（13）：209-211.

　　[9] DO M N， VETTERLI M.The contourlet transform：an efficient directional multi-resolution image rep resentation[J].IEEE Trans on Image Processing，2005，14（12）：2091-2106.