摘  要： 针对当前流行排序算法中只基于某种算法对需求进行排序而没有考虑项目实际规模的情况，提出了定性和定量分析确定需求优先级的两种思路。定性分析中研究了基于KANO模型确定优先级的方法，定量分析中以AHP算法为基础，将价值、费用、风险等多种属性的影响量化到需求优先级排序中。结合某船厂信息管理系统利用AHP方法确定需求优先级的案例讨论，验证了该需求优先级排序方法的可行性，解决了在资源有限的情况下如何确定需求优先级并分步实施的问题。

　　关键词： 需求管理；优先级；KANO层次分析

0 引言

　　目前，软件规模随着软件应用领域的拓展也在不断扩大。而各种资源的限制不可能对所有功能都完整实现，这就要求分清开发的主次顺序，使资源的利用率最优，防止项目失控。这就是需求优先级的确定过程。准确的需求已经成为软件开发项目能否成功的关键因素[1]。

　　现有需求优先级的划分方法很多，而这些方法并不通用。参考文献中关于需求优先级的排序都是基于某种特定方法，并不考虑项目本身特定属性和开发中的实际情况，考虑并不全面，存在一定弊端。本文考虑了项目的实际情况，基于软件规模大小的不同，讨论了两种确定需求优先级的方法，指出了在软件开发中确定需求优先级时存在的问题，并提出了相应算法及改进算法，同时考虑其他因素影响程度，提高需求优先级的准确性。

1 需求优先级

　　需求优先级是指软件在开发过程中需求交付的先后顺序。在实际软件开发过程中，项目管理可能会遇到以下问题[2]：新系统在开发过程中，用户有新的需求产生，而同时项目的费用和时间又固定不变；已经正式运行并处于维护中的系统，用户会针对系统中存在的问题，提出新的想法和要求，这些需求甚至可能要修改系统的整体架构[3]。这就要求项目经理在短时间内做正确的决定，首先判断该系统是否可以满足和实施这些需求[4]。其次，要权衡各种客观的约束条件，比如，能否保证项目进度，能否满足费用预算，能否合理安排人员。而在满足新需求的过程中，可能又会有新的需求。如何满足用户接踵而至的要求，既保证项目进度，又让客户满意就成了一个让需求管理者头疼的问题。这就需要项目经理将需求的优先级排序，根据排序结果依次满足[5]。

　　对于一个新的项目，首先要估算软件规模的大小，这是项目计划和控制的核心要素，也是使用哪种方法确定需求优先级的重要依据。软件规模估算方法有功能点分析法、标准组件法、模糊逻辑法、类比法、专家估算法等[6]。当前最流行的是功能点分析法，它从逻辑角度分析，依据用户需求度量软件规模，适合对需求明确的项目。对软件规模的大小做出评估后，依据软件规模大小，判断使用哪种需求优先级的排序方法，进而做出有效的选择。

2 基于KANO模型的需求优先级排序

　　在小规模项目下，可以使用定性的分析方法，该方法由项目干系人通过比较和沟通，依据某些既有原则即可确定，该方法较简便，额外成本低，更加迅捷。

　　KANO（如图1所示）是日本专家卡诺（Kano）博士提出的，是一个与产品质量相关的用户满意度模型。该模型是一个典型的定性分析模型，给出了用户需求重要性的三个层面，即基本型、期望型和兴奋型。常用于对需求指标进行分类。

　　基本型需求在金字塔的底层，是必需有的要素，一旦缺失用户就使用不了产品，金字塔就不能平稳矗立，是最重要的。期望型需求是指用户希望能有的需求，此类需求的满足程度与顾客满意度是线性相关的，满足的越多顾客就越满意。兴奋型需求是超出用户预期的需求，此类需求可以极大地提高顾客的满意度，满足此类需求可以给产品加分，不满足也无大碍，其需求的重要程度远低于期望型需求。但是随着市场和时间的变化，对于用户来讲，需求的层次也是一种动态变化的过程，需要及时作出相应的调整。

　　基于上述原则，实际开发过程中要全力以赴地满足顾客的基本需求。然后，尽量满足顾客的期望型需求，提供客户最喜欢的额外服务或功能，使其产品既优于竞争对手又有差异。尽最大能力满足用户的兴奋型需求，为公司创建忠诚度较高的用户群。

　　这种方法的缺点是不够精确，受限于项目干系人各自所负责的模块的侧重点不同等客观因素。要求每个人在每种类别的含义理解上达成一致较为困难，无法按照上述原则对需求确定优先级。此方法只适用于小规模的项目。对于大规模复杂的系统，则需要一种结构化的方法来定量确定优先级。

3 基于AHP的需求优先级排序

　　目前涉及需求排序的算法很少提及层次性，将层次性引入需求排序，AHP（Analytical Hierarchy Process）是美国著名运筹学家SATTYA.L在上世纪70年代提出的[7]。把复杂系统进行层次化，将定性和定量的因素有效地结合起来，通过建立矩阵，排序计算后得出的结果具有较强说服力，与前种方法对比，具有明显的优越性。AHP法可以将一些主观因素以量化的形式表达出来，可以避免人的主观性因素与计算出的结果相矛盾，使得用户的需求更加清晰和条理化，让决策更加有效。AHP方法大致可以归纳为以下几步[8]：（1）分析各个关键因素之间的联系，创建清晰的递阶层次结构；（2）两两比较同一层次较上一层次中某个准则的重要程度，建立矩阵；（3）通过矩阵计算各元素之间的相对权重；（4）计算每个元素相对于整体目标的合成权重，得到先后次序。

　　3.1 层次结构模型建立

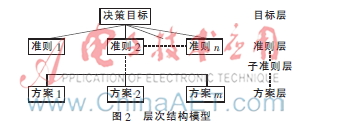
　　AHP算法中很重要的步骤是将顾客的需求进行分解，建立递阶层次结构。根据属性的差别，这些元素被分为几个组，构成不同层次，然后作为准则，支配下一层的元素，而它也支配上层元素，这些被分解的要素从上到下形成一个递阶层次。最上面的被称为目标层，即理想结果或预定目标；中间层包含了为到达最上层目标所要考虑的中间环节，由几个层次构成，一般为准则或子准则；最下面一层是采取的方案等。如图2所示。

　　3.2 确定相对重要性矩阵并计算各自权重

　　相对彼此的重要性建立起准则的矩阵，两两比较各个准则，得到每个评价准则之间的相对重要性。如果比较矩阵记作E，E=（eij），矩阵E中的元素eij反映元素Ei相对于Ej的重要程度。矩阵E是一个互反矩阵，eij（其中i=1，2，…，n；j=1，2，…，n）有如下性质：eij>0，eij=1（当i=j），eij×eji=1（当i≠j）。一般采用9级标度法确定矩阵元素eij的数值，即eij的取值范围是1，2，…，9，其互反数的取值范围是1，1/2，…，1/9。在9级标度法中eij值与被比较元素的相对重要程度之间的对应关系如下：

　　（1）Ei与Ej同等重要，则有eij=1，eji=1；

　　（2）Ei比Ej略微重要，则有eij=3，eji=1/3；

　　（3）Ei比Ej明显重要，则有eij=5，eji=1/5；

　　（4）Ei比Ej十分重要，则有eij=7，eji=1/7；

　　（5）Ei比Ej极其重要，则有eij=9，eji=1/9。

　　如果两个对比元素之间的相对重要性在上述判断之间，eij可以取2、4、6或8。对于权重的计算可以用特征根法，对于每个矩阵E，能够对应一个特征方程EW=λmaxW，求解特征方程的最大特征根λmax和对应的特征向量W，然后将特征向量W归一化后就可作为权重向量。WE即为权向量。

　　为了避免出现A比B重要、B比C重要、而C又比A重要这种循环情况，需要进行一致性指标计算YC.I[9]（Consistency Index）：

　　YC.I=（λmax-n）/（n-1）

　　根据表1，查找相应的平均随机一致性指标YR.I。

　　计算一致性比例：YC.R=YC.I/YR.I，只有当YC.R<0.1时通过一致性检验。

　　将通过检验的权重比较后根据WE顺序排列，需求优先级即量化地展示在开发者面前。

　　3.3 应用举例

　　本文结合青岛某船厂信息管理系统来验证该AHP方法确定需求优先级算法的可行性。因项目时间和人员等客观因素，无法短时间内全部满足，利用AHP方法计算出各个模块的优先级，分步完成该系统。该信息化系统主要包含以下几个需求：（A）财务管理，包括付款管理、财务审核、账务管理等；（B）人力资源管理，包括员工管理、薪资管理、社保管理、培训管理等；（C）采购管理，包括物料管理、备件管理等；（D）基础信息管理，包括船舶基础信息管理、物料基础信息管理、供应商基础信息管理等；（E）报表管理，包括各类详细数据的查询、计算、导出和预估；（F）后台管理，包括用户角色管理、权限管理、系统设置等。

　　根据以上需求[10]首先建立层次结构模型。目标层，就是完成一个功能完善的管理系统；准则层，将价值V，费用C，风险R这三项作为评价指标；方案层，就是需求分析出来的各个功能单元。通过两两比较的方法导出低阶层次结构模型中各层次元素的权重，得到各种需求的优先级。从用户那里得到针对某层中的两个元素，对于上层元素哪个更重要，按1~9的比例赋值。两两比较判断矩阵。准则层判断矩阵：

　　根据上述方法进行一致性检验。计算得出：YC.R=YC.I/YR.I=0.003 7/（2×0.58）=0.003<0.1，通过一致性检验。

　　构造方案层中相对于三个准则的判断矩阵并计算出相应权向量，如表2~表4所示。

　　YC.R=0.036<0.1，通过一致性检验。

　　YC.R=0.091<0.1，通过一致性检验。

　　YC.R=0.046<0.1，通过一致性检验。

　　由上面三个矩阵的特征向量WV，Wc，Wr以及WE可以得到6种需求的权重：

　　W=（WV，Wc，Wr）WE

　　=（0.132 5，0.202 4，0.103 0 ，0.148 8，0.073 5，

　　0.339 8）T

　　6种需求的顺序通过公式计算出来，即：采购管理>报表管理>财务管理>人力资源管理>基础信息管理>后台管理。该项目的前期需求确定及后期的开发中，由于正确规划了项目的需求优先级顺序，在人力和时间都很紧张的情况下，还是按照客户要求交付了项目，这都取决于前期需求的准确获取及与客户的充分沟通，以及运用科学的方法，否则项目很容易失败。

　　3.4 AHP改进算法

　　使用AHP也有它的局限性。假如把全部需求不经任何甄别都放在同一层上进行权重比较，显然是不合适的。如果这种需求过多，使用该方法会非常糟糕。如果有21个需求需要在同一层次比较，用户要进行210次的两两比较，这样很容易出现错误和不一致。所以在排序需求优先级时，考虑将需求分层是十分重要的。这时可以引入解释结构模型技术（ISM）。ISM用于明确问题的层次和结构，将系统的要素分在不同的层次上，避免过多的要素出现在同一层次上。其原理就是抽取问题的组成要素，利用有向图、矩阵等工具，对要素及相互关系进行处理，明确问题的层次和整理结构。将大量需求进行分层后就可以继续使用AHP进行需求优先级排序。

　　3.5 其他影响因子

　　通常需求优先级排序方法都是基于功能和价值来进行考虑的，不可否认需求的价值是优先级排序的重要依据，但是，需求优先级排序不应只考虑它的效益型属性，还应考虑它的成本型属性，包括开发时间、成本和风险等。下面简要介绍如何量化这些因素。

　　（1）时间，主要是根据程序开发、测试等人员对提交的工作完成时间的承诺，考虑开发的复杂性，结合历史相似规模项目经验综合考虑各需求所需时间。

　　（2）开发成本，运用E=A×sizeB×M来计算。E为工作量，A是一个常数，反应实际开发软件类型，Size为估算的代码行数，B反映与工作量不成比例的因素，一般取1~1.5，M反映了不同过程及开发特征的混合因素，如产品复杂性、可靠性等。

　　（3）风险，引用一个风险影响水平定义[11]：RE=P×C，其中P是风险发生的可能性，C是风险会带来的损失。从需求的变动、沟通的障碍、是否准确估算系统规模、软件的有效使用周期等几种风险分别估算P值和C值，按照RE=P×C来计算RE。

　　综合考虑了需求的成本型属性和效益型属性后，可以定义各个属性因素所占的权重，最后可以得出更加全面的需求优先级排序。

4 结束语

　　需求优先级的确定是软件开发中的一个较为重要的基本问题，本文依据软件规模的大小，确定需求优先级排序的最优方法，并综合项目的多重属性进而求得最准确的排序结果，解决了在需求优先级排序过程中千篇一律地套用某一种方法，从而使效率低下，而且结果有偏差的问题。需求优先级确定过程中要充分依靠需求调查的原始资料，这样确定的需求才能更加符合顾客要求，做出的软件产品更加让顾客满意。

参考文献

　　[1] WIEGERS K E. Software requirements[M]. [S.l.] Microsoft Press， 2003.

　　[2] 吴海静.IT企业敏捷开发中基于优先级的需求管理[D].上海：复旦大学，2012.

　　[3] 王越，刘春，张伟，等.知识引导的软件可信性需求的提取[J].计算机学报，2011，34（11）：2166-2174.

　　[4] 孙莉.软件项目管理中的需求管理[J].信息系统工程，2011（4）：58-59.

　　[5] 李华莹，胡兢玉.回归测试用例优先级排序技术研究[J].计算机仿真，2013，30（10）：298-301.

　　[6] KARLSSON J， WOHLIN C， REGNELL B. An evaluation of meth-ods for prioritizing software requirements[J]. Informationand Software Technology，1998，39（14-15）：938-947.

　　[7] 王莲芬，许树柏.层次分析引论[M].北京：中国人民大学出版社，1989.

　　[8] 湛浩旻，印桂生，王红滨.基于解释结构模型的需求最高优先级设定方法[J].计算机应用研究，2012，29（11）：4191-4192.

　　[9] 王玉英，陈平，苏旸.生成有向图中全部简单回路的一种有效算法[J].计算机应用与软件，2009，26（12）：27-29.

　　[10] 杨广华，包阳，李东红，等.基于需求的测试用例优先级排序[J].计算机工程与设计，2011，32（8）：2724-2727.

　　[11] 李厚明.软件项目需求变更风险管理[D].济南：山东大学，2012.