摘 要: 在双目立体视觉系统中,图像匹配是关键步骤之一。在众多匹配算法中,归一化互相关(NCC)算法由于具有精度高、鲁棒性强等优点得到广泛应用,但其计算量大、运算速度较慢,使其难以在线应用。为此,本文提出一种改进的NCC立体匹配算法,通过引入积分图像和平方积分图像,将矩形窗口区域像素求和运算转化为四个像素点值的简单相加减,同时剔除基准图像中无法匹配区域以减小搜索范围,使计算复杂度得到简化,计算量大为降低。实验证明,改进后的NCC算法在保证匹配质量的基础上,执行速度得到显著提高,利于在线应用。
关键词: 图像匹配;归一化互相关(NCC); 积分图像 ; 图像处理
0 引言
双目立体视觉是计算机视觉的一个重要分支,近年来,双目立体视觉技术得到了大量研究[1],主要应用在机器人导航、三维测量和虚拟现实等领域。双目立体视觉系统的实现过程由图像获取、摄像机标定、特征点提取、图像匹配和三维立体重建等步骤组成[2]。图像匹配本质上是寻找两幅图像的相似性[3-4],是恢复三维立体场景的先决条件[5],是立体视觉系统中的关键技术之一。双目立体视觉图像匹配[6]技术是通过两台水平摆放的摄像机分别获取两幅图像,并从中找出相同景物各像素点的对应关系,得到其最佳视差值,最终获得图像视差图的技术。
图像匹配方法按照匹配基元不同可分为特征匹配[7]、相位匹配[8]和区域匹配[1,9]三种。特征匹配是针对提取的特征进行描述,然后运用所描述的参数进行匹配的一类算法,计算量小,速度快,但是匹配效果受到图像特征稀疏性的影响难以获得致密视差图。相位匹配是最近才发展起来的一类算法,能够反映信号的结构信息和抑制图像的高频噪声,适用于并行处理存在相位奇点和相位卷绕问题的情况。区域匹配是基于局部窗口间灰度信息相关程度的匹配算法,常用的匹配相似度量函数有NCC(Normalized Cross Correlation,归一化互相关)、SAD(Sum of Absolute Differences,差绝对值和)和SSD(Sum of Squared Differences,差平方和)。这三种算法中,NCC算法最常用,它通过计算视差范围内基准图像与实时图像对应像素点间的相关性来获取视差图,相关系数一般在[-1,1]之间取值,该算法将搜索相关系数最大值对应的视差作为最佳视差值,具有精度高、鲁棒性强[10]的优点,缺点是计算量大、速度慢,在线应用受到限制。
本文针对NCC算法的缺点,通过在立体匹配中引入积分图像和平方积分图像,并且剔除基准图像中无法匹配区域,对原NCC算法进行了改进,在保证匹配质量的情况下,使匹配速度得到显著提高,实验结果验证了该改进算法的有效性和快速性[11]。
1 积分图像及平方积分图像
1.1 积分图像
积分图像(Integral Image)理论是Viola P.等于2001年提出的[12]。积分图像是一种用于快速计算图像某窗口区域灰度和的一种图像中间表示,有较广泛的应用[13-15]。积分图像中任意一点(i,j)的值用ii(i,j)表示,代表了源图像中行数小于i、列数小于j的所有灰度值的和,即:

其中i(x,y)表示源图像中(x,y)点的灰度值。令s(i,j)为源图像中第i行、第j列的灰度值积分,则有:
s(i,j)=s(i,j-1)+i(i,j)(2)
ii(i,j)=ii(i-1,j)+s(i,j)(3)
利用式(2)和式(3)编程实现时,应该扩展一行一列以确保i-1,j-1为正数。
如果要计算原始图像中顶点依次为A、B、C、D的矩形窗口,只需将原图像遍历一遍得到积分图像后,利用四个顶点对应的值进行简单加减运算,即可求得该区域灰度。不管矩形窗口区域有多大,利用积分图像只需进行3次加减运算,即:
S=p(D)+p(A)-p(B)-p(C)(4)
其中,S表示矩形窗口区域的灰度值;p(A)、p(B)、p(C)和p(D)分别表示矩形顶点的灰度值。
1.2 平方积分图像
为了能够快速获得区域内像素点灰度平方和,在积分图像基础上引入了平方积分图像[15],在实际应用中以矩阵形式存储,平方积分图像中任意一点值表示为Pii(i,j),即:

其中i2(x,y)表示源图像中(x,y)点的灰度值的平方,参考式(2)、式(3),源图像中第i行、第j列的灰度平方积分Ps(i,j)以及平方积分图像中任意一点(i,j)的值 Pii(i,j)可以分别由下面公式求得:
Ps(i,j)=Ps(i,j-1)+i2(i,j)(6)
Pii(i,j)=Pii(i-1,j)+Ps(i,j)(7)
再利用式(4),可求出某窗口区域的灰度值平方和,运算简单,计算量大幅降低。
2 NCC算法及其改进
2.1 原NCC匹配算法
图像匹配本质上是求两图像间的相似性,即针对右图待匹配点,在视差d所有可能取值范围[0,disMax]内,计算(disMax+1)个归一化系数,取相关系数最大值对应的左图点作为最佳匹配点,对应的d为最佳视差。若选择图像尺寸为M×N,模板窗口尺寸为m×m,则归一化互相关系数计算式如下[16]:
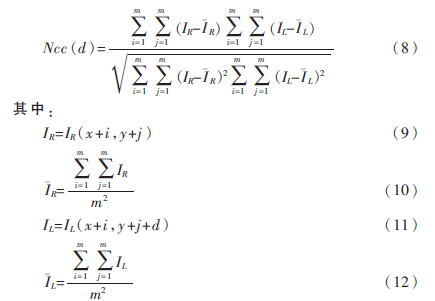
由式(8)可知,对于每一视差,在计算相关性系数时都需要对窗口区域求均值,复杂度较高,消耗的时间长,所以实时性差。
2.2 改进的NCC算法
在原NCC算法中涉及到求窗口区域像素的均值,因此在计算每一个视差值时都要进行6(m×m-1)次加法、4(m×m-1)次减法、2(m×m-1)次乘方、2次乘法、3次除法和1次开方,而且计算的次数随着窗口m×m大小的变化而变化,模板窗口越大,匹配时消耗的时间越多。为了减低计算量,对归一化互相关系数先不进行求均值运算,而是将其分子分母先展开化简。基于此,对归一化互相关系数进行重推可得:
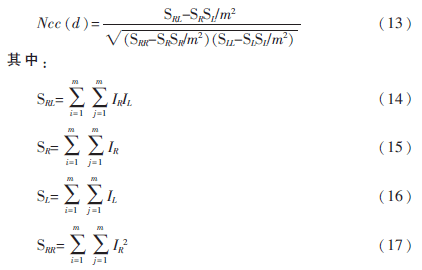
其中:

其中,式(14)利用卷积运算降低计算复杂度,而式(15)~(18)均可以用积分图像或平方积分图像计算窗口区域的值,因此区域灰度值的和可用四个顶点简单的加减运算来代替。基于上述分析,对于每一个视差值只需要进行8次加法、7次减法、4次除法、4次乘法、1次开方和1次卷积,而且在计算量上不会随模板窗口大小变化而变化,这极大地降低了计算相关系数过程中的难度。从计算量上引入积分图像后有利于降低复杂度,提高运算速度。
由于双目立体匹配中两图像间存在视差,右图右边界的许多点在左图上找不到相匹配的点并且模板窗口有一定的尺寸,由此其实际匹配的区域范围是y≤N-dispMax+m,x≤M-m。剔除掉无法匹配的区域既能确保匹配点完全被搜索到,又可以减少匹配时间、提高搜索效率。
图像匹配是三维重建的一个重要步骤,而在获得图像时物体的几何信息会丢失,因此匹配时需要遵循多个约束条件[17]才能保证重建过程的正常进行,包括:
(1)外极线约束;
(2)唯一性约束,指右图中某点与左图的对应点是确定且唯一的,它们的关系与一次函数中自变量和应变量的关系是一样的,不存在一对多的形式;
(3)连续性约束;
(4)视差有限性约束,认为在匹配时两图像间的视差是有界的;
(5)左右一致性约束,指不管选择左图或右图作为基准图,它们之间的对应关系是不变的。
通过前面分析,对NCC算法进行改进,引入积分图像和平方积分图像后,其实现步骤如下:
输入:右摄像机采集的基准图像IR,左摄像机采集的实时图像IL。
输出:视差矩阵,显示视差图。
步骤1:计算IR和IL对应的积分图像和平方积分图像,用SR、SRR和SL、SLL表示,并且对x、y赋初值。
步骤2:在视差范围内,利用式(4)对积分图像和平方积分图像进行简单的加减运算,求取模板窗口和搜索窗口覆盖区域灰度值的和及其灰度值的平方和。
步骤3:利用矩阵卷积,计算模板窗口与搜索窗口所包含区域的SRL。
步骤4:利用式(13)计算相关系数,重复步骤2~3,直到满足y≤N-dispMax+m且x≤M-m条件时,获得最佳匹配的视差矩阵,返回视差图。算法流程图如图1所示。

3 实验验证与分析
本文实验采用CPU为Pentium(R)Dual-Core、内存为1.96 GHz的PC机,采用的编程环境为MATLAB 2011b。
3.1 标准测试图像验证与分析

文中采用两组国际通用标准测试图进行实验。图2为测试图Teddy;图3为测试图Cones;图4为两组测试图的标准视差图;图5是利用NCC算法获得的视差图;图6是本文提出的改进NCC算法获得的视差图。
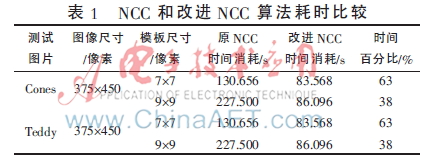
由图5可以看出在右边界区域不存在匹配点,利用NCC算法在此区域进行匹配会增加计算时间,影响实时性;图6的改进NCC算法在匹配时剔除了无法匹配的区域,提高了算法的计算效率。表1给出了当模板尺寸为m=7像素和m=9像素时的时间消耗,从中可以看出,改进的NCC算法比原算法耗时大为减少,提高了算法的实时性。当m=9像素时消耗的时间仅为原算法的38%,并且时间消耗几乎不受模板尺寸的影响。同时,将两种算法得到的视差图与标准视差图进行比较发现,改进NCC算法具有更好的精度和鲁棒性。
3.2 实际采集图像验证与分析
本实验采用Point Grey公司生产的Bumblebee2型号立体摄像机对场景进行采集,得到校正后的图像见图7,选择右摄像机拍摄的图像为基准图像、左摄像机拍摄的图像为实时图像。图8为利用NCC算法和本文算法得到的视差图。


表2给出了两种算法的耗时情况,从中可以看出,改进NCC算法减少时间消耗显著。比较表1和表2数据,当图像尺寸和模板尺寸越大时,改进的NCC算法越能够表现其优越性。
4 结束语
本文通过引入积分图像和平方积分图像,并剔除源图像中无法匹配区域,改进了原NCC算法,降低了计算复杂度,提高了匹配速度。当图像尺寸和模板窗口越大、左右图像视差越大时,耗时减少更为显著,且保持了较好的匹配精度,如果利用VC等高级语言移植到机器人等环境建模,可以进行在线立体匹配。
参考文献
[1] 隋婧,金伟其.双目立体视觉技术的实现及其进展[J].电子技术应用,2004,30(10):3-7.
[2] 程黄金.双目立体视觉系统的技术分析与应用前景[J].电脑知识与技术,2011,7(9):2145-2147.
[3] 孙卜郊,周东华.基于NCC的快速匹配算法[J].传感器与微系统,2007,26(9):104-106.
[4] ZITOVA B, FLUSSER J. Image registration methods: a survey[J]. Image and Vision Computing, 2003,21(11): 977-1000.
[5] 贾贝贝,阮秋琦.双目立体视觉的三维人脸重建方法[J].智能系统学报,2009,4(6):513-520.
[6] 钱曾波,邱振戈,张永强.计算机立体视觉研究的进展[J].测绘学院学报,2001,18(4):267-272.
[7] 曾峦,王元钦,谭久彬.改进的SIFT特征提取和匹配算法[J].光学精密工程,2011,19(6):1391-1397.
[8] 林静,江开勇,林俊义,等.基于立体校正的快速相位立体匹配[J].贵州师范大学学报(自然科学版),2013,31(2):92-95.
[9] 白明,庄严,王伟.双目立体匹配算法的研究与进展[J].控制与决策,2008,23(7):721-729.
[10] WEI S, LAI S. Fast template matching based on normalized cross correlation with adaptive multilevel winner update[J]. IEEE Transactions on Image Processing, 2008,17(11): 2227-2235.
[11] 徐奕,周军.立体视觉匹配技术[J].计算机工程与应用,2003,15(5):58-62.
[12] VIOLA P, JONES M. Rapid object detection using a boosted cascade of simple features[C]. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2001:511-518.
[13] PORIKLI F. Integral histogram: a fast way to extract histograms in cartesian spaces [C]. Proceedings 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition,2005:829-837.
[14] LAMPERT C, BLASCHKO M, HOFMANN T. Efficient sub-window search: a branch and bound framework for object localization[J]. Pattern Analysis and Machine Intelligence, 2009,31(12):2129-2142.
[15] 邵平,杨路明.基于模板分解和积分图像的快速Kirsch边缘检测[J].自动化学报,2007,33(8):795-800.
[16] 韩冰,王永明,刘杨,等.一种基于积分图像的快速归一化积相关算法[J].弹箭与制导学报,2009,29(5):283-286.
[17] 肖艳青,刘党辉,孙朋.图像立体匹配研究进展[J].测控技术,2009,28(8):1-5.

