摘  要： 增量式数字PID是自动控制系统优化过程中应用广泛的一种控制方法。分析了增量式PID参数调节对控制器性能以及系统环路性能的影响。MATLAB频域仿真结果表明，Kp、Kd、Ki值的改变直接造成PID控制器零点的位置发生移动，从而使得控制系统动态性能得到改善。

　　关键词： 增量式数字PID；参数调节；频域分析

0 引言

　　计算机控制系统的核心是数字调节器，工程中常用的数字调节器控制方法有以下几种：（1）直接数字控制：根据采样理论和离散化后的数字模型设计数字控制器，该方法的前提是得到系统的数字模型；（2）比例-积分-微分（propotional-integral-derivative，PID）控制：调节器的输出是其输入的比例、积分和微分的函数，特点是不需要被控对象的数字模型，结构简单、稳定可靠，故工程应用广泛；（3）最优控制：基于性能指标J最小的控制策略（燃料最省、路径最短、时间最短），依赖于对象的数字模型；（4）智能控制：包括神经网络、模糊控制等，基于仿人类思维的模糊数据推理方法，不需要数字模型，但控制算法复杂。

1 增量式PID算法的数字实现

　　数字PID控制系统是时间的离散系统，Proportional（比例）、Integral（积分）、Differential（微分）可根据系统的要求，对输入的偏差按比例、积分和微分的函数关系运算得到控制量，输出到执行器完成相应的调节任务[1]。在PID调节中，由于PID算式可以灵活地改变其结构，因此选择不同的P、I、D会得到不同的控制效果，特别是当算法中某些参数选择不当时，会引起控制系统的超调或振荡，这对某些生产过程是十分有害的[2]。为了避免这种有害现象的发生，分析和研究PID算法，确定合理的PID参数是必要的，同时对PID控制技术的广泛应用具有重要的意义。

　　PID算法的模拟表达式如式（1）所示：

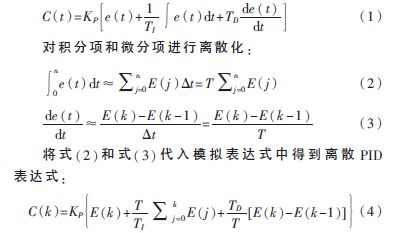
　　上式的输出与系统位置一一对应，也称为位置型PID算式。用位置型PID算式计算C（K），需要用到各采样时刻的偏差值，计算复杂，且需要占用内存。

　　对于系统（k-1）时刻的输出：

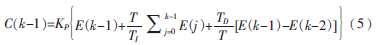
　　将式（4）、式（5）相减后得到如下表达式：

　　C（k）-C（k-1）=KP[E（k）-E（k-1）]+KIE（k）+

　　KD[E（k）-2E（k-1）+E（k-2）]（6）

　　式（6）表示第k次输出的信号增量，称为增量型PID控制算式。

　　位置型算式不仅需要对E（j）进行累加，而且计算机的任何故障都将引起C（k）的大幅度变化，对生产不利。增量型较位置型的优点如下：（1）由于输出的是增量，所以误动作小；（2）易于实现手动/自动的无扰切换（位置型算法中，当由手动切换到自动时，首先需要保证控制器的输出等于实际的控制量；增量型算式只给出偏差，而与原来位置无关）；（3）不产生积分失控，容易获得良好的调节品质。

2 增量型PID参数调节对控制器的性能影响

　　对于增量型PID数字控制策略，为了便于分析其对系统性能的影响，将差分方程进行Z变换得到脉冲函数，如式7所示：

　　从校正系统的传递函数中可以简单地看出Kp、KI、KD、T均与控制器的零点相关。

　　2.1 Kp变化对幅值相位的影响分析

　　根据增量式PID的传递函数编写MATLAB命令如下：

　　kp=0.002*32*1023/3.3*2.49/10.36/3300；

　　ki=0.002*32*1023/3.3*2.49/10.36/3300；

　　kd=0.002*32*1023/3.3*2.49/10.36/3300；

　　fs=（150e3）；

　　a=tf（[kd/fs kp ki*fs]，[10]）；

　　a1=tf（[kd/fs kp*100 ki*fs]，[1 0]）；

　　a2=tf（[kd/fs kp/100 ki*fs]，[1 0]）；

　　bode（a，′-′，a1，′--′，a2，′.-′）；

　　a中Kp采用标准值，a1中Kp值增大为a中Kp值的100倍，a2中Kp值减小为a中Kp值的百分之一。MATLAB仿真画出PID校正装置相应的Bode图，如图1所示。

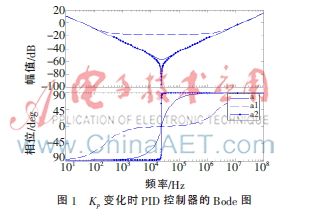
　　从图1可以明显看出，随着Kp增大，PID控制器两个零点逐渐分离，且起始增益无明显变化；反之，Kp减小，两个零点向中间靠拢。

　　2.2 KI变化对幅值相位的影响分析

　　MATLAB仿真时，a采用KI标准值，a1中KI值增大为a中KI值的100倍，a2中KI值减小为a中KI值的百分之一，相应的Bode图如图2所示。

　　从图2可以明显看出随着KI增大（a2→a→a1），零极点右移，左边零点右移，最终两个零点同时右移，起始增益明显增加；反之，KI减小（a1→a→a2），零极点左移，左边零点左移，起始增益明显减小。

　　2.3 KD变化对幅值相位的影响分析

　　MATLAB仿真时，a采用KD标准值，a1中KD值增大为a中KD值的100倍，a2中KD值减小为a中KD值的百分之一，相应的Bode图如图3所示。

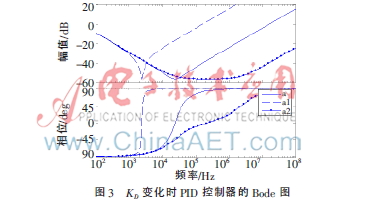
　　从图3可以明显看出，随着KD增大（a2→a→a1），右边零点左移，最终两个零点同时左移，起始增益无明显变化；反之，KD减小（a1→a→a2），右边零点右移。

3 PID参数调节对系统稳定性能的影响分析

　　为了进一步分析PID参数调节对系统性能的影响，本文以Buck变换器在电阻性负载下的传递函数模型为例进行说明。

　　3.1 Buck变换器的小信号模型

　　Buck变换器闭环控制系统如图4所示。

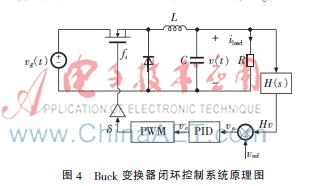
　　Buck变换器工作在连续电流模式（CCM）下，其小信号传递函数如式（10）所示：

　　3.2 Kp变化对系统性能的影响分析

　　带PID控制器的Buck变换器系统的开环传递函数为：

　　G（s）=GC（s）Gvd（s）

　　MATLAB仿真时，Buck变换器取如下参数：Vg=50/4 V，L=0.24 H，RDCR=0.7 Ω，C=330 F，RESR=0.1 mΩ，R=10 Ω；G采用Kp标准值，G1中Kp值增大为G中Kp值的10倍，G2中Kp值减小为G中Kp值的十分之一，仿真得到系统的Bode图如图5所示。

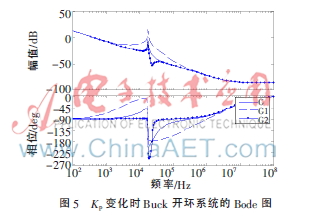
　　从图中可以明显看出，随着Kp减小（G1→G→G2），系统谐振峰值减小，有利于系统的平稳性，但系统相位裕量会减小甚至出现负值，从而导致系统不稳定。

　　3.3 KI变化对系统稳定性能的影响分析

　　G采用KI标准值，G1中KI值增大为G中KI值的10倍，G2中KI值减小为G中KI值的十分之一，仿真得到系统的Bode图如图6所示。

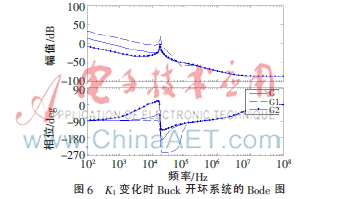
　　从图中可以明显看出随着KI增大（G2→G→G1），系统相位裕量明显减小，并出现负值，导致系统不稳定，故在PID设计中KI系数虽然有利于消除静差，但仍不能取值太大。

　　3.4 KD变化对系统稳定性能的影响分析

　　G采用KD标准值，G1中KD值增大为G中KD值的10倍，G2中KD值减小为G中KD值的十分之一，仿真得到系统的Bode图如图7所示。

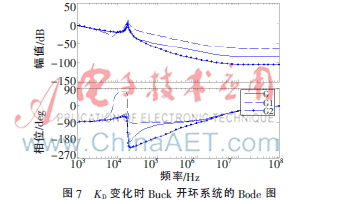
　　从图中可以明显看出，随着KD减小（G1→G→G2），系统抗噪声能力增强，但相位裕量会出现负值，从而导致系统不稳定。

4 结论

　　通过以上对数字增量式PID控制算法的分析与研究，可得出PID参数调节对控制器本身性能的影响如下：

　　（1）Kp对增益影响不大，且Kp的增大导致两个零点频率分离。

　　（2）KI对低端增益有影响操控，因为KI增大，零极点频率增大。同时，KI增大，左边的零点右移，当左边的零点达到右边零点频率时，两个零点同时右移。

　　（3）KD对增益影响不大，且KD的增大导致右边零点左移，当右边的零点达到左边零点频率时，两个零点同时左移。

　　在对系统进行增量式数字PID校正过程中，系统的稳定性、快速性、平稳性以及准确性是相互矛盾、不能同时兼得的，故应根据实际情况合理选择Kp、KI、KD参数优化系统性能。尤其当Kp、KD变小或KI值增大时，系统相位裕量会出现负值，从而导致系统不稳定，在实际设计中应注意避免。

参考文献

　　[1] 胡寿松．自动控制原理[M]．北京：科学出版社，2013．

　　[2] 刘光亚，彭维娜．PID参数性能分析及改进[J]．湖北工业大学学报，2013，28（1）：60-63．

　　[3] ERICKSON R W， MAKSIMOVIC D． Fundamentals of Power Electronics[M]． USA：Kluwer Academic Publishers，2001.