文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.12.024
中文引用格式: 袁全盛,胡永江,王长龙. 无人机通信中的非对称物理层网络编码研究[J].电子技术应用,2015,41(12):90-93.
英文引用格式: Yuan Quansheng,Hu Yongjiang,Wang Changlong. Asymmetric physical-layer network coding over UAV communication[J].Application of Electronic Technique,2015,41(12):90-93.
0 引言
无人机(Unmanned Aerial Vehicle,UAV)在通信、侦察、搜索、监测以及实时打击等方面有着越来越多的应用,在未来战场中将扮演重要的角色[1-2]。随着无人机技术的发展,无人机的飞行高度、续航时间以及负荷能力有了很大的提高,同时,无人机机动性好、成本较低的特点使得无人机组网通信具有方式灵活、易于部署以及设备更新方便的优势,因此无人机作为中继平台具有现实意义和很大的优势[3]。在无人机组网通信中,任务无人机和中继无人机之间的信道以及中继无人机和地面控制终端之间的信道存在明显差异[4]。因此,将地面终端-中继无人机-任务无人机构成的无线中继链路建模为非对称双向中继信道(Two Way Relay Channel,TWRC)模型是符合实际应用环境的。
物理层网络编码(Physical-layer Network Coding,PNC)可以提高通信系统的网络吞吐量[5]。将物理层网络编码应用到无人机组网通信中,对于提高无人机通信系统的实时性具有重大意义。然而,要将物理层网络编码应用到无人机通信系统中,需要考虑非对称条件下的物理层网络编码。文献[6]提出基于重复累计(RA)编码的非对称速率协同分集网络编码方案,保证了较差链路传输的可靠性和较优链路传输的高效率,该方案进行一次信号传输需要3时隙。为提高吞吐量,文献[7]提出了两种2时隙的TWRC不对称物理层网络编码传输方案。第一种方案采用级联信道编码,调制时两个端节点仍然采用相同的调制方式,系统的复杂度较低;第二种方案采用子集编码和子集调制,采用该方案时两个端节点的调制和解调方式需作出相应的改变,复杂度较高,但性能较好。文献[8]对非对称调制物理层网络编码方案进行了研究,提出了基于符号映射的物理层网络编码方案,分析了BPSK-QPSK模式的非对称调制方案的性能。
文献[7]中第二种方案使用的是卷积码,如果使用纠错能力更强的信道编码,如低密度奇偶校验(Low Density Parity-Check,LDPC)码,可以进一步提高系统的可靠性。从上面提到的文献中可以看出,如何基于2时隙的传输模型,将物理层网络编码、信道编码以及非对称调制三者联合设计,提出一种适应多种调制方式的方案,仍是一项具有挑战性的工作。
为进一步提高系统的可靠性,研究不同非对称调制模式的性能,本文针对无人机组网通信的实际环境,建立非对称双向中继信道模型,提出了无人机通信中基于LDPC码的非对称调制物理层网络编码方案,即非对称多阶相移键控物理层网络编码方案(Asymmetric M-ary phase-shift keying Physical-layer Network Coding,AMPNC)。本文分析了AMPNC的性能,进一步改善了系统的中断性能等指标,更加符合无人机组网通信的实际环境,为物理层网络编码在无人机通信中的应用提供了理论依据。
1 系统模型
非对称条件下的物理层网络编码可以分为四种:相位非对称、上行链路非对称、下行链路非对称、节点非对称[9]。因为非对称调制发生在节点中,因此本文的研究主要基于节点非对称的情形。基于无人机组网通信的实际应用环境以及双向中继信道模型[10],建立非对称双向中继信道模型。如图1所示,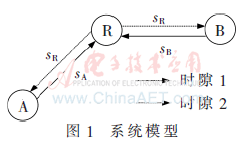 节点A为地面终端,节点R为中继无人机,节点B为任务无人机。为提高遥控信号的抗干扰能力和遥测信号的传输速率,在节点A和节点B采取不同的调制方式,其中,节点A的调制方式为低阶调制,节点B的调制方式为高阶调制。香农分离定理表明,对确定的系统,独立设计信源和信道编码不会对最优性能带来损失。根据该定理,本文不考虑具体的信源编码方式。
节点A为地面终端,节点R为中继无人机,节点B为任务无人机。为提高遥控信号的抗干扰能力和遥测信号的传输速率,在节点A和节点B采取不同的调制方式,其中,节点A的调制方式为低阶调制,节点B的调制方式为高阶调制。香农分离定理表明,对确定的系统,独立设计信源和信道编码不会对最优性能带来损失。根据该定理,本文不考虑具体的信源编码方式。
2 非对称传输方案
基于无人机组网通信的实际环境,对非对称条件下的物理层网络编码进行研究,提出物理层网络编码、信道编码和非对称调制三者结合的信号传输方案。不失一般性,为了方便阐述AMPNC方案,假设节点A的调制方式为QPSK,节点B的调制方式为8PSK。对于其他的非对称MPSK调制方式,可采用类似的方法对方案进行阐述。
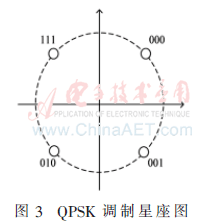
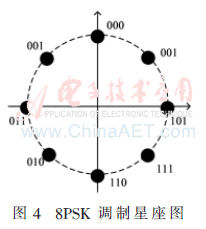
如图2所示,在多址接入阶段,节点A首先将未编码信息xA进行LDPC编码,编码后的信息为cA,将cA进行QPSK调制(调制星座图如图3所示),调制后的信息为sA,并将sA通过节点A到节点R之间链路发送到中继。在节点B,首先将未编码信息xB进行LDPC编码,编码后的信息为cB,将cB进行8PSK调制(调制星座图如图4所示),调制后的信息为sB,并将sB通过节点B到节点R之间链路发送到中继。假设节点A到节点R之间的信道参数为hAR,节点B到节点R之间的信道参数为hBR。
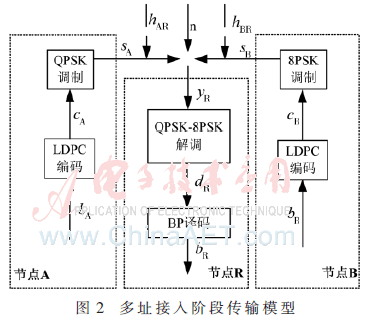
节点R接收到的叠加和信号可以表示为:

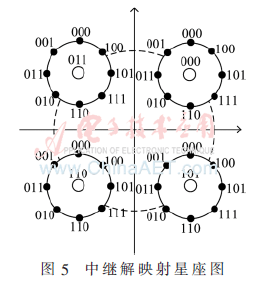
节点R接收到节点A和节点B发送的叠加和信息xR,通过解调得到信息dR(解映射星座图如图5所示),将dR通过BP算法解码后得到解码后信息bR。
3 性能分析
3.1 中断概率分析
从信息论的角度出发,定义中断事件为无法支持在速率R上可靠传输的一组信道事件。在图2中,节点R的信道容量为:

节点R处的中断概率为:

其中,Γ=P/N0,min操作是考虑到系统的性能被节点A到节点R之间的链路和节点R到节点B之间的链路中较差的链路所限制,只有中继译码正确时才能实现准确的转发操作。
因为lb是个单调函数,则中断事件等价于:

在式(7)中,R是链路的传输速率。将各个节点的发射功率以及各条信道的信道衰落的包络代入式(7),可得到节点A到节点B的中断概率。节点B到节点A的中断概率的分析方法与上面类似。
3.2 误码性能分析
首先分析MPSK调制下无线通信系统的误码率表达式:
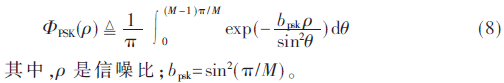
假设节点R能以可接受的误码率解调译码,则以功率PR向节点A和节点B广播信号sR,否则中继无法广播。下面以节点A为例进行分析。中继译码错误的概率为ΦPSK(PA|hAR|2/N0),译码正确的概率为1-ΦPSK(PA|hAR|2/N0)。计算系统的条件BER如下:
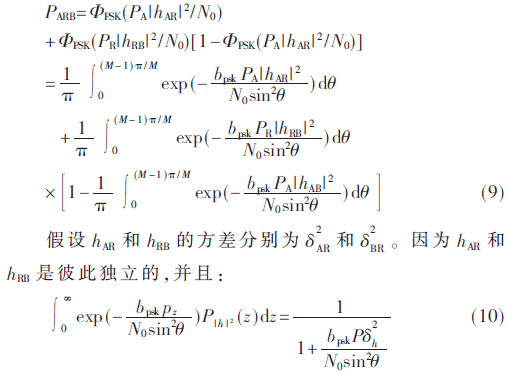
因此,得到图1所示系统的BER如下所示:
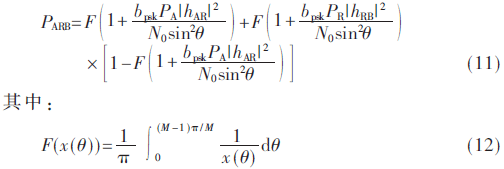
节点B到节点A的链路的BER计算与节点A到节点B类似。
4 实验结果
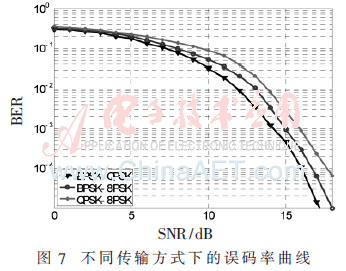
本节在设定的实验条件下,根据所设计的AMPNC方案,进行了仿真实验。图6给出了节点A和节点B发射功率不同时,不同调制方式对中断概率的影响比较图。假设节点A采用MA阶PSK调制方式,节点B采用MB阶PSK调制方式,则节点A的发送功率与节点B的发送功率之比为: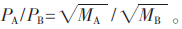 此外,假设无人机组网通信系统的发射功率和恒定,即PA+PB+PR=P,且中继节点的发射功率恒为发射功率和的1/3,即PR=P/3。同时,仿真的其他条件与系统模型设定相同,数据率R=1 b/s/Hz。通过图中比较可以得出,QPSK-8PSK模式的AMPNC方案的中断性能较好,BPSK-QPSK模式的AMPNC方案的中断性能次之,BPSK-8PSK模式的AMPNC方案的中断性能较差。同时,在三种模式中,随着信噪比的增加,系统的中断性能逐渐提高。
此外,假设无人机组网通信系统的发射功率和恒定,即PA+PB+PR=P,且中继节点的发射功率恒为发射功率和的1/3,即PR=P/3。同时,仿真的其他条件与系统模型设定相同,数据率R=1 b/s/Hz。通过图中比较可以得出,QPSK-8PSK模式的AMPNC方案的中断性能较好,BPSK-QPSK模式的AMPNC方案的中断性能次之,BPSK-8PSK模式的AMPNC方案的中断性能较差。同时,在三种模式中,随着信噪比的增加,系统的中断性能逐渐提高。
在图6中,还给出了AMPNC方案与传统传输方案的中断性能的对比。从图中可以看出,在低信噪比时,传统传输方案的中断性能较好;在信噪比约大于10 dB时,AMPNC的中断性能明显优于传统传输方案。
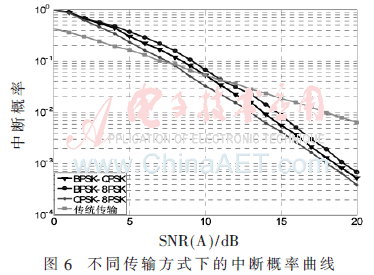
图7给出了节点A和节点B发射功率相同时,不同调制方式对误码率的影响比较图。通过图中可以得出,随着信噪比的增加,系统的误码率逐渐降低。分析图中3条曲线可以得出,BPSK-QPSK模式的AMPNC方案的误码性能最好,这是因为在中继传输过程中,两个可能传输的符号之间的距离主要由中继处的星座距离决定,发送的符号很有可能被误判为该符号在中继节点星座映射图中相邻的符号。在BPSK-QPSK模式中,无论是节点A和节点B的调制星座图,还是节点R的联合解调星座图,其星座距离都是几种模式中最大的,由此造成欧式距离最大,因此该模式的误码性能最好。
5 结束语
本文基于无人机通信的实际环境,建立了无人机组网通信的非对称模型,提出了一种非对称多阶相移键控物理层网络编码方案,研究了非对称衰落信道中不同节点采用不同的PSK调制模式对物理层网络编码性能的影响,在理论分析系统中断性能和误码性能的基础上,对于不同的非对称调制模式对系统中断性能和误码性能的影响进行了实验。仿真结果表明,与传统传输方案相比,AMPNC的中断性能得到很大提高,节点之间发射功率之比对系统的中断性能有很大的影响;BPSK-QPSK模式的AMPNC方案的误码性能最好。在实际应用中,需要根据理论研究成果以及无人机通信对于中断性能、误码性能等具体指标的要求,对系统的调制方案进行设计。本文为物理层网络编码在无人机组网通信中的设计以及性能评估提供了理论依据。
参考文献
[1] SUJIT P B,BEARD R.Multiple UAV exploration of an unknown region[J].Annals of Mathematics and Artificial Intelligence,2008,52(2-4):335-366.
[2] ISCOLD P,PEREIRA G A S,TORRES L A B,et al.Development of a hand-launched small UAV for ground reconnaissance[J].IEEE Transactions on Aerospace and Electronics Systems,2010,46(1):335-348.
[3] CERASOLI C.An analysis of unmanned airborne vehicle relay coverage in urban environments[C].IEEE Military Communications Conference,2007:1-7.
[4] ZHAN P C,YU K,SWINDLEHURST A L.Wireless relay communications with unmanned aerial vehicles: performance and optimization[J].IEEE Transactions on Aerospace and Electronics Systems,2011,47(3):2068-2085.
[5] ZHANG S,LIEW S C,LAM P P.Hot topic:physical-layer network coding[C].ACM MobiCom’06,Calfomia,2006:358-365.
[6] 池新生,郑宝玉,姚刚,等.非对称协作分集通信中网络编码的应用[J].电子与信息学报,2012,34(10):2314-2319.
[7] 魏浩,郑宝玉,侯晓赟,等.不对称速率双向中继传输策略研究[J].电子与信息学报,2012,34(11):2748-2756.
[8] 张祖凡,彭醇陵,杨静,等.基于符号映射的物理层网络编码[J].系统工程与电子技术,2014,36(7):1410-1415.
[9] LI B,WANG G,CHONG P H J,et al.Performance of physical-layer network coding in asymmetric two-way relay channels[J].China Communications,2013(10):65-73.
[10] VAZE R,HEATH R.On the capacity and diversity-multiplexing tradeoff of the two-way relay channel[J].IEEE Transactions on Information Theory,2011,57(7):4219-4234.

