摘 要: 为了标定基于线结构光的三维测量系统中的旋转轴,提出了一种基于圆锥体参照物的快速标定方法。将一个圆锥体的参照物固定放置在旋转平台上,控制旋转台每隔一定角度旋转一次,分别采集每个位置的图像,对图像预处理后,提取圆锥体的亚像素边缘,通过拟合圆锥体边缘直线,计算得到两条边缘直线的空间直线方程,并利用Levenberg-Marquardt迭代法计算出空间中距离两条边缘直线最近的点作为圆锥体的顶点,然后根据得到的所有顶点拟合出所在的空间平面及空间圆的圆心,根据平面的法向量和圆心点建立起旋转轴的直线方程,完成旋转台的转轴标定。实验结果表明,该标定方法具有较高的标定精度。
关键词: 圆锥体;线结构光;旋转台;标定
0 引言
在光学三维测量中,物体表面的测量因其速度快、易于自动化、非接触等优点,在工业检测、考古、生物医学、逆向工程等领域具有非常重要的意义和广阔的应用前景,因此得到越来越多相关领域的广泛关注。在被动式测量中,由于线结构光一次只能得到一条光条,因此为了得到完整的物体表面三维信息还需要进行一维扫描。一般有旋转和平移两种一维扫描方式,若采用旋转式扫描,当旋转台旋转一周之后便可以得到物体整个表面的三维信息。
目前提出的基于线结构光的旋转台转轴标定方法主要有三种:(1)基于标准圆柱体标定转台中心的方法[1],但该方法没有考虑到旋转台与水平面的倾斜角度问题;(2)用标准标定球对转轴进行标定[2];(3)使用棋盘格标定板进行标定转台[3],但该方法没有考虑到当双目相机的有效视场较小时,标定板的旋转角度有限,导致拟合的空间平面误差增大。此外参考文献[4]提出使用多个控制点结合最小二乘法标定转轴,但是没有给出一种有效的求解方法。本文提出一种采用圆锥体对转轴标定的方法,在满足精度要求的前提下,采用加工相对方便且精度符合要求的圆锥体靶标,方法新颖,标定过程简单,算法较易实现。
1 测量系统构成
基于线结构光的三维测量系统主要由线结构光激光器、2台工业相机、电动旋转台、图像采集卡和计算机组成,如图1所示。
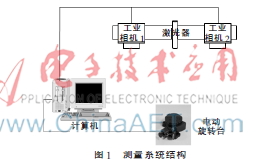
2 基本原理

如图2所示,由于系统装置安装误差,导致了旋转台的转轴方向与平行于世界坐标系Yw的Y′轴方向之间有一定夹角,从而导致测得的物体表面数据不可避免会有一定偏差。因此转台标定是基于旋转台的线结构光三维测量系统的重要一步。
为了能够精确地标定旋转台转轴参数,在旋转台旋转角度已知的前提下,利用Sobel算子和Zernike矩相结合的方法提取圆锥体的亚像素边缘[5]。拟合两条边缘的两条空间直线l1和l2的直线方程,在空间中求取两直线交点P(x,y,z),把P点坐标代入目标函数:

利用Levenberg-Marquardt迭代法[6]求得使目标函数达到最小的点,可以认为P(x,y,z)即为所有的圆锥顶点坐标Pi(xi,yi,zi)。其中d为顶点P到直线l1和l2的距离。最后根据最小二乘法拟合所有顶点所在的空间平面为:
Z=a0X+a1Y+a2(2)
由此可计算空间单位法向量为:
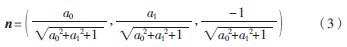
为了在平面上拟合平面圆计算圆心,可以把世界坐标系下的转轴方向向量n(nx,ny,nz)旋转到转台坐标系下,使其与世界坐标系的Yw轴重合,这样在转台坐标系下转轴的方向向量就变为l(0,1,0),可采用罗德里格斯公式计算其绕法向量r(rx,ry,rz)旋转的旋转矩阵R[7],具体公式为:

把所有顶点乘以旋转矩阵R旋转到转台坐标系下后,顶点所在的平面与XOZ平面平行,把这些点投影到XOZ平面后便可根据最小二乘法拟合XOZ平面上的顶点投影所在的平面圆进而得到其圆心O′(x′0,y′0,z′0),然后再把拟合得到的圆心O′逆向旋转回世界坐标系下后得到O0(x0,y0,z0),即可得到旋转轴的全部参数。

得到旋转轴的参数后,计算出转台坐标系与世界坐标系的位置关系如图3所示。首先要计算N轴与Y′轴之间的夹角?渍,然后将N轴投影到XOY平面,计算N轴的投影与X′轴之间的夹角,之后便可以得到N轴绕Z′轴、Y′轴旋转到与XOZ平面平行的旋转矩阵Ry、Rz分别为:
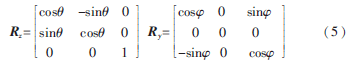
3 实验结果及分析
实验中采用镜头焦距为12 mm、分辨率为1 280×1 024的大恒DH-HV1310Fx型工业相机,线形激光器和大恒GCD-011080M电控旋转台搭建起了基于线结构光的三维扫描系统。根据上述标定原理,对该型号电动旋转台进行标定实验和误差分析。
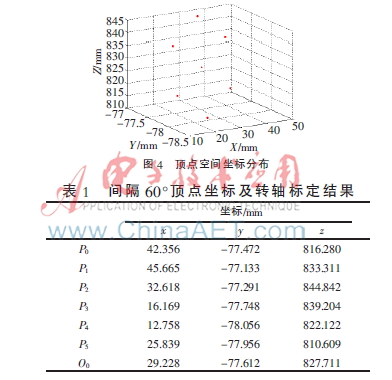
标定使用圆锥体为工厂加工的直径精度为9 m的圆锥工件,将圆锥体固定放置在旋转台上,旋转角度选择每隔60°旋转一次,一共得到6个顶点坐标。图4所示分别为每隔60°圆锥体旋转一周后顶点的三维坐标分布。计算得到旋转轴的方向向量n(nx,ny,nz)和圆心坐标O0(x0,y0,z0)的均值和标准差。其中每隔60°旋转得到的顶点的不同位置坐标及计算得到的圆心坐标如表1所示。
测量点Pi(xi,yi,zi)先通过转轴标定得到旋转矩阵Rz和Ry旋转到转台坐标系下的坐标为P″i(x″i,y″i,z″i),然后绕旋转轴N旋转一定角度α后再通过逆向旋转即可得到点P′i(x′i,y′i,z′i)的坐标,依次把每一组点云数据旋转到不同方位即可得到被测物体的表面三维信息。转台坐标之间的关系为:
![KK([U{ZQ1AYBZCEE3K]1G[P.png KK([U{ZQ1AYBZCEE3K]1G[P.png](http://files.chinaaet.com/images/2016/01/06/6358770809840600004026558.png)
其中,(x0,y0,z0)为转轴上一点即转台中心O0,α是每组点云之间转台旋转的角度,参见图3。同理T-、R-z,R-x向相反的方向旋转即可。
实验中根据标定得到的参数,使用精密圆柱体标准件进行扫描测量,并对测量结果进行了分析比较,圆柱体标准件的直径为24.5±0.01 mm,测量得到的圆柱体拟合直径为24.541 5 mm,测量结果与标准件的直径精度相对一致,距离拟合圆柱体表面最大正向误差为0.118 3 mm,最大负向误差为0.094 7 mm,平均距离误差为0.054 mm。此外将一个茶杯放置在旋转台上,以 0.5°为旋转间隔对其进行扫描测量,得到图5所示滤除掉噪声点的茶杯点云数据及三维重建后的茶杯模型。

4 结论
本文提出的算法通过测量圆锥体参照物在旋转台不同位置的顶点,能够较精确得到转台中心旋转轴的参数,简化了标定过程,标定速度快,易操作。实验结果表明,该方法具有较高的标定精度,具有一定的实用性。其他基于旋转台的三维测量系统都可利用此标定方法对旋转轴进行标定。
参考文献
[1] 周会成,陈洁红,阳道善.一种新型三维视觉测头的结构与原理[J].电子测量与仪器学报,2000,14(2):21-25.
[2] 徐永安,杨钦,怀进鹏.激光旋转扫描测量系统中转轴标定及多视拼合[J].中国激光,2005,32(5):659-662.
[3] 李怀泽,沈会良,程岳.基于旋转多视角深度配准的三维重建方法[J].计算机应用,2012,32(12):3365-3368.
[4] 尹茂东.基于旋转平台的物体表面三维重建研究[D].青岛:青岛大学,2007.
[5] 姜迈,梁晔,梁炜,等.Zernike亚像素图像矩边缘检测算子模型研究[J].计算机测量与控制,2013,21(4):874-876.
[6] LEVENBERG K. A method for the solution of certain nonlinear problems in least squares[J]. Quarterly Applied Mathematics, 1944,2:164-166.
[7] BRADKSI G, KAEBLE A. Learning OpenCV: computer vision with the OpenCV library[M]. Sebastopol, California, USA:O′Reilly Media Inc., 2008.

