摘  要： 通过对上海洋山深水港口的船舶流量的调研以及对船舶交通流量影响因素的分析，建立支持向量机预测模型。同时为了解决支持向量机预测模型的参数选择问题，引入了粒子群优化算法进行参数优化，建立较优的PSO-SVM预测模型。通过MATLAB仿真实验计算，将PSO-SVM模型与单纯的SVM预测模型和灰色神经网络预测模型结果进行对比分析，证明了该模型的可行性和优越性。

　　关键词： 船舶流量；多因素；预测；灰色神经网络；支持向量机；粒子群优化算法

0 引言

　　船舶交通流量预测是将经济预测技术和水运工程技术以及计算机技术有效地结合起来的一门涉及多门学科的新兴应用科学。船舶交通流量的预测相比于一般的市场预测及陆上交通预测等所要考虑的因素和指标要更为繁杂和复杂[1]，对于数据采集处理要求更高，这就要求在运用具体的方法时要因地制宜。其中国内外学者用的较多的是人工神经网络预测法及其组合预测法。但是人工神经网络由于其容易陷入局部最小、预测输出随机等问题，从而降低了预测的精度。

　　支持向量机（Support Vector Machine，SVM）是一种新型的机器学习算法，它同样以统计学理论为基础，以严格的数学理论为背景，因其简单明了的几何解释以及较高的泛化能力，在解决小样本问题时具有独特的优势。于此同时，与人工神经网络相比，其克服了神经网络中经常出现局部最优解以及学习时间长、收敛速度慢等问题。但支持向量机还存在一些不足，如模型的预测精度受训练学习参数选取的影响很大，如何选取参数至关重要。因此，选取合适的参数是支持向量机从理论走向实际应用的关键。本文基于粒子群（Particle Swarm Optimization，PSO）算法的优势，用以对支持向量机难以确定的参数进行优化，进而建立起PSO-SVM预测模型用以上海洋山深水港交通流量的预测。

1 主要影响因素分析

　　船舶交通流量是经济、社会、政治、技术发展对水运交通需求的具体反应。无论选用何种预测方法进行船舶交通流量预测，都必须从实际分析考虑所预测模型的影响因素。影响船舶交通流量的因素非常繁杂，以上海洋山深水港为研究对象，在综合分析和查阅大量文献的基础上，可以从经济因素、港口因素、船舶因素、其他因素四个主要的方面去研究。

　　经济因素是影响未来船舶交通流量的最主要的因素，上海国际航运研究中心将宏观综合的经济指标合理化为上海航运景气指数[2]。船舶的货运量是衡量和量化港口因素的主要指标。同时，伴随着经济贸易和造船技术的发展，船舶越来越向着大型、自动、快速、专业化和标准化的方向发展，考虑到衡量船舶因素的指标有很多，根据实际选择需要选择船舶平均吨位做为合适的指标。另外，经济的变化总能体现在船舶交通流量上，而且呈现正比关系，但是又有一定的滞后性。所以根据实际情况考虑及数据处理的方便，对主要影响因素进行分析抽象、量化后选取上海航运指数、货运量、船舶的平均吨位[3]、七天前的流量4个因素作为主要因素预测上海洋山港船舶交通流量。

2 船舶流量预测模型的构建

　　2.1 建立流量预测模型

　　根据上述主要影响因素构建船舶流量预测算法流程，如图1所示[4-7]。

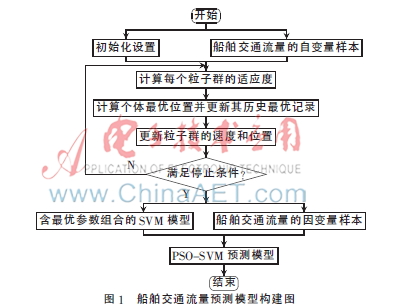
　　2.2 优化支持向量机模型学习步骤

　　PSO优化SVM的学习步骤如下[8]：

　　（1）收集有关影响船舶交通流量的各种数据，分为因变量和自变量样本；初始化各种参数，如粒子群规模、初始位置和速度以及SVM的核函数、惩罚参数等。

　　（2）利用初始化后各粒子的数据值对因变量样本进行学习和训练并建立各自对应的预测模型。

　　（3）通过对因变量样本的学习训练，得到各个粒子的误差值，用以计算各粒子的适应度函数值，公式如下：

　　（4）计算每个粒子的当前适应值F（Xi），并与该粒子当前自身的最优适应值F（Pibest）进行比较，如果F（Xi）<F（Pibest），则调整F（Pibest）=F（Xi），将当前位置作为此刻该粒子的最优位置。

　　（5）将每一个粒子自身当前最优位置的适应值    F（Pibest）与所有粒子当前最优位置的适应值F（Pgbest）进行比较，若F（Pibest）<F（Pgbest），则调整F（Pgbest）=F（Pibest），将调整后的位置做为所有粒子的最优位置。

　　（6）利用PSO的进化方程调整粒子的速度和位置，进而得到支持向量机的参数。

　　（7）判断所有粒子最优位置的适应值或迭代次数能否满足要求，若满足，则停止计算，并保存此时的粒子群的整体最优位置；若不满足，则返回步骤（2）。

　　（8）将最优参数代入支持向量机模型，对样本进行有效预测。

3 仿真实验及结果分析

　　3.1 实验数据及实验设置

　　以上海洋山深水港进出的船舶为研究对象，利用上海国际航运研究中心和上海洋山深水港统计的数据，选取从2014年5月20日~2014年6月29日的船舶交通流量数、当日的上海航运指数、转运量、船舶平均吨位作为自变量，将2014年5月21日~2014年6月30日，当天船舶流量数据作为因变量，建立预测模型对2014年5月21日~2014年6月30日每日的船舶流量数进行回归拟合预测。在实验仿真之前首先得将所采用的流量数据进行归一化处理，采用的归一化处理公式为：

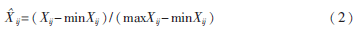
　　式中，j为归一化后的数据；Xij为原始数据；minXij和maxXij分别为原始数据中的最小值和最大值。

　　基于MATLAB语言编写了PSO-SVM程序，通过试算确定PSO的参数如下：粒子个数为20；粒子维数为2；循环次数为200；学习因子c1=1.5，c2=1.7；参数C的搜索范围为（0.1，100）；参数?滓的搜索范围为（0.1，1 000）。经过PSO优化，得到SVM的最优参数C=0.1，利用最优参数来建立SVM模型，进而对测试样本进行预测。

　　3.2 实验仿真对比及分析

　　分别对灰色神经网络模型、SVM模型、PSO-SVM模型进行仿真并对比，仿真结果见图2~图4。

　　对于预测结果需要通过定量的分析以确定精确度，本文采用平均误差和相对百分误差来检验预测结果。预测结果误差如表1所示。

　　从图2~图4中可见，灰色BP神经网络组合预测模型及SVM模型都得到不错的效果，但由于BP神经网络样本有时无法满足要求，存在过拟合现象及SVM参数选择的问题，两种算法的预测结果的准确性都受到很大影响。PSO具有强大的全局搜索能力，通过PSO优化SVM模型的参数，使其达到最优，从而使误差降到最低。

　　从表1可以看出，PSO-SVM预测模型的平均误差和相对百分误差分别为1.653 6%和1.637 8%，明显小于灰色神经网络预测模型和单纯SVM预测模型的预测误差。因此，经PSO优化的SVM模型比神经网络预测模型以及SVM模型具有更好的预测能力。

4 结束语

　　本文在考虑船舶影响因素的条件下，利用SVM预测模型具有小样本学习能力、学习速度快、泛化能力强等优点对船舶流量进行回归预测，并采用PSO优化选择SVM模型的参数，得到较优的SVM模型，从而大大提高了预测的准确性和精度。实验结果表明，基于PSO-SVM的预测模型要好于单纯的SVM预测模型，该模型为船舶交通流量预测提供了新思路及有效方法。

参考文献

　　[1] 陈崇云.我国水上交通运输安全分析及事故预测的研究[D].大连：大连海事大学，2002.

　　[2] 王东，熊锡龙.基于影响因素分析的船舶交通流量预测多元线性回归模型[J].船海工程，2010，39（3）：178-180.

　　[3] 李俊，徐志京，唐贝贝.基于GA优化的灰色神经网络船舶交通流量预测方法研究[J].船海工程，2013，42（5）：135-137.

　　[4] 冯宏祥，肖英杰，孔凡邨，等.基于支持向量机的船舶交通流量预测模型[J].中国航海，2011，34（4）：62-66.

　　[5] 任洪娥，霍满冬.基于PSO优化的SVM预测应用研究[J].计算机应用研究，2009，26（3）：867-869.

　　[6] 王树洋，黄天民，方新，等.基于PSO-SVM的交通流量短时预测[J].重庆交通大学学报（自然科学版），2012，31（4）：832-835，872.

　　[7] 李红喜，付玉慧，张仁初，等.港口船舶交通流量预测[J].大连海事大学学报，2009，35（3）：40-42.

　　[8] 闫冠勇.基于PSO-SVM的CFG桩复合地基质量预测研究[D].邯郸：河北工程大学，2012.