摘 要: 对传统堆排序算法进行分析并做出改进。利用堆的性质降低堆排序过程中的数据比较次数,从而在不提高空间复杂度的前提下改进了堆排序算法的效率。通过理论分析得到改进算法在堆重建过程中的数据比较次数是传统堆排序算法的一半,即改进算法的时间复杂度的主项系数是传统算法的1/2。同时,实验结果表明,改进算法的效率比传统算法提高了20%左右。
关键词: 堆排序;算法;堆重建;数据比较次数;时间复杂度
0 引言
堆实质是一棵完全二叉树,其任何一非叶节点满足性质:(ki≤k2i,ki≤k2i+1)或(ki≥k2i,ki≥k2i+1)(i=1,2,3,4,…,n/2)。利用堆进行排序是一种高效的排序方法,它的时间复杂度为T(n)=2nlog2n+O(n)[1],而且没有什么最坏情况导致堆排序的运行明显变慢,同时它的空间复杂性为O(1)[2]。排序算法的优劣衡量标准主要由排序的时间开销决定,而时间开销主要由数据的比较次数和数据移动次数决定。理论已经推导出该算法的时间复杂度已经到达了比较排序的时间复杂度下限[3],那么只能降低其时间复杂度的主项系数来提高该算法的效率。参考文献[3]改进算法与本文算法有些相似之处,但根据参考文献[3]的实验数据可知其算法的效率提高了10%左右,而本文中效率提高达到了20%左右。王晓东在《最优堆排序算法》一文中并没有给出实验结果,只是从理论上分析了时间复杂度。王珞在《堆排序的推广改进》一文中虽然效率提高较大,但空间复杂度也提高了,算法也比较复杂。为此,本文在保持传统算法优点的前提下提出了一种简单有效的算法来提高效率,并由实验数据证明算法改进的有效性。
1 问题描述
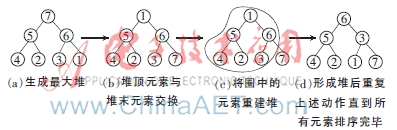
传统的堆排序分为两步:(1)根据初始输入数据,利用堆的调整算法形成初始堆;(2)通过一系列的元素交换和重新调整堆进行排序[2]。排序过程如图1所示。
在上述过程中不难发现:每次形成最大堆后交换堆顶与堆末元素(记为tail),再逐步做下滑调整重建堆。下滑调整的目的是使大数上浮一层(即使较小的数下滑一层),在该算法中每次下调比较次数是2,移动一次数据。在每次交换数据时,把较小的数放到最顶端,使整个序列又处于比较坏的情况,这无疑增加了许多不必要的数据移动。那么能否为这个被交换的元素(tail)找到它合适的位置再插进去?根据堆的性质可以知道:堆顶的元素被移走后,新的堆顶的元素肯定是它的左右子女中较大的一个。可以不交换数据,先将堆末元素取走,把堆顶元素直接放在堆末元素的位置,在它的子女中找到较大的那个子女上移一层,重复这个动作直到叶节点,这样在每一层比较中只需要比较一次。
2 算法思路与描述
2.1 改进的算法思路
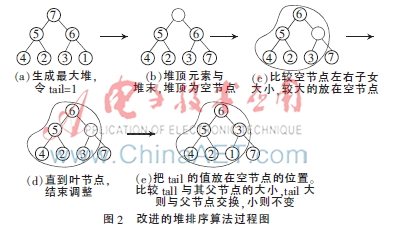
在最大堆生成后,令tail=堆末元素(即先取走堆末元素),堆顶元素放在堆末的位置,则堆顶变为空节点。现在开始把除堆末节点以外的元素重建最大堆,比较空节点左右子女的大小,将较大的那个子女放在空节点的位置,取走的那个子女为新的空节点,重复这个动作直到叶节点。将tail的值填充在空节点。比较原空节点(tail)的值与其父节点的大小,如果父节点较大则不变,反之交换两个元素的值。
改进的堆排序算法过程如图2所示。
2.2 tail位置的确定
在上述过程中,需要证明一个问题,即如何在过程最后只比较一次tail的值与父节点的大小就可确定tail的位置。
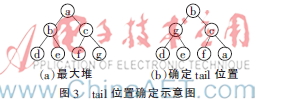
证明过程如下。设图3(a)中的堆为最大堆,则已知:tail=g,c>g,按照上述规则,a放在g的位置,则a为空节点。现在假设b>c,则b>g,那么b放在图3(a)中a节点的位置,d、e中较大的元素放在图3(a)中b节点的位置(设d较大),则现在图3(a)中d节点的位置为空节点,用tail(即g)的值填充。现在比较d与g的大小,若g大则结果如图3(b)所示,是符合最大堆的条件的。将假设设为相反的条件,也是同理。所以只需要比较一次tail的值与父节点的大小即可确定tail的位置。
2.3 算法描述
该算法用C++语言描述,核心代码如下:
template<class T>
void MaxHeap<T>::HeapSort()
{
createMaxHeap(arr);//创建初始堆
T tail=0;
int j=1;
for(int i=currentSize-1;i>=0;i--)
{
if(i<2)
if(heap[0]>heap[1])
{
swap(0,1);
break;
}
int m=0,n=1;
tail=heap[i];//取出堆末元素
heap[i]=heap[0];//堆顶元素放在堆末
while(n+1<i)//重建堆
{
if(heap[n]>heap[n+1])
//找到子女中较大的使其上升
heap[m]=heap[n];
else
{
heap[m]=heap[n+1];
n++;}
m=n;n=2*n+1;//进行下一个子树的重建
}
if(tail>heap[(m-1)/2])//确定tail的位置
{
heap[m]=heap[(m-1)/2];
heap[(m-1)/2]=temp;
}
else heap[m]=tail;}
};
3 算法复杂度分析与结果对比
3.1 数据移动次数计算
本文中初始堆的建立和数据移动次数与传统算法一致,所以在此主要是比较数据的比较次数。设二叉树有n个节点,对应的完全二叉树的深度为k=log2n+1」。每一次堆重建在二叉树的每一层都会比较1次,所以要进行k次比较。在整个过程中需要进行n-2次堆的重建,所以数据需要比较k*(n-2)次,每次确定tail位置需要比较一次,共(n-2)次,在最后还需要加上两个节点的情况,比较2次,所以改进的排序算法数据比较次数为T=nlog2n-2log2n+n。传统堆排序堆重建的最多比较次数为T=2nlog2n+4n+8[1]。通过两种算法相比较可知,改进的堆排序算法的比较次数在主项系数上少了一半。
3.2 实验结果对比
为了证实相应的结论,比较改进的算法与传统算法之间的效率,在VC6.0环境下用rand()函数产生不同量的随机数,用QueryPerformanceFrequency()函数获取算法的计算时间。每组数据是测量的10组数据的平均值,做出两种算法时间的直方图,如图4所示。由图4可知,提高的效率(时间差/传统算法时间)分别为18.4%、14.2%、 21.9%、19.0%、24.2%、18.6%、17.1%、15.1%,平均值为18.6%,所以效率提高了20%左右。
4 结论

通过上述分析,传统的堆排序在堆重建过程中最坏情况下数据比较次数为T=2nlog2n+4n+8,已经达到该类算法时间复杂度数量级下限,因此本文中对算法的改进体现在降低算法中数据比较次数。在理论分析中改进的算法在最坏情况下数据比较次数为T=nlog2n-2log2n+n,可以得到改进算法在主项系数上为传统算法的一半。通过实验结果对比可知,改进算法在效率上提高了20%左右,并且该算法在空间复杂性上依旧为O(1),保持了传统算法的优点,表明该算法的改进是有效的。
参考文献
[1] 卢开澄.算法与复杂性[M].北京:高等教育出版社,1995.
[2] 殷人昆.数据结构(用面向对象方法与C++语言描述)(第二版)[M].北京:清华大学出版社,2007.
[3] 唐开山.堆排序算法研究[J].绍兴文理学院学报,2004,24(10):16-18.

