摘  要： 扩散映射（Diffusion Maps）是一种基于流形学习的非线性降维方法。基于对扩散映射的研究，提出了一种新的非线性降维算法。根据近邻点分布的不同和模糊聚类原理，新算法定义了扩散映射算法构建权值矩阵的误差近似系数，并采用改进的距离公式来选取样本点的近邻点，很大程度地降低了近邻点的选取对降维效果的影响。实验结果表明，新算法有效地保持了高维数据中的流形结构，具有更好的降维效果，并在基于内容的图像检索中达到很高的查准率，新算法的有效性和优越性得到了证实。
　　关键词： 扩散映射；降维；流形学习；聚类
0 引言
　　流形是局部具有欧几里得空间性质的空间，包括各种维数的曲线、曲面等，是一般的几何对象的总称。流形学习[1-3]以流形理论为基础，把高维空间中的样本集在低维空间中重新表示出来，并能求出其相应的嵌入映射，很好地保持了样本点的拓扑结构，达到了维数约简的目的。流形学习方法减少了高维数据的冗余性，解决了维数灾难的问题，因此，流形学习具有非常重要的研究意义。目前，流形学习的方法主要分为两类：一类是线性降维方法，主要有主成分分析（Principal Component Analysis，PCA）[4]、独立分量分析（Independent Component Analysis，ICA）[5]、多维尺度分析（Multidimensional Scaling，MDS）[6]等；另一类是非线性降维方法，主要有核主成分分析（Kernel Principal Component Analysis，KPCA）[7]、等度规映射（Isometric Mapping，Isomap）[8]、局部线性嵌入（Locally Linear Embedding，LLE）[9]等。
　　扩散映射（Diffusion Maps，DM）[10]是COIFMAN R等人在2006年提出的一种基于流形学习的非线性降维方法，其主要思想来自于动力系统。作为一种新的流形学习框架，扩散映射通过在扩散过程中尽可能地保持扩散距离来进行降维，即保持样本点的局部结构不变，通过局部关系定义全局关系，使样本点在低维空间中仍保持这种稳定的全局关系。近邻点选取和分布的不同可产生不同的邻接图，对扩散映射的降维效果影响很大，由此本文提出了一种改进的算法。由于聚类的中心含有大量的信息，新算法根据聚类原理，先定义了扩散映射构建权值矩阵的误差近似系数，然后利用改进的距离函数来选取近邻点，构建邻接图。新算法模糊了近邻点的选取对实验结果的影响，达到了较为理想的降维效果，并在实验中得到了证实。
　　1 Diffusion Maps（DM）算法
　　DM算法主要分为如下4步：
　　（1）构建邻接图。对于给定的数据集X={x1，x2，…，xN}，xi∈RD，i=1，2，…，N，若xi是xj的近邻点，则将xi与xj之间赋一个边，边反映了样本点之间的局部关系，近邻点一般用欧氏距离来度量，距离公式为：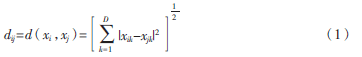
　

　（2）构建权值矩阵W。权值矩阵的元素Wij（W（xi，xj））反映样本点xi与xj之间的相似程度，因此满足：
　　①W是对称的：Wij=Wji；
　　②W是非负的：Wij≥0。
　　一般采用高斯核函数定义成对数据点之间的相似度矩阵，即：

　　其中，为高斯核的方差，越大，权值越大，数据点间的相似程度越大。
　　（3）构建扩散核矩阵K。利用加权的图Laplacian归一化方法。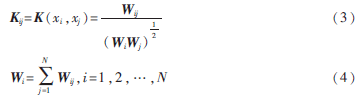

　　其中，Wi表示xi与其他各点的权值之和。
　　（4）核矩阵K的特征分解。对内积矩阵K进行特征分解，求K的特征值和特征向量，K的最大的d个特征值λ1，λ2，…，λd对应的特征向量为U=[u1，u2，…，ud]，则高维数据X降维后的数据集为Y=UT=[u1，u2，…，ud]T。
2 新算法的提出
　　2.1聚类原理
　　聚类是解决高维数据问题的常用方法。聚类分类产生一些簇，簇是一组数据对象的集合，同一簇中的对象相似，不同簇中的对象相异，每个簇的中心含有丰富的可利用的信息，具有代表性。模糊C均值（Fuzzy C-Means，FCM）算法[11-13]是应用最广泛的聚类分析方法之一。
　　对于给定的采样于维流形的高维观测数据集X={x1，x2，…，xN}，xi∈RD，i=1，2，…，D。设样本点聚类分类的类别个数为M，第j类样本的中心为cj，第j类样本的个数为rj，总体样本的中心为c。则定义第j类样本点的类内平均距离为：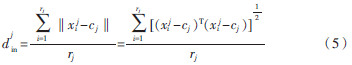

　　第j类样本中心与总体样本中心的距离为：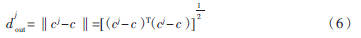

　　其中，‖‖表示欧式距离。由此，定义样本点构建权值矩阵的误差近似系数为：

　　其中，j为样本点xi所属的类。
　　用误差近似系数重新构建样本点在低维空间上嵌入的权值矩阵，从而提高样本点之间的相似程度，获得更好的实验结果。
　　2.2 改进的距离函数
　　对于分布不均匀的数据集，假设P为分布密集的区域上的点，其k个近邻点所占的区域为SP，O为分布稀疏的区域上的点，其k个近邻点所占的区域为SO，显然SP要比SO小得多。因此对于分布不均匀的样本集，近邻点k个数的选取会影响实验结果。所以要对近邻点间的距离进行改进，降低样本点分布的影响。下面定义一种新的距离[14-15]。

　　其中，Gi、Gj分别表示xi、xj和其他点之间距离的平均值。
　　因为新的距离的分子是欧氏距离，分母是数值，则有：
　　①非负性：dij≥0，当且仅当xi=xj，即i=j时等号成立；
　　②对称性：dij=dji；
　　③三角不等式性：dis+dsj≥dij。
　　由泛函分析知识可知，新的距离满足距离空间的定义。在DM的第一步构建邻接图时，采用新的距离公式取代欧氏距离来选取样本点的k个近邻点。新的距离使分布较密集区域的样本点间的距离增大，而使分布较稀疏区域的样本点间的距离缩小，这样区域SP和SO区域的差异性减小，样本点的整体分布趋于均匀化，从而降低样本点的分布对算法效果的影响。
　　2.3改进的算法（Improved Diffusion Maps，IMDM）
　　IMDM算法的步骤如下：
　　（1）对样本集进行聚类分类，得出构建权值矩阵的误差近似系数：

　　（2）构建邻接图。距离公式为：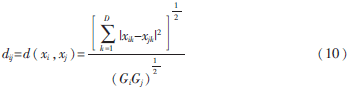

　　（3）构建权值矩阵W′。

　　（4）构建扩散核矩阵K′。

　　（5）核矩阵K′的特征分解。求K′的特征值和特征向量，K′的最大的d个特征值λ′1，λ′2，…，λ′d对应的特征向量为U′=[u′1，u′2，…，u′d]，则高维数据X降维后的数据集为Y=[U′]T=[u′1，u′2，…，u′d]T。
　　新算法首先对样本集进行聚类分类，利用类别信息得出构建权值矩阵的误差近似系数，然后采用新的距离函数选取近邻点构建邻接图，这样可适当降低近邻点个数k的选取对算法的影响，得到较好的降维效果。
3 实验结果及分析
　　3.1人工数据
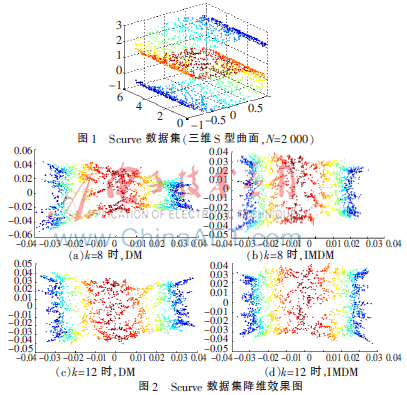
　　用DM和IMDM对Scurve人工数据集（如图1所示）进行降维，实验选取2 000个样本点，近邻点的个数分别取8、12，将数据集降至2维，实验结果如图2所示。从图2中可以看出，IMDM比DM具有更好的降维效果，模糊了近邻点个数的选取，降维效果比较理想，具有更好的可视化效果。

　　3.2 图像检索
　　在基于内容的图像检索实验中，图像选自Corel数据库，共1 000幅图像，类别为10种，有建筑、风景、人物、动物、植物等。实验对第450号恐龙图像进行相关图像检索，降至维数d分别取6、14、20，检索出的图像数目设为20。实验一先用DM方法对图像数据集降维然后进行检索，得出实验结果如图3中的（a）、（c）、（e）所示。实验二先用IMDM方法对图像数据集降维再进行检索，得出实验结果如图3中的（b）、（d）、（f）所示。对比两次实验结果，可以清晰地看出，IMDM降维后进行基于内容的图像检索的准确率明显高于DM的。

　　查准率是衡量图像检索算法有效性的常用指标，查准率越高，表示图像检索方法越好，反之越差。

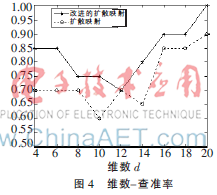
　　图4为在维数不同时，DM和IMDM查准率的变化情况。可以看出，多数情况下IMDM降维后图像检索的查准率高于DM的。特别地，当维数为20时，应用IMDM方法，查准率达到了100%。

4 结论
　　本文对基于流形学习的扩散映射非线性降维方法进行了分析研究，提出了一种改进的扩散映射非线性降维方法。此方法以聚类分类原理构造权值矩阵的误差近似系数，通过改变样本点间的距离公式重新构建邻接图，进而实现降维。新算法有效地降低了近邻点的选取对降维效果的影响，并且很好地保留了原始数据的拓扑结构。将改进的扩散映射方法用于Scurve数据集和基于内容的图像检索实验，都得到了很好的效果，具有很好的实际应用价值。
　　参考文献
　　[1] ORSENIGO C， VERCELLISN C. Kernel ridge regres-sion for out-of-sample mapping in supervised manifold learning[J]. Expert Systems with Application， 2012，39（9）：7757-7762.
　　[2] 曹林林.基于流形学习的分类技术[D].济南：山东师范大学，2013.
　　[3] 王自强，钱旭，孔敏.流形学习算法综述[J].计算机工程与应用，2008，44（35）：9-12.
　　[4] 曾宪华，罗四维.全局保持的流形学习算法对比研究[J].计算机工程与应用，2010，46（15）：1-6.
　　[5] HYVARINEN A， OJA E. Independent component analysis：algorithms and applications[J]. Neural Networks， 2000，13（45）： 411-430.
　　[6] COX T， COX M. Multidimensional scaling[M]. London：Chapman&Hall， 1994.
　　[7] SCHOLKOPF B， SMOLA A， MULLER K R. Nonliner co- mponent analysis as a kernel eigenvalue problem[J]. Neural Computation，1998，10（5）：1299-1319
　　[8] THEODORIDIS S，KOUTROUMBAS K.模式识别（第4版）[M].李晶皎，王爱侠，王骄，等译.北京：电子工业出版社，2010.
　　[9] Zhang Zhenyue， Zha Hongyuan. Principal manifold and nonlinear dimensionality reduction via local tangent space alignment[J]. SIAM Journal of Scientific Computing， 2004，26（1）：313-338.
　　[10] COIFMAN R， LAFON S. Diffusion maps. Applied and computational harmonic analysis[EB/OL]. [2006-05-30].http： www.elsevier.com/locate/acha.
　　[11] 姜伦，丁华福.关于模糊C-均值（FCM）聚类算法的改进[J].计算机与数字工程，2010，38（2）：4-6.
　　[12] 苏锦旗，张文宇.基于模糊聚类的改进LLE算法[J]，计算机与现代化，2014，225（5）：9-13.
　　[13] BEZDEK J C， EHRLICH R. Full W. FCM： the fuzzy c-means clustering algorithm[J]. Computers & Geosciences，1984，10（2）：191-203.
　　[14] 王和勇，郑杰，姚正安.基于聚类和改进距离的LLE方法在数据降维中的应用[J]，计算机研究与发展，2006，43（8）：1485-1490.
　　[15] JOSHUA B T， VIN.DE S， LANGFORD J C. A global geometric framework for nonliner dimensionality reduction[J]. Science， 2000，290：2319-2323.