摘  要： 车辆导航系统的核心是路径规划算法，路径规划算法分静态路径规划（Static Path Planning， SPP）算法和动态路径规划（Dynamic Path Planning， DPP）算法，SPP的不足是不能对实时变化交通信息做出快速响应，而DPP则可以利用路网中实时更新的交通信息及时地为驾驶者提供更佳的导航路线。本文在研究了静态路径规划中用到的一些算法后，如A*算法，继而分析动态路径规划的一些思想，在此基础上分析D*Lite算法可以改进的地方，并给出优化后的算法程序。利用10×10、50×50、100×100三种规模的模拟路网做对比实验，实验表明优化后的D*Lite算法在速度上有了较大提高。

　　关键词： 动态路径规划；A*；D*；LPA*；D*Lite

0 引言

　　生成导航路径的算法有多种，其中经典算法之一便是Dijkstra算法[1]，该算法也是其他众多算法的基础。为提高求解最优路径的效率，研究者们相继提出了多种快速算法，其中A*算法[2-3]是其中较重要的一种算法，它采用启发式搜索的方式，不再像Dijkstra算法盲目式搜索，可使搜索范围明显缩小，也使导航效率得到提高；双向搜索（Bidirectional Search）[4]也是一种快速搜索方式，它采用从起点和目标点同时开始搜索的策略，理想情况下会在路径的中点处相遇，从而终止搜索过程；分层技术（Hierarchical Methods）[5-6]采用预处理的办法使待搜索的路网维度降低，从而达到快速搜索的目的。

　　交通信息是动态变化的，如某个路段此时拥堵，或畅通，或限行等，在下一时刻此路段信息可能又发生了变化，为应对这种情况，当需要为驾驶者及时更新导航路径时，简单重复调用静态导航算法并不是最优的选择。Anthony Stentz在1994年提出了D*（Dynamic A*）[7-8]算法，即动态A*算法，该算法的最初目的是解决机器人在不确定环境下的寻路问题。Koenig和Likhachev在2004年提出LPA*算法[9]，该算法受人工智能领域的“增量搜索”（Incremental Search）思想启发，通过复用先前搜索产生的信息，从而达到可以快速重新规划最优路径的目的。LPA*算法解决的是定起点、定目标点的寻路问题，为应对变起点、定目标点问题，Koenig和Likhachev在LPA*算法的基础上又提出了D*Lite[10]算法。2011年K Al-Mutib等人又将D*Lite算法应用于多机器（Multi-Agent）的实时动态路径规划[11]。本文通过对D*Lite算法分析，发现该算法在执行过程中有些计算是可以避免的，从而可以使算法效率更高。

1 A*算法

　　A*算法的核心在于估价函数的设计上，如式（1）所示：

　　f（n）=g（n）+h（n）（1）

　　其中g（n）称为耗散函数，表示从起始节点nstart到节点n的实际代价；h（n）称为启发函数，表示节点n到目标节点ngoal的估计代价；f（n）表示从起始节点经由节点n到目标节点的估计代价。

　　同Dijkstra算法类似，A*算法也维持一个Open表。Open表中节点的优先级是依据f（n）的大小排列的，   f（n）值越小，被搜索到的优先级越高。为保证能搜索到最优解，启发函数h（n）不能太大，不能大于节点n到目标节点的实际代价；但如果h（n）=0，则A*算法退化为Dijkstra算法，虽能保证得到最优路径，但算法效率低；如果h（n）恰好等于节点n到目标节点的实际代价，则A*算法探索的节点恰好就是最优路径上的节点。所以h（n）的取值直接影响算法的速度和精确度，常见的   h（n）的取值有两点之间的欧几里得距离（Euclidean Distance）和曼哈顿距离（Manhattan Distance）等。

　　图1所示为h（n）的大小对搜索空间的影响对比图。

2 D*Lite算法

　　D*Lite算法是Koenig S和Likhachev M在LPA*算法的基础上提出的。LPA*算法，即Lifelong Planning A*算法，基于A*算法和Dynamic SWSF-FP算法[12]的思想，可以在环境变化时快速求得最优路径。但LPA*算法是为求解定起点和定终点之间最优路径问题而设计，不适用于像车辆导航这种车辆位置变化的情景。为此，Koenig S和Likhachev M通过对LPA*算法改造，使LPA*算法的思想能应用到诸如车辆动态导航这样的问题。

　　LPA*算法区别于其他算法的一个重要特点是rhs（v）的定义，如式（2）：

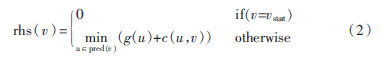
　　其中pred（v）表示节点v的前继节点，g（u）是节点u到起始节点vstart的代价，类似于A*算法中的g（n），c（u，v）表示从节点u到节点v的代价。对于节点v，如果   g（v）=rhs（v），则称该节点“连续”（Consistent），否则称“不连续”（Nonconsistent）。当所有节点连续时，说明g（v）真实代表节点v到起始节点的代价。

　　D*Lite算法继承了rhs（v）的概念，但D*Lite算法是从目标节点向起始节点搜索，这一点和D*算法相同，和LPA*、A*算法相反，此时rhs（v）的定义如式（3）：

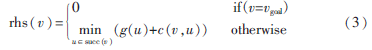
　　succ（v）表示节点v的后续节点，此时g（u）表示节点u到目标节点到代价。D*Lite和LPA*算法的不同之处还在于当环境变化后，节点的启发函数值的处理。如前所述，LPA*算法解决的是起点固定、目标点固定的最优路径搜索问题，节点v的启发函数值不是动态变化的；然而，D*Lite算法面向的是起点（如车辆位置）随时间变化、目标点固定的最优路径搜索问题，节点v的启发函数值是随着起点位置的变化而变化的。为此，Koenig S和Likhachev M在参考文献[11]中给出了两种解决方法：一是，根据新的起点位置，将优先队列（Priority queue）中所有节点的启发函数值重新计算；二是，并不重新计算队列中的启发函数值，而是在计算新添加到优先队列中的节点的启发函数值时，加上一个修饰符km，km表示车辆或机器人移动距离的叠加。

3 D*Lite Label算法

　　通过分析D*Lite算法，发现该算法仍然存在一些可以改进的地方。

　　（1）初始化时无需对网络中所有节点都进行初始化，因为采用启发式搜索，有些节点根本就不会被搜索到。

　　（2）在判断某节点是否存在于优先列表中时，如果遍历整个表，则效率并不是最优的。

　　（3）在更新节点v的rhs（v）时，在某些情况下并不需要探索它的所有后继节点。如果v是连续节点，它的某个后继节点u触发了v的更新程序，此时只需比较rhs（v）和g（u）+c（v，u）的大小。

　　（4）当路径规划结束后，机器人或车辆要向下一个节点运动时，D*Lite算法采用贪婪搜索的方式寻找下一个节点。令u表示当前节点v的一个后继节点，如果g（u）+c（v，u）最小，则该后继节点就是下一步要移向的节点。该策略仍然需要探索当前节点的所有后继节点。

　　针对上述问题，参考D*算法的设计，本文采用为节点设置标号v.Tag的方式和父节点属性v.Father的方式进行优化。为区别经典D*Lite算法，本文将下述算法定义为D*Lite Label算法。

　　定义有向图G=（V，E），其中V表示节点集合，E表示边的集合，e（u，v）∈E表示有向边u→v，c（u，v）表示e（u，v）的权值，限定c（u，v）≥0。Succ（v）表示节点v的后继节点集合，u∈Succ（v）表示存在有向边e（v，u）；Pred（v）表示节点v的前续节点集合，u∈Pred（v）表示存在有向边e（u，v）。为节点v设置父节点属性v.Father，如果v.Father=u，则表示在最优路径上v的下一节点是u。类似于A*算法中的Open表和Close表，D*Lite算法用一个优先队列Queue来保存等待更新的节点，本文仍然沿用优先队列Queue这个概念。另外，本文还为每个节点v设置标号v.Tag属性，如果v.Tag=NEW，则表示该节点还未曾被搜索到；如果v.Tag=OPEN，则表示该节点等待更新且已存入Queue队列中；如果v.Tag=CLOSED，则表示该节点已经从Queue中移除。用v.g、v.rhs、v.h分别代表D*Lite算法中的g（v）、rhs（v）、h（vstart，v）。

　　先对程序进行初始化，StartV表示车辆起始位置节点，GoalV表示目标节点。

　　Initial（）{

　　L1/StartV.rhs=StartV.g=∞；GoalV.rhs=0；

　　L2/GoalV.Tag=OPEN；Queue.Add（GoalV）；

　　L3\}

　　程序运行中，Queue.Top（）函数返回Queue中Key值最小的节点，Key的取值与D*Lite算法一致，Key=[min（v.g，v.rhs）+v.h+km，min（v.g，v.rhs）]，函数Cal_Key（v）用于计算节点v的Key值。CurrV表示车辆当前位置节点。Stentz在参考文献[7]描述D*算法时将节点状态分为两类，一类处于“下降状态”（LOWER state），一类处于“上升状态”（RAISE state）。针对两种状态节点，本文创新性地采用两种更新策略。当TopV.g>TopV.rhs时，节点处于下降状态，调用Update_Lower（u，SourceV）函数对TopV的前续节点进行更新，u表示待更新节点，SourceV表示触发u被更新的源节点；当TopV.g<TopV.rhs时，节点处于上升状态，调用Update_Raise（u）对TopV的前续节点进行更新。

　　ComputeShortestPath（CurrV）{

　　L1/   TopV=Queue.Top（）；

　　L2/   while（TopV.Key<CurrV.Key

　　L3/        ||CurrV.rhs!=CurrV.g）{

　　L4  if（TopV.g>TopV.rhs）{

　　L5/        TopV.g=TopV.rhs；

　　L6/        TopV.Tag=CLOSED；Queue.Remove（TopV）；

　　L7/        for all u∈Pred（TopV）

　　L8/    Update_Lower（u，TopV）；}

　　L9/   else{

　　L10/ TopV.g=∞；

　　L11/ for all u∈Pred（TopV）

　　L12/ Update_Raise（u）；}

　　L13/   TopV=Queue.Top（）；

　　L14\   } }

　　Update_Lower（u，SourceV） {

　　L1\ switch （u.Tag）{

　　L2/ case NEW：

　　L3/  u.rhs=SouceV.g+c（u，SourceV）；Cal_Key（u）；

　　L4\   u.Father=SouceV； u.Tag=OPEN； Queue.Add（u）；

　　L5/ case OPEN：

　　L6/  if（u.rhs>SourceV.g+ c（u，SourceV）） {

　　L7/    u.rhs=SourceV.g+ c（u，SourceV）；

　　L8\    u.Father=SouceV； Cal_Key（u）；}

　　L9/ case CLOSED：

　　L10/  if（u.rhs>SourceV.g+ c（u，SourceV）

　　L11/    ||u.Father=SourceV）{

　　L12/  u.rhs=SourceV.g+ c（u，SourceV）； Cal_Key（u）；

　　L13/  u.Father=SouceV；u.Tag=OPEN；Queue.Add（u）；}

　　L14\ } }

　　Update_Raise（u） {

　　L1\ if（u!=GoalV）{

　　L2/ for all v∈Succ（u）{

　　L3/  if（v.Tag==CLOSED&&u.rhs>v.g+c（u，v））{

　　L4/   u.rhs=v.g+c（u，v）；u.Father=v；}

　　L5/  }

　　L6/ if（u.rhs!=u.g && u.Tag!=OPEN） {

　　L7/   u.Tag=OPEN； Cal_Key（u）；Queue.Add（u）； }

　　L8/ if（u.rhs==u.g&&u.Tag==OPEN） {

　　L9/   u.Tag=CLOSED；Queue.Remove（u）；}

　　L10/ } }

　　程序运行的主程序同D*Lite算法基本一致，稍微不同的一点是，当最后更新节点时需判断该节点是处于上升状态还是下降状态，然后采用相应的更新函数，主程序其余部分此处不再赘述，请见参考文献[11]。

4 实验结果

　　本文分别采用10×10、50×50、100×100的方阵图模拟路网，每条边代表一条路，每条边的权值为1~5之间的均匀随机整数，起始点和目标点为网络中的交叉点，位置随机决定。启发函数采用两点之间的曼哈顿距离。当起始点和目标点的位置确定后，分别用A*算法、D*Lite、D*Lite Label三种算法规划最优路径。

　　（1）为模拟车辆位置的动态变化，本文在先前规划好的路径上，产生一个随机位置作为车辆当前位置。

　　（2）为模拟路网环境的变化，本文在车辆当前位置和目标节点之间的路径上产生一个随机“阻塞”，置该条边的权值为无穷大。

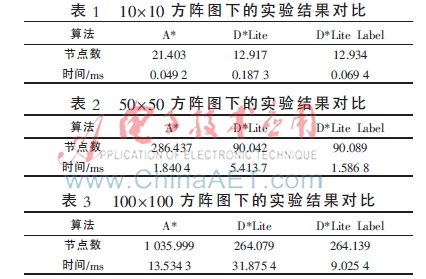
　　当阻塞发生后，分别采用A*、D*Lite、D*Lite Label三种算法对路径重新规划，统计每种算法所探索的节点数、所用时间。本文的A*算法同样采用了标号的方式。在三种规模的路网下做1 000次实验，统计其平均值，实验环境为Intel i5 CPU，主频2.6 GHz，8 GB内存，仿真平台为Visual Studio 2010，得到的实验结果如表1、表2、表3所示。

5 结论

　　实验结果显示，随着路网规模的增大，动态路径规划算法与静态路径规划算法的重复调用相比，其优势更加突出。D*Lite Label算法基于D*Lite算法的思想，在所探索的节点数方面，两种算法基本一致。由于D*Lite Label算法为每个节点增加了一些属性，避免了某些节点被反复更新，且同时使更新过程更加快速，使得该算法在时间效率上更优。

参考文献

　　[1] DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik， 1959， 1（1）： 269-271.

　　[2] NILSSON N J. Principles of artificial intelligence[M]. Berlin：Springer： 1982.

　　[3] HART P E， NILSSON N J， RAPHAEL B. A formal basis for the heuristic determination of minimum cost paths[J]. Systems Science and Cybernetics， IEEE Transactions on， 1968， 4（2）： 100-107.

　　[4] LUBY M， RAGDE P. A bidirectional shortest-path algorithm with good average-case behavior[J]. Algorithmica， 1989，4（1-4）：551-567.

　　[5] SCHULZ M H F， WAGNERT D. Engineering multi-level overlay graphs for shortest-path queries′[C]. Proceedings of the Eighth Workshop on Algorithm Engineering and Experiments and the Third Workshop on Analytic Algorithmics and Combinatorics， SIAM， 2006：123-156.

　　[6] SANDERS P， SCHULTES D. Algorithms-ESA 2006[M]. Berlin Heidelberg Springer， 2006.

　　[7] STENTZ A. Optimal and efficient path planning for partially-known environments[C]. Robotics and Automation， 1994. Proceedings of 1994 IEEE International Conference on. IEEE， 1994： 3310-3317.

　　[8] STENTZ A. The focussed D^* algorithm for real-time replanning[C]. IJCAI. 1995， 95： 1652-1659.

　　[9] KOENIG S， LIKHACHEV M， FURCY D. Lifelong planning A*[J]. Artificial Intelligence， 2004， 155（1）： 93-146.

　　[10] KOENIG S， LIKHACHEV M. Fast replanning for navigation in unknown terrain[J]. Robotics， IEEE Transactions on， 2005，21（3）： 354-363.

　　[11] AL-MUTIB K， ALSULAIMAN M， EMADUDDIN M， et al. D* Lite based real-time multi-agent path planning in dynamic environments[C]. Computational Intelligence， Modelling and Simulation （CIMSiM）， 2011 Third International Conference on. IEEE， 2011： 170-174.

　　[12] RAMALINGAM G， REPS T. An incremental algorithm for a generalization of the shortest-path problem[J]. Journal of Algorithms， 1996， 21（2）： 267-305.