0 引言

    信源定位是阵列信号处理的一个重要研究方向，现代科学技术正在蓬勃发展，定位技术更是广泛应用在航空航天、交通、勘探、导航等领域^[1-2]。例如，军工应用中，雷达需要定位技术作为新的补充，只需利用传感器接收到的信号即可确定目标的位置，而且在定位过程中受到的干扰和攻击可降低到最低水平。因此，信源定位技术因其诸多优点及广泛的应用前景成为学者们的研究重点。

    现在常用的信源定位方法主要分成三类：(1)利用时延估计进行定位^[3]，先进行阵元间时间差的计算，再根据阵列结构与信源模型估计出信源的位置。该定位方法计算量较小，易于实时实现，但仅在单信源定位中得到了广泛的应用。(2)利用波束形成法进行定位^[4]，无需计算时间差，需要通过优化目标函数来实现信源定位，但是实际应用环境中会出现多个最优值即伪峰，所以峰值搜索过程较为复杂。(3)利用高分辨空间谱估计进行定位^[5-6]，可同时高分辨率地定位多个声源，但是对实验环境要求较高。目前大多定位算法都是以窄带信号为研究对象提出的。宽带信号中含有较大带宽和多个中频，直接使用窄带信号对应算法时造成的相位差无法忽略，因此针对宽带信号中的信号频率也有处理方法。文献[7-8]已将最大似然法（ML）扩展至宽带信号处理中，但是由于涉及到高度非线性化及非凸性和最大化似然函数，其计算复杂度较高。另一类是Kaveh在1985年提出的具有高分辨DOA估计的相干信号子空间法(CSSM)[9-11]，通过引入“聚焦”思想，使得不同频率上的观测值全部变换到确定频率上，后对各聚焦后信号的协方差矩阵进行平均，得到聚焦后的协方差矩阵，最后获得宽带信号的高分辨DOA估计，但该方法估计性能易受信源方位预估精度的影响。本文提出了一种针对宽带信源定位的联合质心收缩与联合可控响应功率和相位变换(SRP-PHAT)的信源定位方法^[4，12]，根据对宽带信源获得的DOA估计，利用本文提出的算法构建出信源所在的初始区域，通过质心收缩、布置虚拟信源点等方法逐步收缩区域，最终获得信源定位估计。

1 分布式阵列模型与信号模型

    本文提出的宽带信源定位方法采用的分布式阵列系统由四个均匀线阵组成，如图1所示。

    K个均匀线阵任意分布在分布式系统中，放置于水平面上，且每个线阵含有N个传感器，第i个信源所在位置坐标为(x_si，y_si，z_si)，第k个线阵中心坐标为(x_k，y_k，z_k)，第k个线阵对第i个信源的方位角为θ_ik，由于各线阵是任意分布，故线阵中心连线围成一任意多边形区域V，信源可分布在该多边形区域内的任意位置。

导向矢量α_k(f_j，θ_M)可表示为：

    假设噪声为高斯白噪声，且与各信号均相互独立。阵列流型矩阵可表示为：

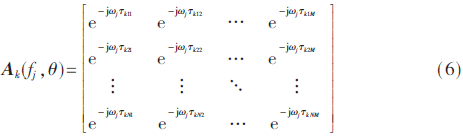
2 信源定位方法

2.1 DOA估计

    DOA估计是信源定位方法的关键步骤，是信源定位确定初始区域的关键。传统的MUSIC算法对常见的阵列都普遍适用，故传统MUSIC算法的空间谱估计公式可定义为：

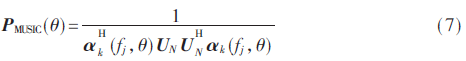
式中U_N则是N×(N-M)噪声子空间。

    由于宽带信号中有多个中心频率，故需将不同中心频率的信号子空间映射到一个最佳的聚焦频率f₀，通过式（8）选取最佳聚焦频率：

    通过谱峰搜索在空间谱P_MUSIC(f₀，θ)中得到。但是，对于密集信源来说，使用传统MUSIC算法进行DOA估计性能较差，而且在少量传感器时甚至无法区分出信源的数目。为提高密集信源的DOA估计精度，本文引入了MUSIC空间谱的群延迟函数来提高密集声源在少量传感器时DOA估计的精度。Group Delay函数利用了MUSIC空间谱相位信息的负差分形式，用其与MUSIC空间谱函数以乘积的形式来消除群延迟谱的伪峰，提高DOA估计精度。Group Delay谱定义为：

其中Φ(f₀，θ)为MUSIC空间谱相位信息，表示为：

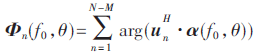
    对P_MGD(f₀，θ)进行谱峰搜索后可得到精确的DOA估计值。

2.2 构建初始区域及质心收缩

    根据式(11)得到的各子阵的DOA估计值、第k个子阵中心的坐标A_k=(x_k，y_k)和第i个信源对第k个子阵的DOA估计值θ_ki，利用点斜式方程，做出一条子阵中心出发的平面射线。所有子阵做出的直线围成一个初始区域，各子阵中心连线与各射线交于一点B_ki=(x_ki，y_ki)，则各射线的交点I_kp=(I_x，I_y)即A_k B_ki与A_p B_pi的交点可通过式(12)、式(13)计算为：

    所有的交点I_kp均保存在集合I中，所有的交点的横纵坐标的最大值和最小值可构成初始区域V₁。通过I中所有交点的坐标可以计算出两两交点之间的相对距离，并找出最大相对距离D_max，而且D_max是随集合I的变化而变化。

    根据I中的交点，计算初始区域的质心：

其中|I|代表集合I中交点的数目。同时可计算出各交点到区域质心的欧几里得距离，表示为：

其中s代表维数，D={D_k}。根据得到的欧几里得距离，找出最小距离对应交点将其插入到新集合P_j中，并从集合I中删除。然后再计算集合P_j中交点所围成区域的质心Cent(P_j)，同时计算出集合I中剩余交点到质心Cent(P_j)的欧几里得距离：

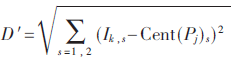
根据上述得到的最大相对距离D_max和集合I、P_j，同时找出集合D′中的最小值min(D′)。将min(D′)与D_max进行比较，当min(D′)≤D_max时，将D′中最小距离对应交点插入到集合P_j中，同时将该点从集合I中删除。重复上述质心收缩步骤，直到min(D′)>D_max时，停止迭代。最后，更新后的集合P_j中的所有交点的横纵坐标最值[x_max  x_min  y_max  y_min]围成粗略收缩区域V₂。

2.3 最大互功率谱收缩定位法

    本节介绍利用SRP-PHAT在区域V2中随机布置虚拟信源点进行区域收缩。首先将联合可控功率函数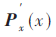定义为：

τ(x，k)为信号从信源沿着得到的DOA估计值到第k个线阵的到达时间长度。由于各虚拟信源点的坐标均已知，可通过虚拟信源点到第k个线阵中心的距离d_k和信号传播速度c获得时间延迟τ(x，k)，即：

    本文的信源定位算法由DOA估计、区域质心收缩和最大互功率谱收缩组成。定位算法步骤如下：

    (1)由式（11）获得的DOA估计值和各线阵中心得到各线阵到信源的射线。

    (2)根据式（12）、式（13）获得各射线直接的交点。

    (3)根据式（14）、式（15）和min(D′)≤Dmax获得最终更新后的交点集合P_j。

    (4)P_j中交点围成了区域V₂。

    (5)在V₂中随机布置虚拟信源点，再根据式（16）计算各虚拟信源点到各线阵的互功率谱。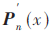

    (6)找出前E个最大互功率谱值对应点，创建新的收缩区域V₃。

    (7)重复步骤(5)和步骤(6)，直到满足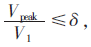然后计算V_peak中虚拟信源点坐标平均值即得到信源定位估计值。

3 仿真实验和分析

    实验仿真证明了本文所提算法的良好性能，图1为实验采用的分布式阵列。各子阵均是采用四个阵元的均匀线阵，线阵中心连线围成了一个4.6 m×5 m的矩形区域，且密集信源在该矩形区域内部，信源1坐标为(2.95 m，2.95 m)，信源2坐标为(1.2 m，3.45 m)，用*代表信源。图中子阵1的中心坐标为A₁=(0 m，0 m)，子阵2、子阵3及子阵4的中心坐标分别为A₂=(5 m，0 m)、A₃=(5 m，4.6 m)、A₄=(0 m，4.6 m)。其中子阵1水平放置，并以其中心坐标为坐标原点，即α=0°；子阵2相对于子阵1逆时针旋转了45°，即β=45°；子阵3相对于子阵1逆时针旋转了90°，即γ=90°；子阵4相对于子阵1逆时针旋转了30°，即η=30°。本文使用实际录音信号为实验的声源信号,声音持续时间为3 s。

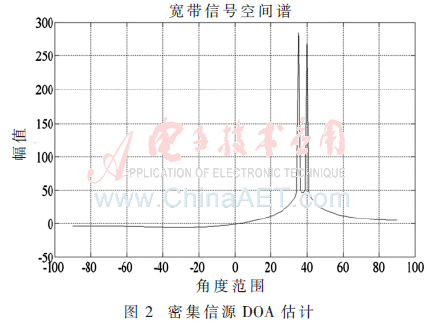
    实验对虚拟信源点数F取值为100，最大互功率谱值对应点数E取值为10。门限值δ取值为1%。根据密集信源位置，图1中两信源对应子阵1中心的角度值为35°和40°，利用CSSM和Group Delay谱的方法对这两个信源进行DOA估计，其谱估计如图3所示，所用噪声为高斯白噪声，信噪比SNR为5 dB。由图2可知，本文使用的DOA估计算法分辨率较高。

    根据前面得到的密集信源的DOA估计值，以声源1为例，利用各子阵中心点和对应DOA估计值作出相应射线，射线所围成的区域即为初始搜索区域，如图3所示。

    根据确定的初始区域，利用质心收缩和最大互功率谱收缩逐步缩小区域，图4（a）是两密集信源的区域收缩过程，其中实线代表信源1的收缩过程，虚线代表信源2的收缩过程。图4（b）则是对图4（a）中圈中区域的细节放大图。图中两实心点为信源位置估计。

    为了对本文算法性能进行评估，提出了位置估计的均方差（RMSE）随信噪比变化的评估方法。本次实验共做200次蒙特卡罗实验，其中RMSE定义为：

4 结束语

    本文着重讨论了二维空间中宽带信号的信源高精度DOA估计和信源定位方法。首先，利用Group Delay函数和CSSM算法对传统MUSIC算法的空间谱加以优化，消除无用伪峰，提高宽带信号的DOA估计精度。利用获得的DOA估计值确定初始搜索区域，然后在二维平面中使用质心收缩和最大互功率谱收缩法对初始区域逐步收缩，得到最终信源的定位估计。本文提出的算法计算简单便捷，仅需DOA一个参数即可获得信源的定位估计。仿真实验结果证明了本文算法的DOA估计精度较高，SNR对信源定位估计的RMSE的影响较小。但是本文算法较为依赖DOA估计确定的初始区域，DOA估计精度的大小直接影响到算法的运算量，可以考虑引入其他参数来控制DOA精度导致的算法计算量过大的问题。

参考文献

[1] 殷晴青，何培宇.相干语音信号的两阵元DOA估计新算法[J].信号处理，2013，29(9)：1169-1175.

[2] 宁强，方向，潘俊，等.圆形传感器阵列多运动声源二维波达方向估计[J].解放军理工大学学报：自然科学版，2013，14(3)：283-287.

[3] OMOLOGO M，SVAIZER P.Use of the crosspower-spectrum phase in acoustic event location[J].IEEE Transactions on Speech & Audio Processing，1997，5(3)：288-292.

[4] DIBIASE J H.A high-accuracy, low-latency technique for talker localization in reverberant environments[D].Brown University，2000.

[5] 居太亮，彭启琮，邵怀宗，等.基于任意麦克风阵列的声源二维DOA估计算法研究[J].通信学报，2005，26(8)：129-133.

[6] CHEN J C，YAO K，HUDSON R E.Acoustic source localization and beamforming：theory and practice[J].Eurasip Journal on Advances in Signal Processing，2003(4)：359-370.

[7] DORON M，WEISS A J，MESSER H.Maximum-likelihood direction finding of wide-band sources[J].IEEE Transactions on Signal Processing，1993，41(1)：411-414.

[8] CHEN J C，HUDSON R E，YAO K.Maximum-likelihood source localization and unknown sensor location estimation for wideband signals in the near-field[J].IEEE Transactions on Signal Processing，2002，50(8)：1843-1854.

[9] KHAN M A，RAO R K，WANG X.Performance of quadratic and exponential multiuser chirp spread spectrum communication systems[C].Performance Evaluation of Computer and Telecommunication Systems(SPECTS)，2013 International Symposium on.IEEE，2013：58-63.

[10] YOON Y S，KAPLAN L M，MCCLELLAN J H.TOPS：new DOA estimator for wideband signals[J].IEEE Transactions on Signal Processing，2006，54(6)：1977-1989.

[11] 张小飞，汪飞，徐大专.阵列信号处理的理论和应用[M].长沙：国防工业出版社，2010.

[12] ASTAPOV S，BERDNIKOVA J，PREDEN J S.A method of initial search region reduction for acoustic localization in distributed systems[C].Mixed Design of Integrated Circuits and Systems(MIXDES)，2013 Proceedings of the 20th International Conference.IEEE，2013：451-456.

[13] KUMAR L，TRIPATHI A，HEGDE R M.Robust multisource localization over planar arrays using music-group delay spectrum[J].IEEE Transactions on Signal Processing，2014，62(17)：4627-4636.